
Удивительный квадрат

Цель работы
- Показать, насколько удивительна такая простая фигура как квадрат.
- Показать разнообразие применения квадрата через решение различных задач.

Общее представление
Как всем давно известно:
- квадрат – это прямоугольник, у которого две смежные стороны равны
- ромб, у которого все углы прямые.

История
Квадрат, как и любая геометрическая фигура, имеет свою историю.. В древнем мире квадрат обычно означает четыре стороны света. И в Ассирии, и в древнем Перу четыре стороны света, четыре направления, то есть квадрат это и есть Весь Мир. Греки описали его силами математики, хотя Пифагор считал все четные числа женскими и слабыми, квадрат же равно как и цифра четыре в силу их делимости и превращения ни во что были описаны лишь отрицательными характеристиками.

Магические квадраты
Сумма чисел в каждом вертикальном и горизонтальном рядах и по каждой из диагоналей одна и та же.
Подмагическими будем понимать квадраты, в которых суммы чисел, стоящих в любом столбце или в любой строке, а также по диагоналям, одинаковы.

Квадрат Пифагора
Квадрат Пифагора – это очень мощный аналитический инструмент. Он позволяет выявить основные особенности личности, обусловленные датой рождения.
Пифагор изучил в Египте, а потом привез в Европу цифровые матрицы, известные ранее только узкому кругу избранных. В адаптированном варианте тайные таблицы дошли до наших дней и ныне известны как квадрат Пифагора.

Квадрат в квадрате
У квадрата, вписанного в квадрат, есть некоторые особенности.

Совершенное квадрирование
Это задача о составлении квадрата из нескольких квадратов, но на этот раз без разрезания их на части и усложнённая ещё требованием, чтобы стороны квадратов выражались неповторяющимися целыми числами. Число данных квадратов безразлично.

Латинские квадраты
Латинский квадрат n-го порядка — таблица L=(lij) размеров n × n, заполненная n элементами множества M таким образом, что в каждой строке и в каждом столбце таблицы каждый элемент из M встречается в точности один раз. Пример латинского квадрата 3-го порядка:
В настоящее время в качестве множества M обычно берётся множество натуральных чисел {1,2,…,n} или множество {0,1,…,n-1}, однако Леонард Эйлер использовал буквы латинского алфавита, откуда латинские квадраты и получили своё название. Латинские квадраты существуют для любого n.

Квадрат Малевича
Квадрат Малевича. Одна из самых известных картин, которая «прославляет» квадрат. Казалось бы, что может быть проще: на белом фоне черный квадрат. Любой человек, наверное, может нарисовать такое. Но вот загадка: черный квадрат на белом фоне - картина русского художника Казимира Малевича, созданная еще в начале века, до сих пор притягивает к себе и исследователей, и любителей живописи.

Оригами
- Базовая форма "дверь". Разверните.
- Сложите верхний правый и нижний левый уголки "долиной".

- Сложите боковые стороны к центральной линии.
- Перегните заготовку по указанным линиям, а потом разверните.

- Заправьте нижний правый угол в карман.
- Заправьте верхний левый угол в карман.
- Вот что получилось. Переверните.

- Соедините нижний и верхний правые углы и верхний и нижний левые углы. Переверните.
- На получившейся заготовке есть два кармана и две вставки. Чтобы собрать кубик, нужно сделать еще 5 таких заготовок, а потом их собрать.

- Так соединяются две заготовки.
- Вот что получилось. Третий модуль нужно вставить в указанный на рисунке карман.

- Вот что получилось. Теперь необходимо соединить еще 3 заготовки.
- Кубик готов. Раскрасьте его грани яркими красками.
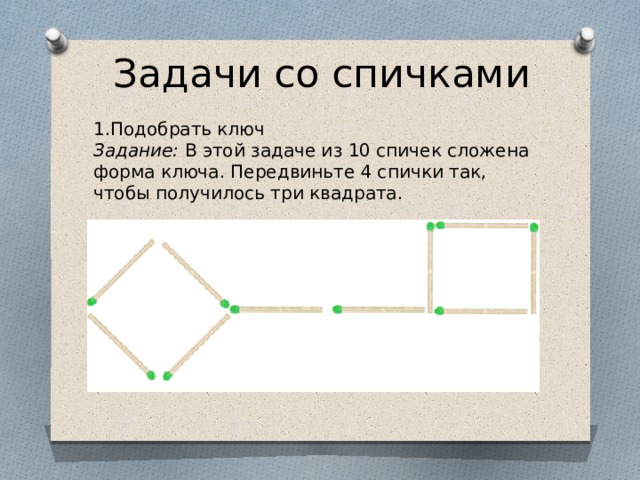
Задачи со спичками
1.Подобрать ключ
Задание: В этой задаче из 10 спичек сложена форма ключа. Передвиньте 4 спички так, чтобы получилось три квадрата.

Ответ. Задача решается достаточно просто. Четыре спички, образующие ту часть ручку ключа, нужно переместить на стержень ключа, так чтобы 3 квадрата были выложены в ряд.
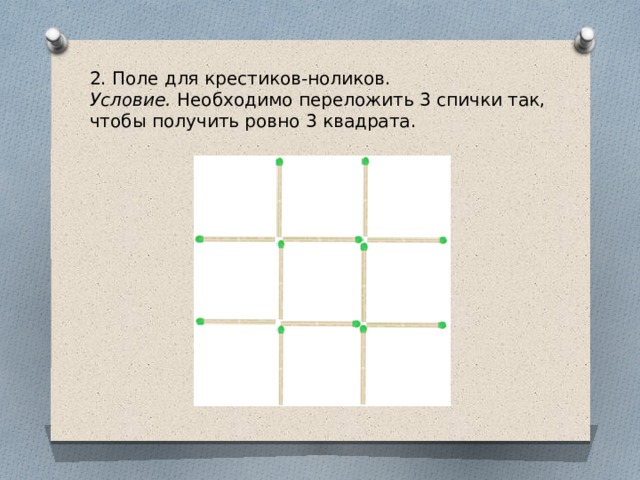
2. Поле для крестиков-ноликов.
Условие. Необходимо переложить 3 спички так, чтобы получить ровно 3 квадрата.

Ответ. Чтобы получить ровно три квадрата в этой задаче необходимо переместить 2 нижних вертикальных спички вправо и влево соответственно, чтобы они замыкали боковые квадраты. А нижней центральной горизонтальной спичкой нужно замкнуть верхний квадрат.

3. Пять из девяти
Условие. Перед Вами девять маленьких квадратов, образованных двадцатью четырьмя спичками. Уберите 8 спичек, не трогая остальных, чтобы осталось всего лишь 2 квадрата.

Ответ. Для этой задачи я нашел 2 способа решения.
Первый способ. Убрать спички так, чтобы остался только самый большой квадрат, образованный крайними спичками и самый маленький квадрат в центре, состоящий из 4 спичек.

Второй способ. Также оставить самый большой квадрат из 12 спичек, а также квадрат 2 на 2 спички. У последнего квадрата 2 стороны должны образовываться спичками большой квадрата, а 2 другие стороны должны быть в центре.

Вывод
Мы показали, насколько удивительна такая простая фигура как квадрат.








































