Презентация к уроку алгебры по теме "Алгебраическая дробь. Допустимые значения переменных, входящих в алгебраические выражения." (8 класс)

Алгебраическая дробь. Допустимые значения переменных, входящих в алгебраические выражения.

Подготовила:

учитель математики

МБОУ Г.ГОРЛОВКИ «ШКОЛА № 42

Рыбина М.В.

Повторим!

Числовые выражения содержат числа, знаки действий и скобки.

При выполнении действий числового выражения по порядку, можно найти число, называемое значением выражения.

Выражение не имеет значения, если содержит деление на ноль.

Если числовое выражение содержит ещё и буквы (или только буквы), обозначающие числа или переменные, то оно называется алгебраическим выражением.

Алгебраическое выражение, в котором есть сложение, умножение, деление и возведение в степень (натуральное число), называется рациональным алгебраическим выражением.

Если рациональное алгебраическое выражение не содержит операции деления на выражение с переменными, то оно называется целым.

Если при составлении рационального алгебраического выражения используется операция деления на выражение с переменными, то такое выражение называется дробным.

Определение

Дробное рациональное выражение, числителем и знаменателем которого являются многочлены, называется  алгебраической дробью.

Примеры

При каких значениях переменной имеет смысл выражение:

Пример 1

Пример 2

Пример 3

Проверь себя!

Проверь себя!

Проверь себя!

-60,5

Проверь себя!

8

-13

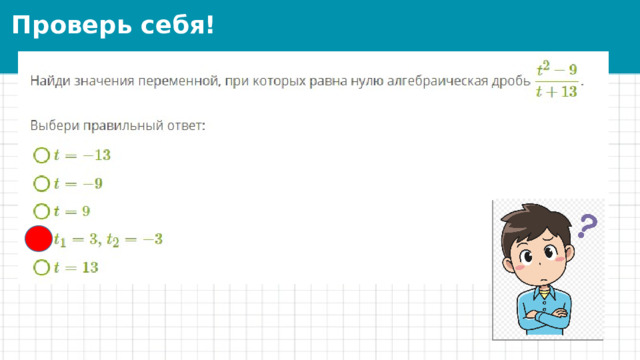
Проверь себя!

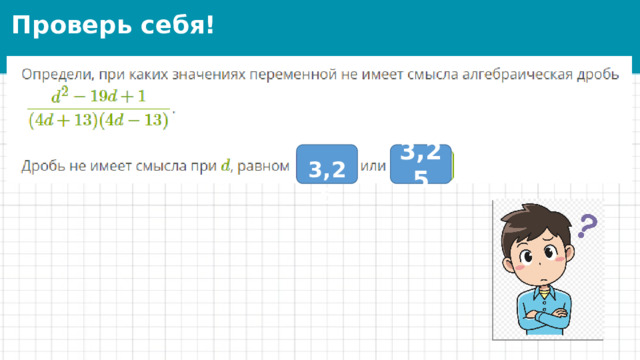
Проверь себя!

- 3,25

3,25

Проверь себя!

-

7

Проверь себя!

Домашнее задание

Выучить определения § 1, п. 1

Выполнить в тетради № 4, 6, 12

Использованные источники:

• https://resh.edu.ru/subject/lesson/1261 /
• https://www.yaklass.ru/p/algebra/8-klass/algebraicheskie-drobi-arifmeticheskie-operatcii-nad-algebraicheskimi-drobi_- 9085/poniatie-algebraicheskoi-drobi-11009
• https:// foxford.ru/wiki/matematika/algebraicheskaya-drob-sokrashcheniye-algebraicheskikh-drobey
• https:// skysmart.ru/articles/mathematic/oblast-dopustimyh-znachenij-funkcii