Презентация к уроку алгебры по теме "График функции. Свойства функции, их отображение на графике" (8 класс)

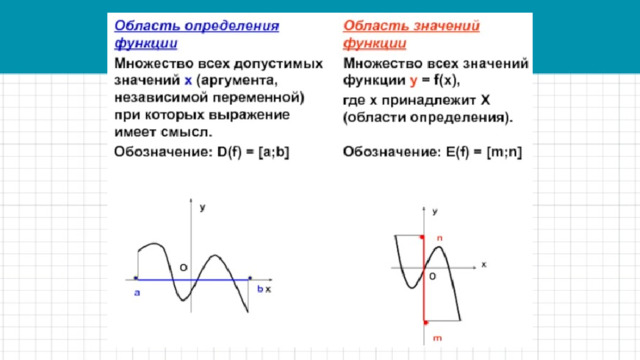
График функции. Свойства функции, их отображение на графике

Подготовила:

учитель математики

МБОУ Г.ГОРЛОВКИ «ШКОЛА № 42

Рыбина М.В.

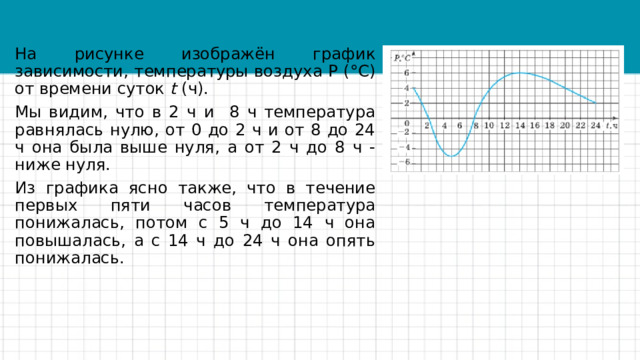
На рисунке изображён график зависимости, температуры воздуха Р (°С) от времени суток t (ч).

Мы видим, что в 2 ч и 8 ч температура равнялась нулю, от 0 до 2 ч и от 8 до 24 ч она была выше нуля, а от 2 ч до 8 ч - ниже нуля.

Из графика ясно также, что в течение первых пяти часов температура понижалась, потом с 5 ч до 14 ч она повышалась, а с 14 ч до 24 ч она опять понижалась.

Рассмотрим теперь свойства функции у = f(x).

Область определения этой функции

D(y) = [-5; 9]

Множество значений функции E(y) = [-4; 5]

Выясним, при каких значениях х функция обращается в нуль, принимает положительные и отрицательные значения.

• Найдем абсциссы точек пересечения графика с осью х. Получим х = -3 и х = 7.

Значит, функция принимает значение, равное нулю, при х = -3 и х = 7

Значения аргумента, при которых функция обращается в нуль, называют нулями функции .

Нули функции разбивают её область на три промежутка [-5; -3), (-3; 7), (7; 9].

Для значений х из промежутка (-3; 7) точки графика расположены выше оси х, а для значений х из промежутков [-5; -3) и (7; 9] – ниже оси х.

Значит, на промежутке (-3;7) функция принимает положительные значения, а на промежутках [-5; -3) и (7; 9] – отрицательные значения.

Промежутки, на которых функция сохраняет знак, называются промежутками знакопостоянства.

Выясним теперь, как изменяются значения функции (увеличиваются или уменьшаются) с изменениями х от -5 до 9.

С возрастанием х от -5 до 3 значения у увеличиваются, а с возрастанием х от 3 до 9 значения у уменьшаются.

Говорят, что на промежутке [-5;3] функция у(х) возрастает, а на промежутке [3; 9] она убывает.

Промежутки возрастания и убывания функции называются промежутками монотонности функции.

Функция называется возрастающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции.

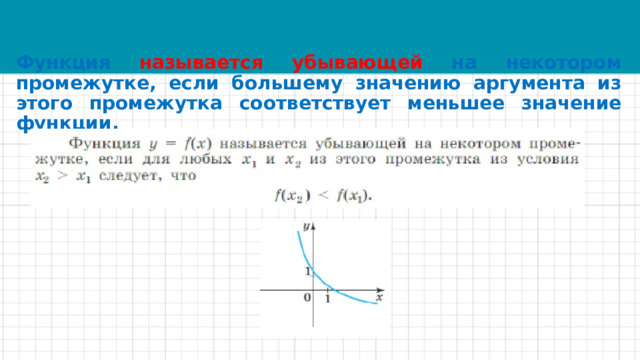
Функция называется убывающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Пример 1. Установите по графикам количество нулей функции

Пример 2. Найдите нули функции

Пример 3

Найдем промежутки знакопостоянства функции

f ( x ) = -2 х + 6

Решение

Для этого решим неравенства:

• -2 х + 6  0, -2 х  -6, х  3

• -2 х + 6  0, -2 х  -6, х  3

Ответ: y  0 при x  (3; +  ),

y  0 при x  (-  ; 3)

Пример 4. Определите промежутки монотонности по графику функции

Функция y = f ( x ) возрастает на промежутках, выделенных на рисунке зеленым цветом, то есть при x  [-9; -8], [-6,5; 1,5], [6; 9].

Функция y = f ( x ) убывает на промежутках, выделенных на рисунке желтым цветом, то есть при x  [-8; -6,5], [1,5; 6].

Пример 5

Подчеркните возрастающие функции красной чертой, а убывающие функции синей чертой.

f ( x ) = 27 – 23 х,

f ( x ) = 3 х,

f ( x ) = – 2 х,

f ( x ) = 2 х + 5,

f ( x ) = ,

f ( x ) =

Задание 1

По графику функции найдите:

а) область определения;

б) множество значений;

в) нули функции;

г) промежутки знакопостоянства функции;

д) промежутки монотонности функции;

е) наименьшее и наибольшее значение функции

Задание 2

Найдите нули функции

Задание 3

Найдите промежутки знакопостоянства функции f ( x ) = 17 – 2 х

Домашнее задание

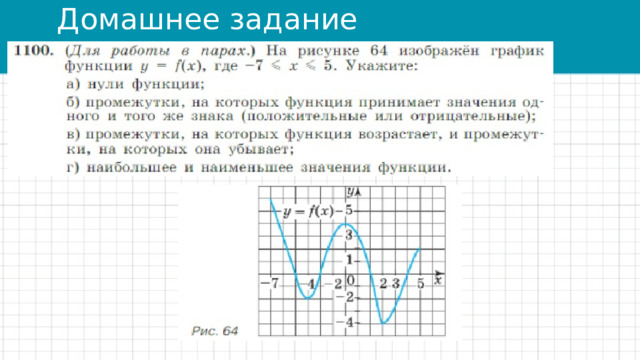
Домашнее задание

Домашнее задание