Презентация к уроку алгебры в 7 классе по теме "Линейная функция, её график и свойства."

Линейная функция, её график и свойства.

Подготовила:

учитель математики

МБОУ Г.ГОРЛОВКИ «ШКОЛА № 42

Рыбина М.В.

Введение

Рассмотрим задачу. За первый час рабочий сделал 3 детали, а за каждый следующий – по 2 детали. Сколько деталей изготовит рабочий через  t  часов?

Запишем функцию:

f(t ) = 3 + 2( t  – 1)

Упростим:

f(t)  = 3 + 2( t  – 1) = 3 + 2 t  - 2 = 2 t  + 1

Функция похожа на прямую пропорциональность, но «мешает» 1! Следовательно, функция похожа, но не является прямой пропорциональностью.

У таких функций есть своё название – линейные.

Об этих функция сегодня и пойдёт разговор. Дадим определение линейной функции.

Определение

Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа.

При этом k — угловой коэффициент , b — свободный коэффициент.

Пример 1

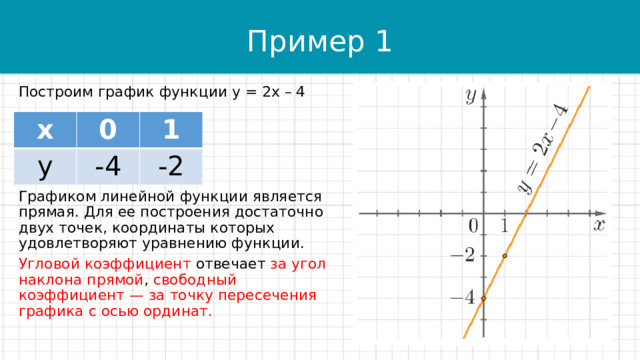
Построим график функции у = 2х – 4

Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.

Угловой коэффициент отвечает за угол наклона прямой , свободный коэффициент — за точку пересечения графика с осью ординат.

х

0

у

1

-4

-2

Чтобы найти точку пересечения с осью х (у = 0), мы приравниваем выражение kx + b к нулю.

kx + b = 0, kx = b, х = - Получаем точку с координатами (-;0)

Чтобы найти точку пересечения с осью у (х = 0), мы подставляем в у = kx + b х = 0.

у = k  0 + b = b. Получаем точку с координатами (0; b).

Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.

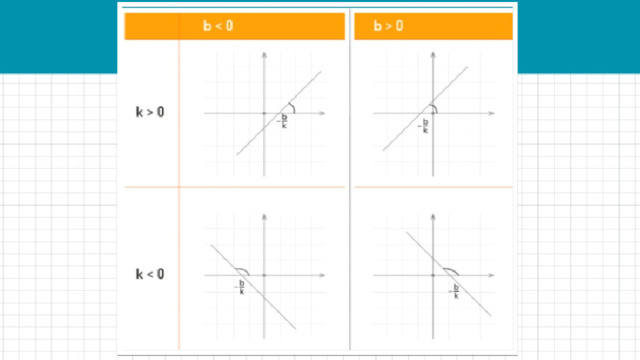
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.

Свойства линейной функции

• Область определения функции — множество всех действительных чисел.
• Множеством значений функции является множество всех действительных чисел.
• График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
• Функция не имеет ни наибольшего, ни наименьшего значений.
• График функции пересекает оси координат:

ось абсцисс ОХ — в точке (-; 0);

ось ординат OY — в точке (0; b).

0 функция принимает отрицательные значения при х  - и положительные значения при х  -.   7. При k " width="640"

Свойства линейной функции

6. При k 0 функция принимает отрицательные значения при х  - и положительные значения при х  -.

7. При k

Частный случай

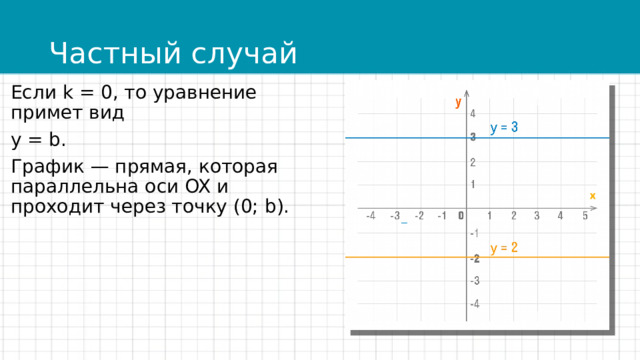
Если k = 0, то уравнение примет вид

y = b.

График — прямая, которая параллельна оси OX и проходит через точку (0; b).

Частный случай

Если b = 0, то уравнение примет вид y = kx. Такая функция называется прямой пропорциональностью.

График — прямая, которая проходит через начало координат.

Пример 1

Начертим три графика функции:

y = 2x + 3;

y = x + 3;

y = x + 3.

Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая. В каждой функции

b = 3, поэтому все графики пересекают ось OY в точке (0; 3).

Пример 2

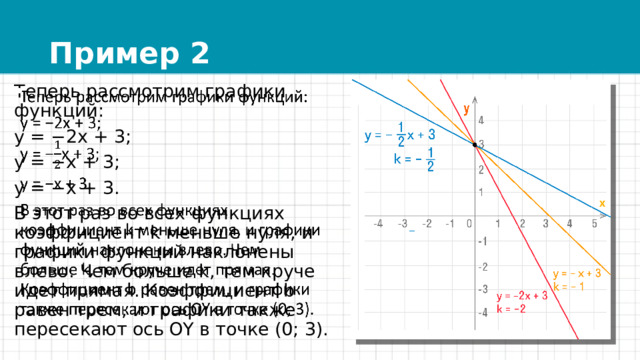
Теперь рассмотрим графики функций:

y = −2x + 3;

y = −x + 3;

y = −x + 3.

В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая. Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).

Пример 3

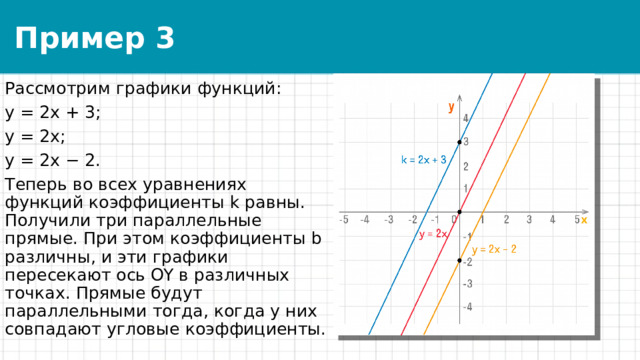
Рассмотрим графики функций:

y = 2x + 3;

y = 2x;

y = 2x − 2.

Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые. При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках. Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.

Задание 1

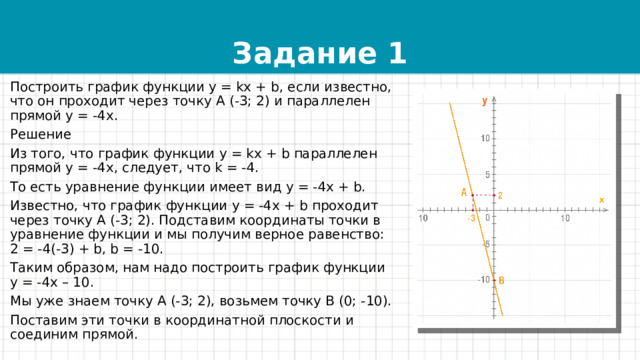
Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.

Решение

Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4.

То есть уравнение функции имеет вид y = -4x + b.

Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство: 2 = -4(-3) + b, b = -10.

Таким образом, нам надо построить график функции y = -4x – 10.

Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).

Поставим эти точки в координатной плоскости и соединим прямой.

Задание 2

Не выполняя построения, найдите координаты точек пересечения с осями координат графика функции у = -5х + 2

Решение

Пересечение с осью х: у = 0

-5х + 2 = 0, -5х = -2, х = 0,4

(0,4; 0)

Пересечение с осью у: х = 0

у = -5  0 +2=2

(0;2)

Ответ: (0,4; 0), (0; 2)

Задание 3

Найдите координаты точки пересечения графиков функций: у = -5х + 16 и у = 2х – 5.

Решение

-5х + 16 = 2х – 5,

-5х – 2х = -5 – 16,

-7х = -21,

х = 3

у = -5  3 + 16 = 1

Ответ: (3;1)

Проверь себя!

Проверь себя!

Длина прямоугольника  x  см, а ширина на 2 см меньше. Задайте формулой зависимость периметра от его длины. Является ли получившаяся функция линейной?

Проверь себя!

Какие из данных функций является линейной?

Проверь себя!

  Укажите цвет графика, который задан формулой:  y  = – x  + 3.

Проверь себя!

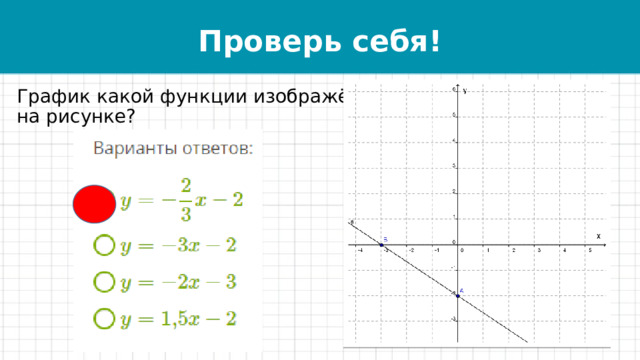
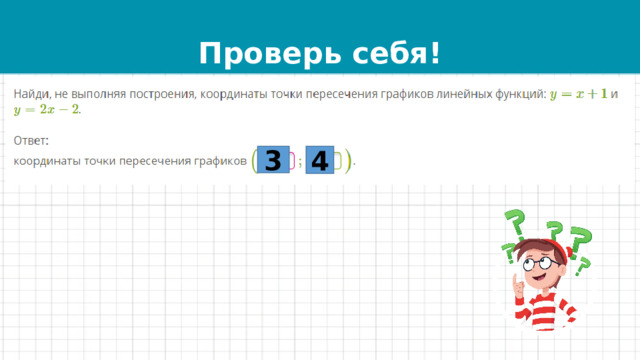
График какой функции изображён на рисунке?

Проверь себя!

-9,35

Проверь себя!

10

Проверь себя!

Каждую секунду в ванну из крана поступает 0,2м 3  воды. Сколько кубометров воды станет в ванне через  x  секунд, если сейчас в ней уже 20м 3 . Задайте формулой зависимость объёма воды в ванне от времени её наполнения.

Ответ: V = 0,2x + 20

Проверь себя!

У воспитателя было 50 мандаринов. Он раздал их  x  детям по две штуки каждому. После этого у него осталось  y  мандаринов. Задайте формулой зависимость  y  от  x .

Ответ: y = 50 - 2x

Проверь себя!

-12

Проверь себя!

1

-6,1

3,3

8,7

12,3

Проверь себя!

0

-10

Проверь себя!

6

0

Проверь себя!

линейной

прямая

-3

b =

2

k =

Проверь себя!

3

4

Проверь себя!

-3

Проверь себя!

1,6

1,6

Рефлексия

Домашнее задание

Выучить определения § 6, п. 16

Выполнить в тетради № 317, 319 (а),

322 (а), 324 (а, б)

Использованные источники:

• https://resh.edu.ru/subject/lesson/1340 /
• https:// www.yaklass.ru/p/algebra/7-klass/lineinaia-funktciia-y-kx-m-9165/lineinaia-funktciia-y-kx-m-grafik-lineinoi-funktcii-9107/re-6bf40f08-aae0-443f-b0ec-de161575f7ee
• https:// skysmart.ru/articles/mathematic/grafik-linejnoj-funkcii
• https:// foxford.ru/wiki/matematika/linejnaya-funkciya-ee-svojstva-i-grafik
• https:// www.evkova.org/funktsiya