Презентация к уроку алгебры "Возведение в квадрат и в куб суммы и разности двух выражений" (7 класс)

Возведение в квадрат и в куб суммы и разности двух выражений

Подготовила:

учитель математики

МБОУ Г.ГОРЛОВКИ «ШКОЛА № 42»

Рыбина М.В.

Квадрат суммы

Используем правило умножения многочленов

( a + b ) 2 = ( a + b )( a + b ) =

= a 2 + ab + ab + b 2 = a 2 + 2 ab + b 2

Итак!

Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второе плюс квадрат второго

( a + b ) 2 = a 2 + 2 ab + b 2

Квадрат разности

Используем правило умножения многочленов

( a - b ) 2 = ( a - b )( a - b ) =

= a 2 - ab - ab + b 2 = a 2 - 2 ab + b 2

Итак!

Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второе плюс квадрат второго

( a - b ) 2 = a 2 - 2 ab + b 2

Куб суммы

Используем правило умножения многочленов.

( a + b ) 3 = (( a + b )( a + b ))( a + b ) =

= ( a 2 + ab + ab + b 2 )( a + b )=

= ( a 2 + 2 ab + b 2 )( a + b ) =

= a 3 + a 2 b + 2 a 2 b + 2 ab 2 + b 2 a + b 3 =

= a 3 + 3 a 2 b + 3 ab 2 + b 3

Итак!

Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.

( a + b ) 3 = a 3 + 3 a 2 b + 3 ab 2 + b 3

Куб разности

Используем правило умножения многочленов.

( a - b ) 3 = (( a - b )( a - b ))( a - b ) =

= ( a 2 - ab - ab + b 2 )( a - b )=

= ( a 2 - 2 ab + b 2 )( a - b ) =

= a 3 - a 2 b - 2 a 2 b + 2 ab 2 + b 2 a - b 3 =

= a 3 - 3 a 2 b + 3 ab 2 - b 3

Итак!

Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго.

( a - b ) 3 = a 3 - 3 a 2 b + 3 ab 2 - b 3

Задание 1

Представьте в виде многочлена: (a + 2b) 2  

Решение

Применяем формулу квадрат суммы.

(a + 2b) 2  =  a 2  + 2  a  2b + (2b) 2 = 

= a 2  + 4ab + 4b 2

Задание 2

Представьте в виде многочлена:

( 2a – 5b) 2

Решение

( 2a – 5b) 2  = (2 a) 2  – 2  ⋅  2a  ⋅  5b + (5b) 2 =

= 4a 2  – 20ab +25b 2

Задание 3

Найдите куб двучлена:

• (a + 3) 3  = a 3  + 3a 2  · 3 + 3a · 3 2  + 3 3  =

= a 3  + 9a 2  + 27a + 27 .

• (10 – a) 3  =10 3  – 3 · 10 2  a + 3 · 10 · a 2  – a 3  =

= 1000 – 300a + 30a 2  – a 3 .

Задание 4

Упростите: x 3  + 3x(x + 4) – (x + 2) 3

x 3  + 3x 2  + 12x – (x 3  + 6x 2  + 12x + 8) =

= x 3  + 3x 2  + 12x – x 3  – 6x 2  – 12x – 8 =

= -3x 2  – 8 .

Ответ:   -3x 2  – 8 .

Задание 5

Решите уравнение:

x 3  + 9x 2  – (x + 3) 3  = 0

x 3  + 9x 2  – (x 3  + 9x 2  + 27x + 27) = 0

x 3  + 9x 2  – x 3  – 9x 2  – 27x – 27 = 0

-27x = 27

Ответ: х = -1.

Проверь себя!

Преобразуйте квадрат двучлена в многочлен стандартного вида.

Проверь себя!

Упростите выражение и выберите получившийся ответ из списка.

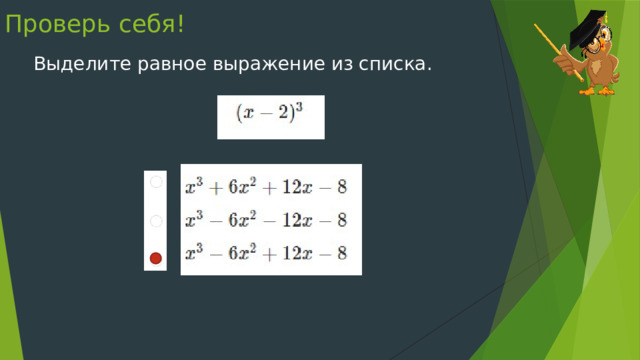
Проверь себя!

Выделите равное выражение из списка.

Проверь себя!

Проверь себя!

Найдите корень уравнения

x 3 + 3 x 2 + 1 – x 3 – 3 x 2 – 3 x – 1 = 0,

-3 x = 0,

x = 0

Ответ: 0

Домашнее задание

Читать § 12, п. 32

Выполнить в тетради № 803, 827, 828

Использованные источники:

https:// www.evkova.org/formulyi-sokraschennogo-umnozheniya

https://uchitel.pro/ формулы-сокращенного-умножения /

https:// skysmart.ru/articles/mathematic/formuly-sokrashennogo-umnozheniya

https://resh.edu.ru/subject/lesson/7247/conspect/292432 /

https://resh.edu.ru/subject/lesson/1138 /