Презентация к уроку "Функция y=sin x. Свойства и график функции"

Свойства и график функции y=sin x

Устная разминка

4

1

2

3

sin90°

cos90°

cos180°

√ 2/2

1

0

sin(π/4)

-1

8

6

7

5

√ 3/2

sin(π/ 3)

sin270°

cos360°

√ 3/2

1

-1

cos(π/6)

11

12

9

10

cos(2π)

cos(‒π)

ctg(π/6)

1

-1

-1

sin(3π/ 2)

√ 3

☺

14

15

13

0

1/2

cos(-π/ 2)

cos(π/3)

tg(π/4)

1

Молодец!

Назовите функции, графики которых изображены на рисунке.

Построение графика y = sin x

График функции y = sinx можно получить сдвигом графика функции у= cosх вдоль оси абсцисс вправо на единиц

π

2

p

y = cosx

y = cos(x - )

y = = sinx

2

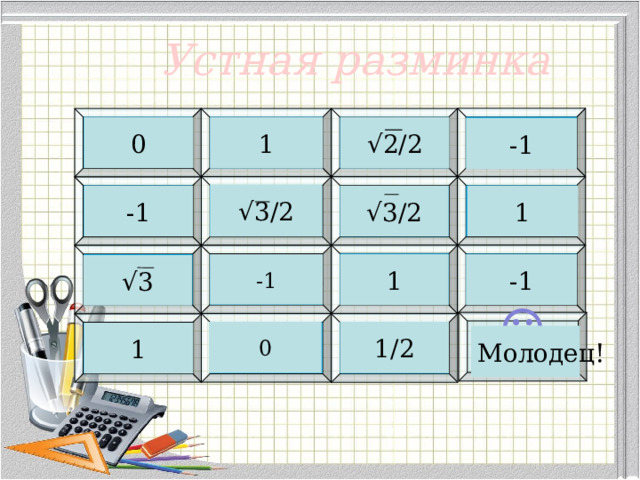
Множество значений

Область определения

Нечётная

, график симметричен относительно начала координат

Основные свойства функции у=sinx

- множество R всех действительных чисел

- отрезок [-1; 1]

, Т=2π

Периодическая

Нули функции:

У=0 при х=πk, k ϵ Z

y

1

p

- p

5p

- 3p

3p

- 5p

-2π

-π

2π

π

2

2

0

2

2

2

2

x

-1

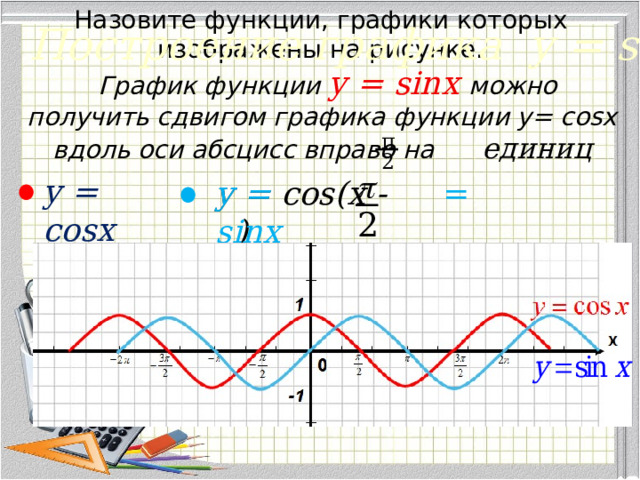
Функция убывает

Функция возрастает

π

π

π

3π

, k ϵ Z

, k ϵ Z

при х ϵ [- - +2πk ; - + 2πk ]

при х ϵ [ - +2πk; - +2πk]

2

2

2

2

y

1

p

- p

5p

- 3p

3p

- 5p

-2π

-π

2π

π

2

2

IIIIIIIIIIIIIIIIIIIIIIII

IIIIIIIIIIIIIIIIIIIIIII

IIIIIIIIIIIIIIIIIIIIIIII

IIIIIIIIIIIIIIIIIIIIIIII

IIIIIIIIIIIIIIIIIIIIIIII

0

2

2

2

2

x

-1

Функция принимает отрицательные значения

Функция принимает положительные значения

на интервалах (0+2πk; π+2πk),

т.е., на интервалах (2πk; π+2πk), k ϵ Z.

на интервалах (π+2πk; 2π+2πk), k ϵ Z.

y

1

p

- p

5p

- 3p

3p

- 5p

-2π

-π

2π

π

2

2

0

2

2

2

2

x

-1