Презентация к уроку "Гармонические колебания". 11 класс

Повторение пройденного.

• Какое движение называется колебательным?

• Что является главным отличием колебательного движения от других видов движения?

Какой общей чертой ( кроме периодичности) обладают движения тел, изображенных на слайде?

Повторение пройденного.

• Какие виды колебаний вы знаете?

• Какие колебания называются свободными ?

• Какие системы тел называются колебательными?

Математический маятник.

Пружинный маятник

Происхождение слова гармония гармо́ния Латинское — harmonia.

Оно пришло из латинского через польский и восходит к греческому со значением «связь», «согласованность», «совместимость». Изначально слово «гармония» употреблялось как музыкальный термин и имело значение «строй», «лад», «порядок» и уже позже стало использоваться в переносном абстрактном значении.

Гармонические колебания

Гармонические колебания

Свободные колебания, которые происходят под действием силы, пропорциональной смещению и направленной противоположно ему, называют гармоническими колебаниями.

Косинусоида

Косинусоида

Косинусоида

Гармонические колебания – периодические изменения во времени координаты тела, происходящие по закону синуса или косинуса.

Параметры, описывающие

колебательное движение

Давайте вспомним

Амплитуда- …

максимальное отклонение тела от положения равновесия.

Х max =0,2 см

Давайте вспомним

Период- …

время, за которое тело совершает одно полное колебание.

Т = 4·10 -3 с

Давайте вспомним

Частота- …

число полных колебаний, совершенных за единицу времени.

1

ν =

Т

1

ν = = 250 Гц

4 · 10 -3 с

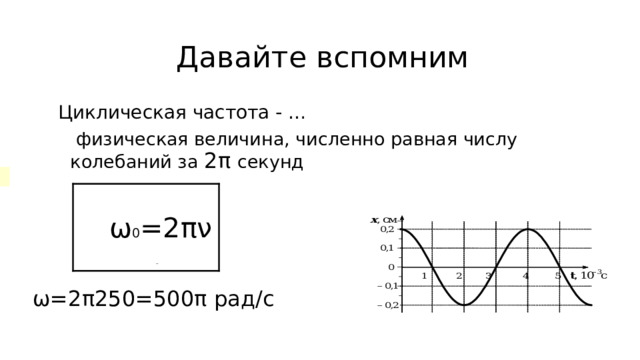
Давайте вспомним

Циклическая частота - …

физическая величина, численно равная числу колебаний за 2 π секунд

1

ω 0 =2 πν

Т

ω =2 π 250=500 π рад/с

ОСНОВНЫЕ ХАРАКТЕРИСТИКИ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ

x – смещение точки от положения равновесия в данный момент времени ( мгновенное значение).

X m – модуль максимального смещения точки от положения равновесия называется амплитудой ;

φ = ω 0 t

φ = ω 0 t + φ 0 – фаза колебаний , которая определяет состояние колебательной системы в любой момент времени; φ = [ рад ]

24

Периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса, называются ГАРМОНИЧЕСКИМИ КОЛЕБАНИЯМИ

x

x m

φ

3 π /2

2 π

π

π /2

t

0

T

T/2

T/4

3T/4

x m

x = X m sin ω 0 t

уравнение гармонического колебания

x = X m cos ω 0 t

26

Периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса, называются ГАРМОНИЧЕСКИМИ КОЛЕБАНИЯМИ

x

x m

φ

2 π

3 π /2

π

π /2

t

0

T

T/2

T/4

3T/4

x m

x = X m sin( ω t + φ 0 )

уравнение гармонического колебания

x = X m cos( ω t + φ 0 )

27

Период и частота колебания пружинного маятника :

0

Период и частота колебаний математического маятника

0