Презентация к уроку геометрии в 10 классе "Параллельные прямые в пространстве. Параллельность трёх прямых"

10 класс ГЕОМЕТРИЯ

Параллельные прямые в пространстве. Параллельность трёх прямых

Автор презентации: Попов Дмитрий Сергеевич

На данном уроке мы введём понятия параллельных прямых в пространстве, сформулируем лемму о пересечении плоскости двумя параллельными прямыми, докажем теорему о параллельности трёх прямых, а также закрепим эти понятия на примерах.

Геометрия, которую мы изучаем, называется евклидовой, по имени древнегреческого ученого Евклида (3 век до нашей эры), который создал целый труд по математике под названием «Начала». В данной книге есть раздел о параллельных прямых.

Евклид

В советском энциклопедическом словаре слово «параллельность» переводится с греческого языка, как «идущий рядом».

В средние века параллельность обозначалась знаком «=». В 1557 году Р. Рекордом для обозначения равенства был введен знак «=», которым мы пользуемся сейчас, а параллельность стали обозначать «║».

В книге «Начала» определение параллельных прямых звучало так « прямые, лежащие в одной плоскости и будучи бесконечно продолжены в обе стороны, ни с той, ни с другой стороны не пересекаются ». Это определение почти не отличается от современного.

ВСПОМНИМ ПОНЯТИЕ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ В ПЛАНИМЕТРИИ

Параллельные прямые  – две прямые на плоскости называются параллельными, если они не пересекаются.

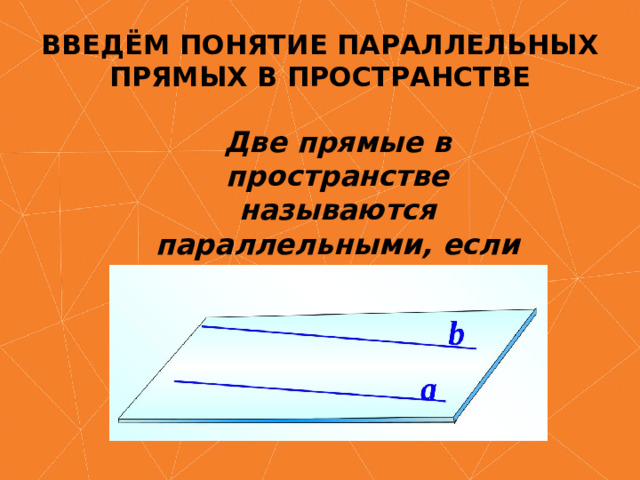
ВВЕДЁМ ПОНЯТИЕ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ В ПРОСТРАНСТВЕ

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не совпадают .

ТЕОРЕМА О ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ

ТЕОРЕМА 1. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и при том только одна.

ЛЕММА

ТЕОРЕМА 1. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

ТЕОРЕМА О ТРЁХ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ

ТЕОРЕМА 2. Если две прямые параллельны третьей прямой, то они параллельны.

Попробуйте самостоятельно доказать данную теорему, если не получается, то воспользуйтесь учебником (стр. 11)

РАССМОТРИМ РЕШЕНИЕ ЗАДАЧИ №17

Задача 17.  M, N, Q и P — середины отрезков DB, DC, AC и AB. Найдите периметр четырехугольника MNQP, если AD = 12 см, BC = 14 см.

Решение: 1) MN║ ВС, как средняя линия в треугольнике BDC, PQ║ ВС, как средняя линия в треугольнике АСВ. По теореме о трёх параллельных прямых: MN║ ВС, PQ║ ВС ⇒ MN║PQ.

2) Аналогично можно доказать, что

РМ║DА, NQ║DA ⇒ PM║NQ.

3) Исходя из вышеперечисленного, MNQP – параллелограмм.

4) ВС = 2PQ ⇒ PQ = 7. 5) AD = 2PM ⇒ PM = 6. 6) P MNQP = 2(6 + 7) = 26 см.

Ответ: 26 см.

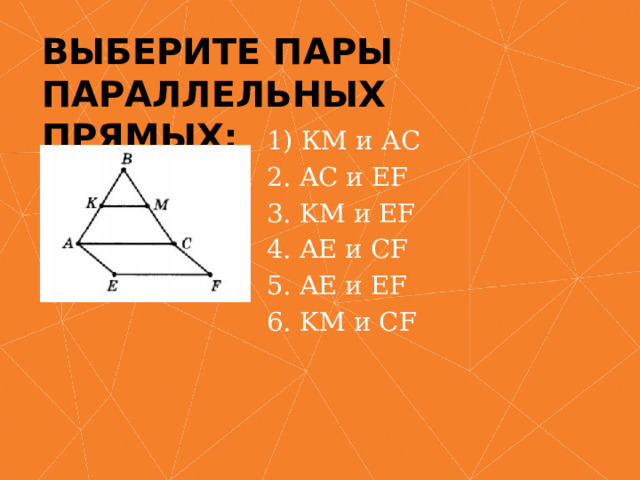
Выберите пары параллельных прямых:

1) КМ и АС

2. AC и EF

3. KM и EF

4. AE и CF

5. AE и EF

6. KM и CF

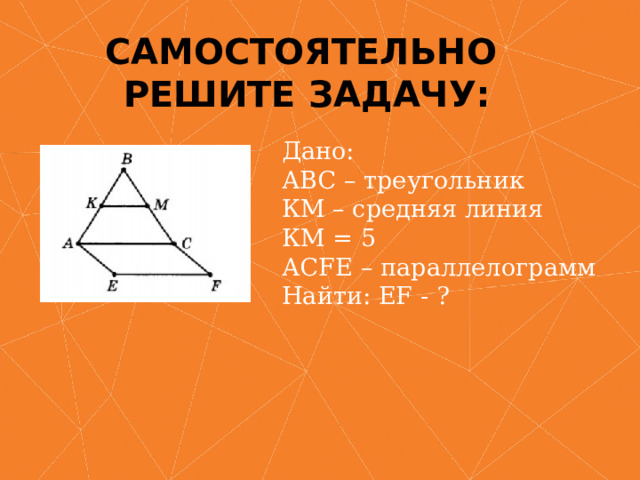
Самостоятельно Решите задачу:

Дано: АВС – треугольник КМ – средняя линия КМ = 5 АСFE – параллелограмм Найти: EF - ?

ДОМАШНЕЕ ЗАДАНИЕ:

1) Изучите п. 4, 5 2) Выучить определение параллельных прямых на плоскости, теоремы и лемму. 2) Решите №№20, 29.

Использованные ресурсы:

• https://resh.edu.ru/subject/lesson/6065/start/125651 /
• https:// youtu.be/LYMHppeymYs
• https:// file.11klasov.net/19-geometriya-uchebnik-dlya-10-11klassov-atanasyan-ls-i-dr.html