Презентация к уроку геометрии в 9 классе "Площадь круга и его элементов (сектора и сегмента)"

9 класс ГЕОМЕТРИЯ 9 марта

Площадь круга и его элементов (сектора и сегмента).

Автор презентации: Попов Дмитрий Сергеевич

Ваша задача на сегодня:

• Ознакомиться с материалом слайдов 3 – 10.
• Ознакомься с рекомендациями по выполнению заданий на слайде 11 и выполни задания со слайдов 12 – 18.

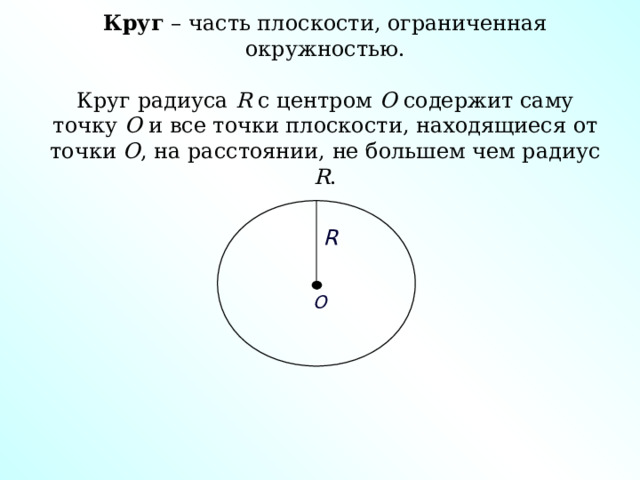
Круг – часть плоскости, ограниченная окружностью. Круг радиуса R с центром О содержит саму точку О и все точки плоскости, находящиеся от точки О , на расстоянии, не большем чем радиус R .

R

O

Рассмотрим вписанный в окружность правильный многоугольник.

Площадь данного круга будет больше площади многоугольника, так как он полностью находится в этом круге.

Учтем также, что площадь круга, вписанного в данный многоугольник, будет меньше площади самого многоугольника, так как круг полностью находится в самом многоугольнике.

Следовательно, справедливо следующее неравенство: S' n S n S (1)

Радиус вписанной в многоугольник окружности рассчитывается по формуле:

Предположим, что число сторон многоугольника неограниченно растёт , тогда справедливо будет выражение: .

Таким образом, можно сделать вывод, что радиус вписанной окружности стремится к радиусу описанной окружности .

Вывод. При неограниченном увеличении числа сторон правильного многоугольника вписанная в него окружность стремится к описанной окружности.

Поэтому и площадь вписанного круга будет стремиться к площади описанного круга: при .

Для вычисления площади круга радиусом R применим формулу площади правильного n -угольника: , где P n – периметр n -угольника A 1 A 2 A n .

Принимая во внимание, что радиус вписанной окружности стремится к радиусу описанной окружности, периметр n -угольника также стремится к длине окружности, , а площадь вписанной окружности стремится к площади описанной окружности при запишем формулу для вычисления площади круга с радиусом R:

– площадь круга радиусом R.

Круговой сектор

Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы с центром круга.

Дуга, ограничивающая сектор, называется дугой сектора .

Круговой сектор

Выведем формулу для вычисления площади закрашенного сектора круга радиуса R и ограниченного дугой с градусной мерой .

Площадь всего круга: .

Площадь кругового сектора, ограниченного дугой в 1° равна .

Площадь S кругового сектора с произвольным углом α будет равна:

Круговой сегмент

Круговым сегментом или просто сегментом называется часть круга, ограниченная дугой окружности и хордой, соединяющей концы этой дуги.

При значении градуса дуги менее, чем 180°, площадь сегмента можно вычислить путем вычитания из площади сектора круга площадь равнобедренного треугольника, сторонами которого являются два радиуса и хорда сегмента.

α

РЕКОМЕНДАЦИИ К ВЫПОЛНЕНИЮ ЗАДАНИЙ:

Задание 1. Перепиши в тетрадь предложение, вставив в него пропущенное слово.

Задание 2. Запиши краткое решение задачи.

Задание 3. Запиши краткое решение задачи.

Задание 4. Запиши краткое решение задачи.

Задание 5. Запиши только ответ.

Также выполните задания со слайда 17.

Задание 1. Впишите пропущенное слово:

Кругом называется часть  __________, ограниченная окружностью.

Задание 2. Питон длиной 7 м свернулся в круг. Найдите площадь образуемого им круга.

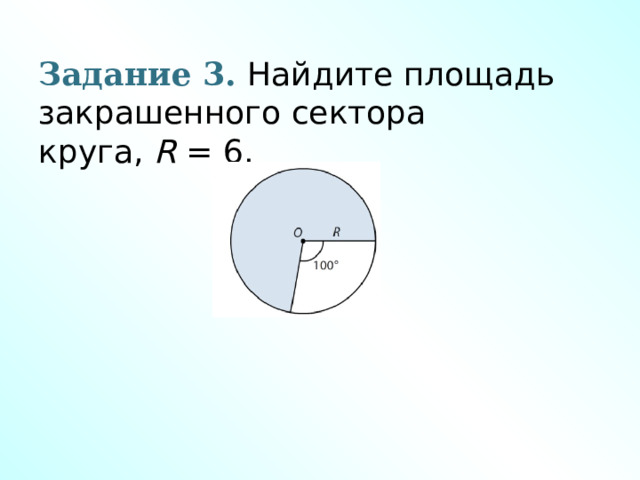
Задание 3. Найдите площадь закрашенного сектора круга,  R  = 6.

Задание 4. Рассчитайте площадь закрашенного сектора, если  r  = 8,  R  = 13, Α = 125°. Ответ округлите до десятых.

Задание 5. Радиус круга увеличили в 2 раза. Во сколько раз увеличилась его площадь?

По учебнику выполните №1127, №1128.

Рекомендации к выполнению: при решении задания вы должны сделать рисунок, написать дано, решение и ответ.

Выполненные работы отправить на электронную почту учителя до 14.03.2023

Удачи в усвоении новых знаний и решении заданий!

Спасибо за внимание!