Презентация к уроку математики в 11 классе "Первообразная и интеграл"

Первообразная и интеграл

Немного истории

Интегральное исчисление появилось во времена античного периода развития математической науки и началось с метода исчерпывания, который представлял собой набор правил для вычисления площади и объема.

Евдокс Книдский

ок. 408 — ок. 355 год до н. э.

Метод получил своё развитие в работах Евклида.

Особым искусством и разнообразием применения метода исчерпывания прославился Архимед.

Королевский математик и астролог австрийского двора Иоганн Кеплер вывел формулы для вычисления объемов тел по нескольким измерениям.

Иоганн Кеплер

(1571 – 1630 )

Слово интеграл придумал Якоб Бернулли.

Символ ∫ введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова summa).

Я́коб Берну́лли

(1654 – 1705)

Ньютон и Лейбниц открыли независимо друг от друга факт, известный под названием формулы

Ньютона – Лейбница .

Готфрид Вильгельм фон Лейбниц (1646—1716)

Исаак Ньютон

(1643 – 1727)

Работы Коши и Вейерштрасса

подвели итог многовековому развитию интегрального исчисления.

Карл Теодор Вильгельм Вейерштрасс

(1815 1897 )

Огюстен Луи Коши

(1789 – 1857)

В развитии интегрального исчисления приняли участие русские математики:

М.В. Остроградский

(1801 – 1862)

П.Л. Чебышев

(1821 – 1894)

В.Я. Буняковский

(1804 – 1889)

Интеграл принадлежит к числу математических понятий, происхождение и развитие которых тесно связано с решением прикладных задач.

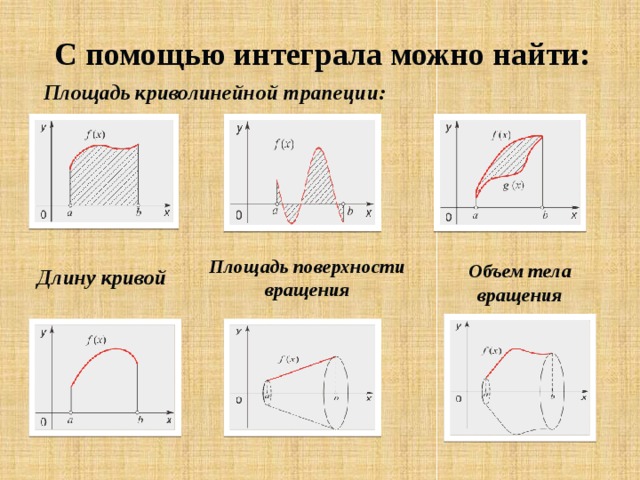
С помощью интеграла можно найти:

Площадь криволинейной трапеции:

Площадь поверхности вращения

Объем тела вращения

Длину кривой

С помощью интеграла можно вычислить:

путь, пройденный точкой

работу переменной силы

силу давления жидкости и газа

координаты центра тяжести

массу стержня

Первообразная и неопределенный интеграл

Таблица первообразных

Основные свойства неопределенного интеграла:

• Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная:

• Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции:

• Неопределенный интеграл алгебраической суммы функций равен алгебраической сумме неопределенных интегралов этих функций:

Основные свойства неопределенного интеграла:

• Постоянный множитель подынтегрального выражения можно выносить за знак неопределенного интеграла:

и

• Если

– любая известная функция, имеющая непрерывную производную, то

Основные формулы интегрирования (таблица интегралов):

(n

);

Примеры

Домашнее задание

• П. 6.1,
• № 6.13(е). 6.15(б)
• Подготовить сообщения о математиках, внесших вклад в изучение интегрального исчисления