Презентация к уроку по геометрии на тему: "Окружность, вписанная в треугольник"

Тема урока: свойство высот треугольника

Презентация выполнена учителем математики МОАУ «СОШ № 27 г.Орска»

Левшиной О.А.

Цели и задачи урока

• Предметные   - рассмотреть теорему о точке пересечения высот треугольника
• Личностные   - формировать интерес к изучению темы и желание применять приобретённые знания и умения.
• Метапредметные  – совершенствовать навыки решения задач по готовым чертежам.
• Задачи: 1) доказать теорему о точке пересечения высот треугольника.
• 2) развивать навык решения задач.
• 3) рассмотреть по чертежам ортоцентры.

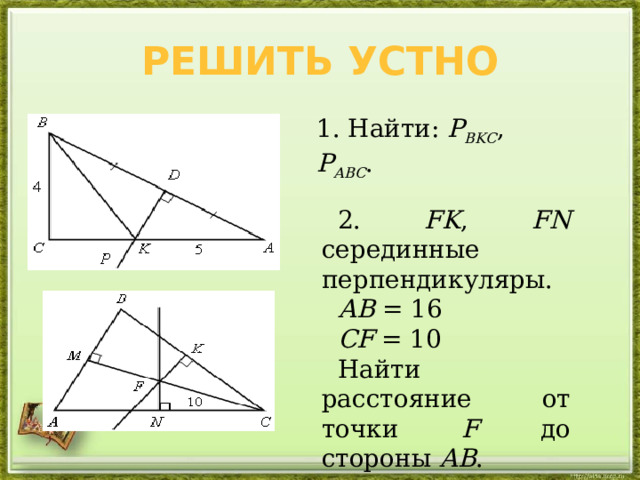
Решить устно

1. Найти: Р ВKС , Р АВС .

2. FK , FN серединные перпендикуляры.

АВ = 16

СF = 10

Найти расстояние от точки F до стороны АВ .

Теоретический опрос

• * Что вам известно о точках биссектрисы неразвёрнутого угла?
• * Сформулируйте теорему обратную данной.
• * Сформулируйте свойство биссектрис треугольника.
• * Дайте определение серединного перпендикуляра к отрезку.
• * Каким свойством обладает каждая точка серединного перпендикуляра к отрезку?
• * Сформулируйте теорему обратную данной.
• * Сколько серединных перпендикуляров можно построить в треугольнике? Каким свойством они обладают?

• « Геометрия является самым могущественным средством для изощрения наших умственных способностей и даёт нам возможность правильно мыслить и рассуждать» Г.Галилей
• – Сегодня мы продолжим изучение темы «Замечательные точки треугольника» и познакомимся с теоремой о точке пересечения высот в треугольнике.

. Теорема. Высоты треугольника (или их продолжения) пересекаются в одной точке .

• Доказательство:
• 1. Проведём: С 2 B 2 ║BC, A 2 C 2 ║AC, A 2 B 2 ║AB так, что B Є A 2 C 2 , C Є A 2 B 2 ,
• A Є B 2 C 2 . Получим Δ A 2 B 2 C 2 .
• 2. AB= A 2 C, AB= С 2 B 2 точки A, B и C– середины сторон Δ A 2 B 2 C 2 , т.е. прямые АА 1 , BB 1 , CC 1 -серединные перпендикуляры к сторонам Δ A 2 B 2 C 2 
• O= AA 1  BB 1  CC 1 .

ортоцентр

• Три высоты треугольника всегда пересекаются в одной точке, называемой ортоцентром треугольника. Ортоцентр остроугольного треугольника (точка O на рис. ниже) расположен внутри треугольника, а ортоцентр тупоугольного треугольника – снаружи; ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.

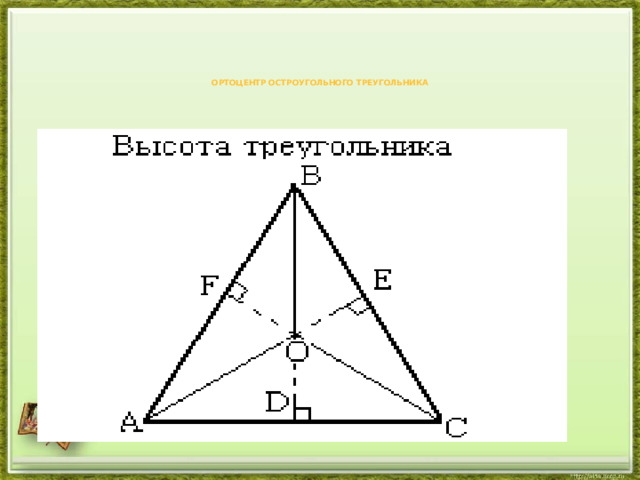
Ортоцентр остроугольного треугольника

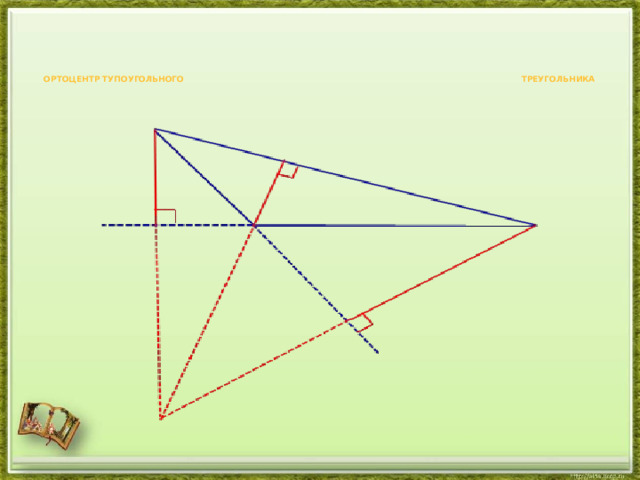
ортоцентр тупоугольного треугольника

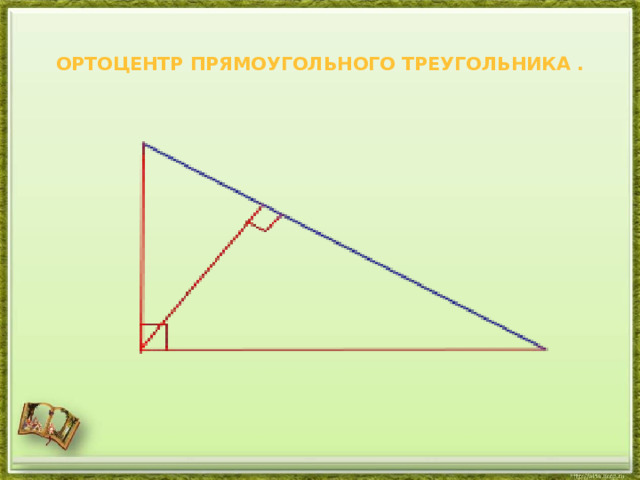
Ортоцентр прямоугольного треугольника .

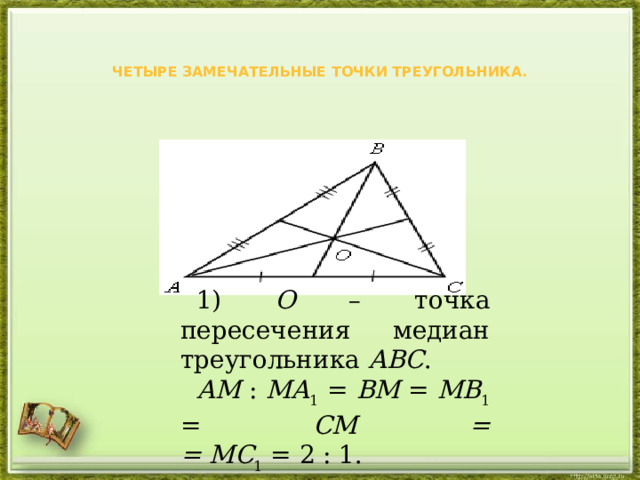
Четыре замечательные точки треугольника.

1) О – точка пересечения медиан треугольника АВС .

АМ : МА 1 = ВМ = МВ 1 = СМ = = МС 1 = 2 : 1.

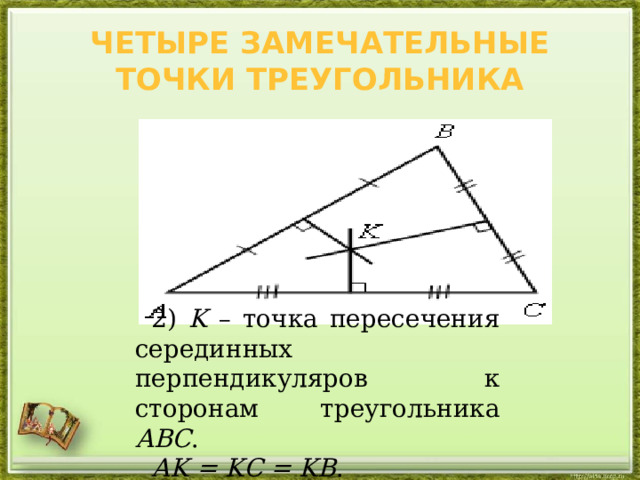
Четыре замечательные точки треугольника

2) K – точка пересечения серединных перпендикуляров к сторонам треугольника АВС .

АK = KС = KВ .

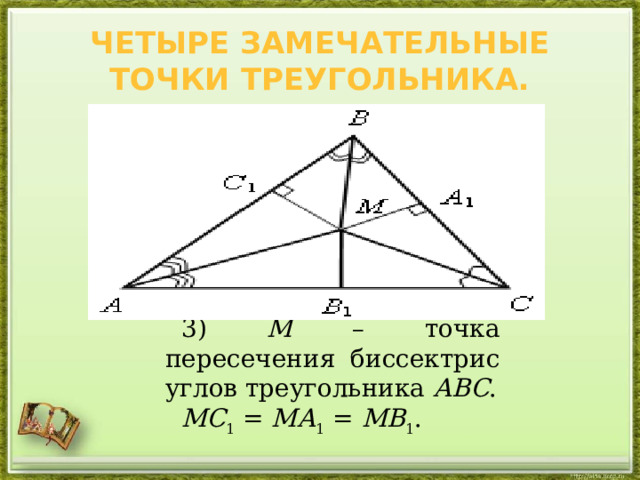
Четыре замечательные точки треугольника.

3) М – точка пересечения биссектрис углов треугольника АВС .

МС 1 = МА 1 = МВ 1 .

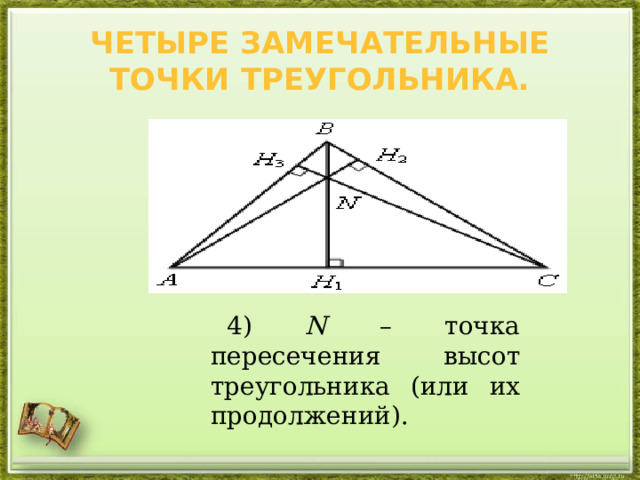
Четыре замечательные точки треугольника.

4) N – точка пересечения высот треугольника (или их продолжений).

Домашнее задание: вопросы 1– 20, с. 187–188; №№ 688, 720.