© 2021, Нугаева Хамис Магомедовна 949 10
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 21.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 25.02.2021 11:08
Нугаева Хамис Магомедовна
учитель математики
56 лет
673
79 346 
Презентация к уроку по математики на тему: "Теоремы Чевы и Менелая"
Категория:
Математика
21.02.2021 20:30
Просмотр содержимого документа
«Презентация к уроку по математики на тему: "Теоремы Чевы и Менелая"»
Геометрия 10 класс (профильный уровень)
Изучение нового материала
Теорема Менелая
Менелай Александрийский – древнегреческий математик ( I в.н.э.)
Пусть на сторонах или продолжениях сторон АВ, ВС и СА треугольника АВС отмечены точки С 1 , А 1 , В 1 , не совпадающие с его вершинами, причем .
Тогда если точки С 1 , А 1 , В 1 лежат на одной прямой, то р qr=-1 ; обратно: если р qr=-1 , то точки С 1 , А 1 , В 1 лежат на одной прямой.
В
С1
А 1
А
С
В 1
Пусть точка А 1 лежит на стороне ВС треугольника АВС, точка С 1 – на стороне АВ, точка В 1 – на продолжении стороны АС за точку С. Тогда точки А 1 , В 1 и С 1 лежат на одной прямой тогда и только тогда, когда выполняется равенство
Изучение нового материала
В
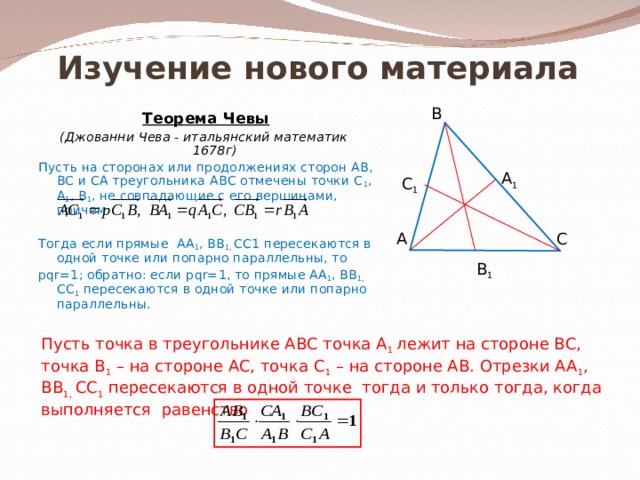
Теорема Чевы
(Джованни Чева - итальянский математик 1678г)
Пусть на сторонах или продолжениях сторон АВ, ВС и СА треугольника АВС отмечены точки С 1 , А 1 , В 1 , не совпадающие с его вершинами, причем
Тогда если прямые АА 1 , ВВ 1, СС1 пересекаются в одной точке или попарно параллельны, то
р qr=1 ; обратно: если р qr=1 , то прямые АА 1 , ВВ 1, СС 1 пересекаются в одной точке или попарно параллельны.
А 1
С 1
А
С
В 1
Пусть точка в треугольнике АВС точка А 1 лежит на стороне ВС, точка В 1 – на стороне АС, точка С 1 – на стороне АВ. Отрезки АА 1 , ВВ 1, СС 1 пересекаются в одной точке тогда и только тогда, когда выполняется равенство
Решение задач
№ 1. В треугольнике АВС на стороне ВС взята точка N так, что NC=3BN ; на продолжении стороны АС за точку А взята точка М так, что МА=АС. Прямая MN пересекает сторону АВ в точке F . Найдите отношение .
Решение задач
№ 2 . В треугольнике АВС, описанном около окружности, АВ = 8, ВС = 5, АС = 4. А 1 и С 1 – точки касания, принадлежащие соответственно сторонам ВС и ВА. Р – точка пересечения отрезков АА 1 и СС 1 . Точка Р лежит на биссектрисе ВВ 1 . Найдите АР : РА 1 .
Решение:
- Точка касания окружности со стороной АС не совпадает с В 1 , так как треугольник АВС – разносторонний.
- Пусть С 1 В = х, тогда, используя свойство касательных, проведенных к окружности из одной точки, введем обозначения 8 – х + 5 – х = 4, х =4,5.
- Значит, С 1 В = ВА 1 = 4,5, А 1 С = 5 – 4,5= 0,5 АС 1 = 8 – 4,5=3,5 .
- В треугольнике АВА 1 прямая С 1 С пересекает две его стороны и продолжение третьей стороны. По теореме Менелая …
Ответ: 70 : 9.
Решение задач
№ 2. В треугольнике АВС, описанном около окружности, АВ=13, ВС=12, АС=9,
А 1 и С 1 – точки касания, лежащие соответственно на сторонах ВС и АВ.
N – точка пересечения отрезков АА 1 и ВВ 1 . Точка N лежит на высоте ВВ 1 . Найдите отношение BN:NB 1 .
.
Домашнее задание
пп.95,96
Задачи.
- В треугольнике АВС А D – медиана, точка О– середина медианы. Прямая ВО пересекает сторону АС в точке К. В каком отношении точка К делит АС, считая от точки А? ( Примечание. Рассмотрите треугольник А DC )
- Стороны треугольника 5, 6 и 7. Найдите отношение отрезков, на которые биссектриса большего угла треугольника разделена центром окружности, вписанной в треугольник.
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
