Презентация к уроку-тренингу

«Легко в учении – тяжело в походе, тяжело в учении – легко в походе.

Тяжело в учении – легко в бою» А.В. Суворов.

Урок-тренинг по геометрии в 9 классе

« Решение планиметрических задач по темам «Теорема Пифагора» и «Подобие треугольников» из открытого банка заданий ОГЭ »

Математический диктант

1.Закончите предложение:

Два треугольника  называются подобными, если их углы соответственно равны и стороны одного треугольника … пропорциональны сторонам другого

2. Закончите предложение:  Отношение периметров двух подобных треугольников равно… коэффициенту подобия.

3. Подобны ли треугольники, если два угла одного треугольника равны двум углам другого ? Да

4. Подобны ли два равносторонних треугольника? Да

5. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов? Да

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

c

a

b

Сайт «Распечатай и реши»

Лучшее время -   время для математики Решайте вместе с нами!

2,4 м

13 м

2,4 м

х

15 м

4 м

ОТВЕТ 12 м

13 см

х

12 см

ОТВЕТ 5 см

15 ступенек

96 см

28 см

ОТВЕТ 15 м

Пусть у двух треугольников АВС и А 1 В 1 С 1 углы соответственно равны

В

В 1

А

С

С 1

А 1

В этом случае стороны АВ и А 1 В 1 , ВС и В 1 С 1 , СА и С 1 А 1 называются сходственными.

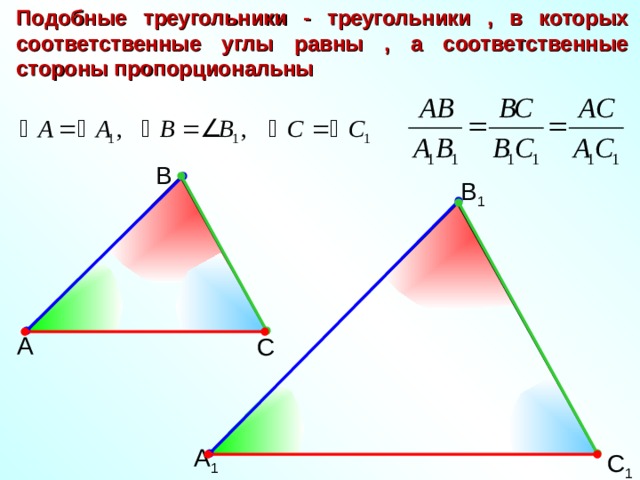
Подобные треугольники - треугольники , в которых соответственные углы равны , а соответственные стороны пропорциональны

В

В 1

А

С

А 1

С 1

Число k , - это коэффициент подобия, равный отношению сходственных сторон подобных треугольников

= k

A 1 B 1 C 1

ABC

В 1

В

А

С

С 1

А 1

13

Блиц-опрос

ABC

Найдите: х, у, z.

А 1 В 1 С 1

Дано:

В

В 1

С.М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах»

у

10,5 см

9 см

х

18 см

21 см

А

С

z

12 см

С 1

24 см

А 1

14

Блиц-опрос

Найдите: х, у .

А 1 В 1 С 1

ABC

Дано:

В

В 1

7 см

6 см

С.М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах»

х

21 см

18 см

А

С

8 см

С 1

у

А 1

24 см

15

Блиц-опрос

ABC

Найдите: х, у .

А 1 В 1 С 1

Дано:

В 1

В

6 см

х

12 см

у

7 см

С.М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах»

А

14 см

8 см

А 1

С

16 см

С 1

16

С 1

С

А

В

А 1

В 1

17

С 1

С

 АВС  А 1 В 1 С 1

А

В

А 1

В 1

18

С

С 1

 АВС  А 1 В 1 С 1

А

В

А 1

В 1

19

19

19

Х

1 м

ОТВЕТ 2,5 м

19

25 м

19

( х+ 8) м

19

320 см

100 см

230 см

Х

19

Рассказывают, что египетский фараон Амазис приказал измерить высоту пирамиды Хеопса. Жрецы не знали, как выполнить эту задачу. И тогда им на помощь пришел Фалес. Собравшиеся у подножия пирамиды жрецы с интересом следили за действиями милетского мудреца, который очертил вокруг себя окружность, радиус которой был равен его росту. Фалес стал в центре окружности и стал дожидаться, когда конец его тени достигнет окружности. Когда это произошло, Фалес быстро направился к месту на земле, где заканчивалась тень пирамиды, и положил там камень. Фалес справедливо считал, что в этот момент и тень от пирамиды равна высоте самой пирамиды. Затем Фалес измерил расстояние от камня до подножия пирамиды, прибавил к этому расстоянию половину длины основания пирамиды и огласил результат своего труда

19

Источники

• https://math-oge.sdamgia.ru/
• http://www.fipi.ru/content/otkrytyy-bank-zadaniy-oge
• https://www.time4math.ru/oge

19