Презентация к занятию "Декартовы координаты в пространстве"

Раздел 3. Координаты и векторы

Декартовы координаты в пространстве. Расстояние между двумя точками. Координаты середины отрезка

Рене Декарт

• Родился в 1596 г. в городе Лаэ на юге Франции, в дворянской семье. Отец хотел сделать из Рене офицера.

Ла-Рошаль

Для этого в 1613 г. он отправил Рене в Париж. Много лет пришлось Декарту пробыть в армии, участвовать в военных походах в Голландии, Германии, Венгрии, Чехии, Италии, в осаде крепости гугенотов Ла-Рошали

• Но Рене интересовала философия, физика и математика. Вскоре по приезде в Париж он познакомился с учеником Виета, видным математиком того времени — Мерсеном, а затем и с другими математиками Франции

Марен Мерсен

Будучи в армии, Декарт все свое свободное время отдавал занятиям математикой.

Он изучил алгебру немецких, математику французских и греческих ученых.

• После взятия Ла-Рошали в 1628 г. Декарт уходит из армии. Он ведет уединенный образ жизни с тем, чтобы реализовать намеченные обширные планы научных работ.

Философские взгляды Декарта не соответствовали требованиям католической церкви.

Поэтому он переселился в Голландию, где прожил 20 лет, с 1629 по 1649 г., но из-за гонений протестантской церкви в 1649 г. переехал в Стокгольм.

• Но суровый северный климат Швеции оказался для Декарта губительным, и он умер от простуды в 1650 г.

• Декарт был крупнейшим философом и математиком своего времени. В основе его философии лежал материализм.

• Самым известным трудом Декарта является его “Геометрия”. Декарт ввел систему координат, которой пользуются все и в настоящее время

• Он установил соответствие между числами и отрезками прямой и таким образом ввел алгебраический метод в геометрию.

• Эти открытия Декарта дали огромный толчок развитию как геометрии, так и другим разделам математики, оптики.

Это был совершенно новый метод, отличавшийся красотой, изяществом и простотой

• Декарт впервые ввел координатную систему, которая существенно отличалась от общепринятой в наши дни.
• Он использовал косоугольную систему координат на плоскости, рассматривая кривую относительно некоторой прямой с фиксированной системой отсчета.

• Положение точек кривой задавалось с помощью системы параллельных отрезков, наклонных или перпендикулярных к исходной прямой.

• Декарт не вводил второй координатной оси, не фиксировал направления отсчета от начала координат

• Только в 18 в. сформировалось современное понимание координатной системы, получившее имя Декарта

Пьер Ферма

• Метод координат, предложенный в XVII в. Р.Декартом и П.Ферма, является мощным аппаратом, позволяющем переводить геометрические понятия на алгебраический язык.

С помощью метода координат можно было бы изложить весь школьный курс геометрии без единого чертежа , используя только числа и алгебраические операции.

В основе этого метода лежит понятие “система координат”.

Система координат

• Система координат -это способ задания положения точек на плоскости или в пространстве.

• Главное свойство всех систем координат:

положение любой точки однозначно определяется ее координатами

• (5;1), (6;2), (6;3), (5;6), (4;7), (5;8), (6;8), (8;9), (9;9), (7;8), (9;8), (6;7), (7;6), (9;6), (11;5), (12;3), (12;2), (13;3), (12;1), (7;1), (8;2), (9;2), (8;3), (6;1), (5;1) и (5;7)

Нанесите точки

Зайчонок

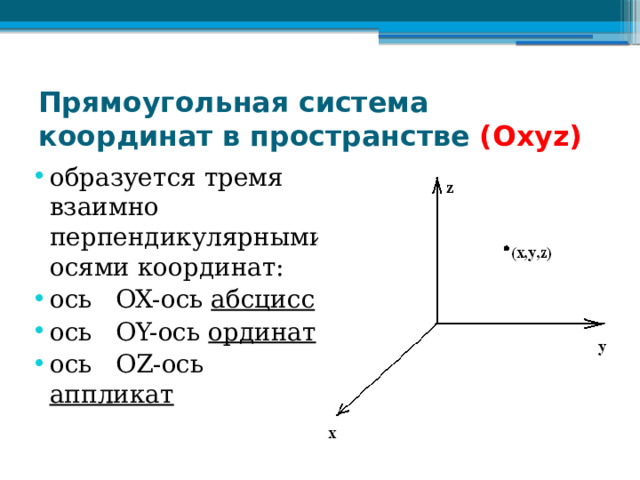
Прямоугольная система координат в пространстве (Оxyz)

• образуется тремя взаимно перпендикулярными осями координат:
• ось OX-ось абсцисс
• ось OY-ось ординат
• ось OZ-ось аппликат

• Координата х называется абсциссой точки ,
• координата   у — ординатой точки ,
• координата   z — аппликатой точки .

Отметьте точки А(4, 2,3) и В(6; -2; 4)

Координатные плоскости

• Три плоскости, проходящие через оси координат Ох и Оу, Оу и Оz, Оz и Ох, называются координатными плоскостями: Оху, Оуz, Оxz.

Координаты середины отрезка в пространстве

• Есть две произвольные точки A1(x1;y1;z1) и A2(x2;y2;z2). Тогда серединой отрезка A1A2 будет точка С с координатами x, y, z, где

Середина отрезка

Расстояние между двумя точками в пространстве

• Есть две произвольные точки A1(x1;y1;z1) и A2(x2;y2;z2) Тогда расстояние между точками A1 и A2 вычисляется по формуле

Длина отрезка

Задачи

• 1. Изобразите в прямоугольной системе координат отрезок АВ, найдите координаты его центра и его длину, если
• а) А(3; 2; 1), В (4; -1; 4)
• б) А(-1; 4; 3), В (5; -2; -3)
• в) А(5; -2; 4), В (-2; -2; -4)
• г) А(2; 5; 4), В (4; -2; -3)
• д) А(0; 2; 1), В (5; 0; 4)

РЕФЛЕКСИЯ

• Вы познакомились с понятием прямоугольной _________________________в пространстве.

• Узнали, что её задают три взаимно ________________прямые, на которых выбраны направления и единичные отрезки.

• Эти прямые называют __________________________
• Точку пересечения осей называют точкой __________________.

• Ось Ох называют осью ____________,

ось Оу называют осью ____________,

и новым для вас является название

оси Оz — ось _________________.

Помимо осей координат в прямоугольной системе координат присутствуют и координатные плоскости: ____________________.

• Всю прямоугольную систему координат в пространстве обозначают
• ______________________

• Любой точке пространства соответствует только одна тройка чисел __________, которые и являются её _____________.
• Все координаты точки О начала координат равны _____________.
• Координаты середины отрезка можно найти по формулам_________________________.
• Длину отрезка можно найти по формуле_____________________________.

СПАСИБО ЗА ВНИМАНИЕ!!!

Домашнее задание

• 1) Изобразите на плоскости

(1;-3), (2;-3), (3;-2), (3;3), (4;3), (5;4), (5;6), (4;7), (3;7), (2;6), (3;5), (3;5,5), (4;5), (3;4), (2;5), (-3;5),

(-4;6), (-4;9), (-5;10), (-5;11), (-6;10), (-7;10), (-7;10), (-7;8), (-9;8), (-9;7), (-8;6), (-6;6), (-7;3), (-6;2), (-6;-1), ў(-7;-2), (-7;-3), (-6;-3), (-4;-2), (-4;2), (1;2), (2;-1), (1;-2), (1;-3)

• 2)

Запишите координаты точек, по которым можно построить замок

• Изобразите в пространстве Д (1; 1 ;1), Е(2; -2; -3)
• Найдите длину отрезка ДЕ и координаты его середины