Презентация "Механические колебания"

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

9 класс

• Колебания - один из самых распространенных процессов в природе и технике
• Механические колебания – это движения, которые точно или приблизительно повторяются через равные промежутки времени.

Колебания

Свободные вынужденные автоколебания

• СВОБОДНЫЕ – колебания, возникающие в системе под действием внутренних сил
• ВЫНУЖДЕННЫЕ – колебания, совершаемые телами под действием внешних периодически меняющихся сил
• АВТОКОЛЕБАНИЯ – незатухающие колебания, которые могут существовать в системе без воздействия на нее внешних периодических сил, за счет источника энергии (например, часы с маятником)

УСЛОВИЯ ВОЗНИКНОВЕНИЯ СВОБОДНЫХ КОЛЕБАНИЙ

• при выведении тела из положения равновесия в системе должна возникнуть сила, стремящаяся вернуть его в положение равновесия;

• силы трения в системе должны быть достаточно малы.

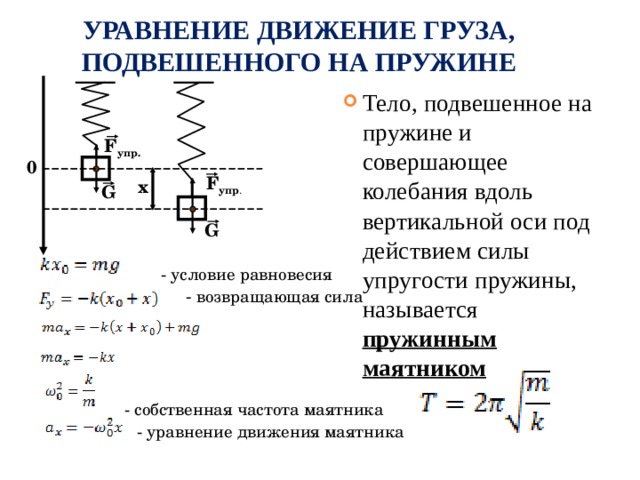
УРАВНЕНИЕ ДВИЖЕНИЕ ГРУЗА, ПОДВЕШЕННОГО НА ПРУЖИНЕ

• Тело, подвешенное на пружине и совершающее колебания вдоль вертикальной оси под действием силы упругости пружины, называется пружинным маятником

F упр.

- условие равновесия

- возвращающая сила

- собственная частота маятника

- уравнение движения маятника

0

F упр .

x

G

G

УРАВНЕНИЕ ДВИЖЕНИЯ МАТЕМАТИЧЕСКОГО МАЯТНИКА

При малых углах

• Математический маятник - подвешенный на тонкой невесомой нити груз, размерами которого можно пренебречь по сравнению с размерами нити.

s – длина дуги, l - длина маятника

• Уравнение движения математического маятника

ОСНОВНЫЕ ХАРАКТЕРИСТИКИ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ

• x m – модуль максимального смещения точки от положения равновесия называется амплитудой ;

• Т – время одного полного колнбания называется периодом ;

Т = t/n , где n – число полных колебаний

• x – смещение точки от положения равновесия в данный момент времени.

• число колебаний в единицу времени называется частотой ;

ѵ = 1/Т – линейная частота колебаний

ѵ = n/t [ ѵ ] = 1/c = 1 Гц (Герц)

Ѡ 0 =2 π /Т – циклическая частота колебаний

[ ѡ 0 ] = рад/с

• φ – фаза колебаний , которая определяет состояние колебательной системы в любой момент времени;

φ = ѡ 0 t + φ 0 [ φ ] = рад

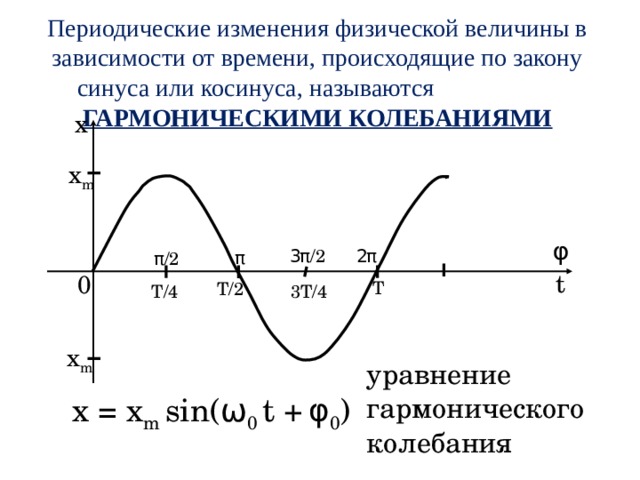
Периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса, называются ГАРМОНИЧЕСКИМИ КОЛЕБАНИЯМИ

x

x m

φ

3 π /2

2 π

π

π /2

t

0

T

T/2

T/4

3T/4

x m

уравнение гармонического колебания

x = x m sin( ω 0 t + φ 0 )

  x m ); b – красная кривая отличается от синей только значением периода ( T'  =  T  / 2); с – красная кривая отличается от синей только значением начальной фазы ( φ 0 ’ = - π /2  рад). " width="640"

Во всех трех случаях для синих кривых φ 0  = 0: а – красная кривая отличается от синей только большей амплитудой ( x' m    x m ); b – красная кривая отличается от синей только значением периода ( T'  =  T  / 2); с – красная кривая отличается от синей только значением начальной фазы

( φ 0 ’ = - π /2  рад).

Графики координаты x ( t ), скорости υ( t ) и ускорения a ( t ) тела, совершающего гармонические колебания.

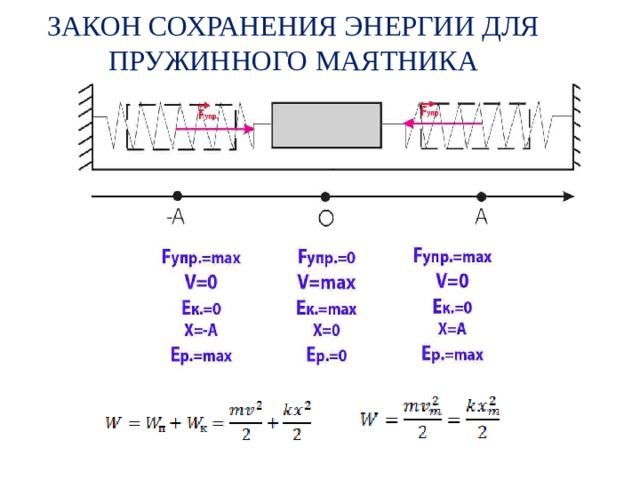
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ ДЛЯ ПРУЖИННОГО МАЯТНИКА

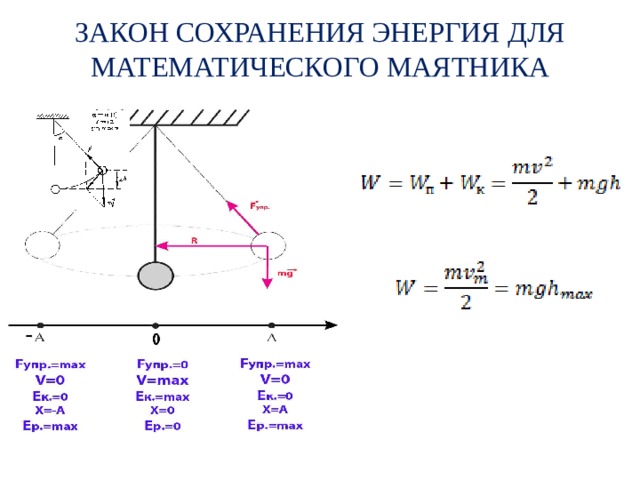
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИЯ ДЛЯ МАТЕМАТИЧЕСКОГО МАЯТНИКА

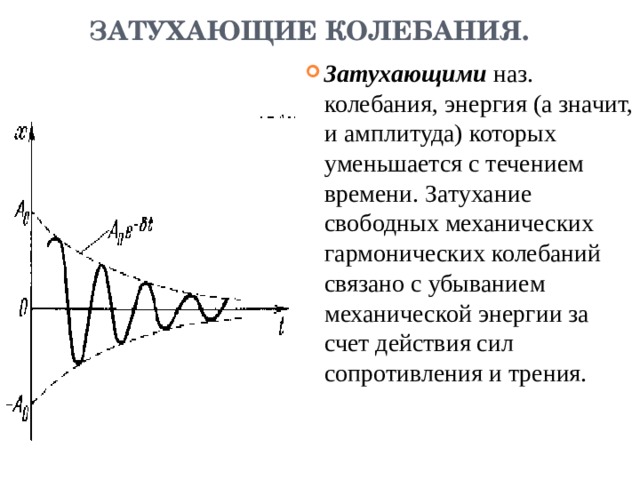
ЗАТУХАЮЩИЕ КОЛЕБАНИЯ.

• Затухающими наз. колебания, энергия (а значит, и амплитуда) которых уменьшается с течением времени. Затухание свободных механических гармонических колебаний связано с убыванием механической энергии за счет действия сил сопротивления и трения.

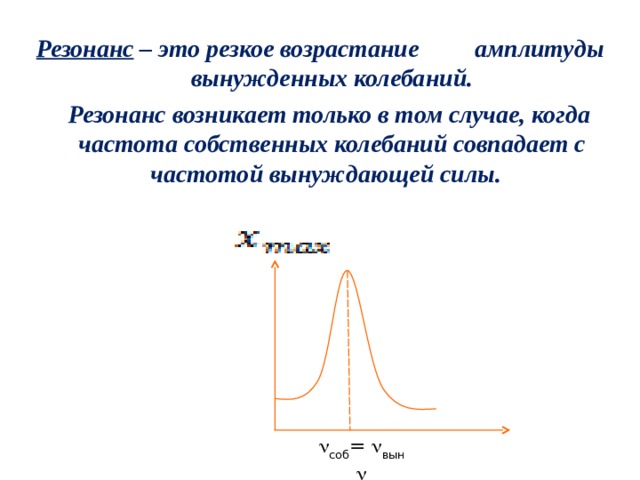
Резонанс – это резкое возрастание амплитуды вынужденных колебаний.

Резонанс возникает только в том случае, когда частота собственных колебаний совпадает с частотой вынуждающей силы.

 соб =  вын 