Презентация "Многогранники"

Учебно-исследовательская работа

«Многогранники»

Введение

При исследовании многогранников перед собой мы поставили следующие задачи:

• Изучить разновидности многогранников.

• Научиться строить некоторые модели многогранников.

• Исследовать вращающие кольца тетраэдров.

Многогранники

С древнейших времен наши представления о красоте связаны с симметрией. Наверное, этим объясняется интерес человека к многогранникам – удивительным символам симметрии, привлекавшим внимание выдающихся мыслителей.

Многогранник

Это пространственное тело с плоскими гранями и прямолинейными ребрами, устроенное так, чтобы всякое ребро соединяет две вершины и служит общей стороной двух граней

Простейшими примерами многогранников служат пирамиды и призмы

У пятиугольной призмы:

У пятиугольной пирамиды:

10 вершин

15 ребер

7 граней

6 вершин

10 ребер

6 граней

Антипризма (призмоид)

Основания одинаковые, но расположены различно: вершины каждого из оснований лежат над сторонами другого, так что боковые ребра идут зигзагом

У пятиугольной антипризмы:

10 вершин

20 ребер

12 граней

Теорема Эйлера

Для любого выпуклого многогранника справедливо соотношение

Г+В-Р=2

Г- число граней,

В- число вершин ,

Р- число ребер данного многогранника

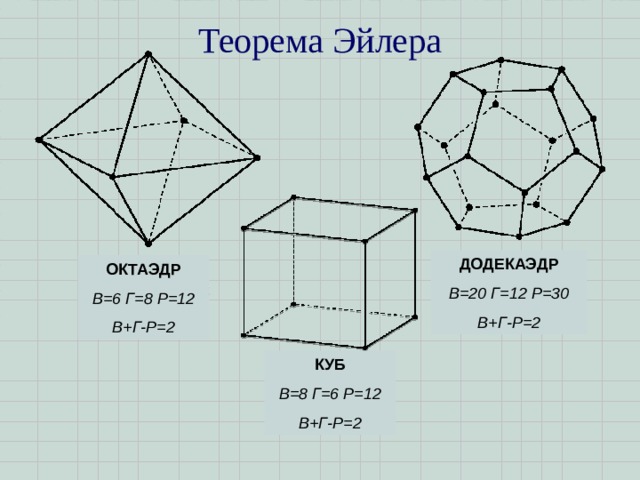
Теорема Эйлера

ДОДЕКАЭДР

В=20 Г=12 Р=30

В+Г-Р=2

ОКТАЭДР

В=6 Г=8 Р=12

В+Г-Р=2

КУБ

В=8 Г=6 Р=12

В+Г-Р=2

Правильные многогранники

Существует пять видов многогранников:

{ p , q }

V (в)

{3,3}

E (р)

4

{4,3}

8

F (г)

6

{3,4}

6

{5,3}

12

4

Название

6

20

12

{3,5}

Правильный тетраэдр

12

Куб

30

8

12

Октаэдр

30

Додекаэдр

20

Икосаэдр

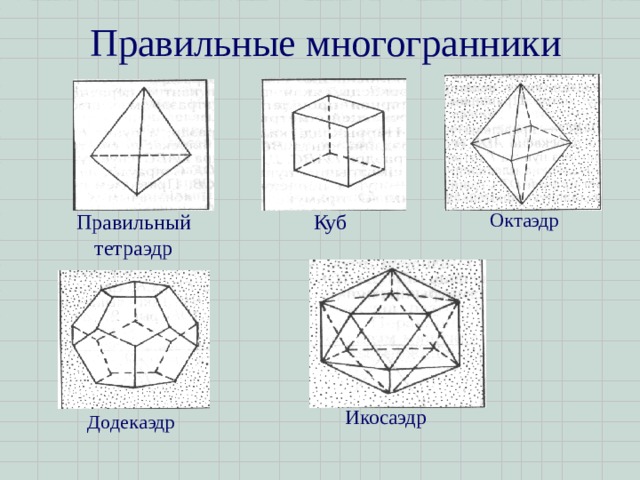
Правильные многогранники

Куб

Октаэдр

Правильный тетраэдр

Икосаэдр

Додекаэдр

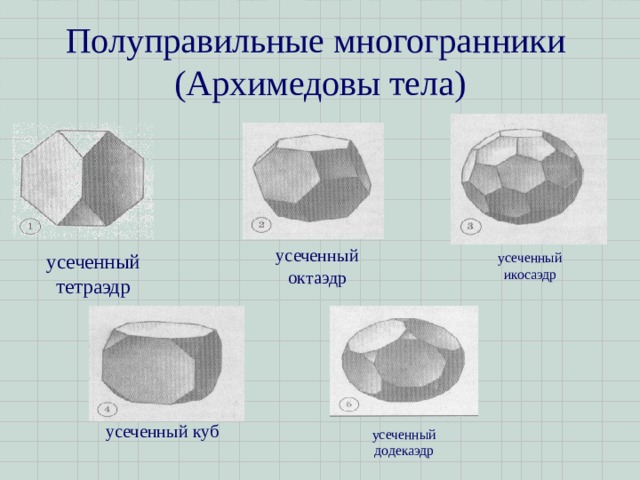
Полуправильные многогранники (Архимедовы тела)

усеченный октаэдр

усеченный тетраэдр

усеченный икосаэдр

усеченный куб

усеченный додекаэдр

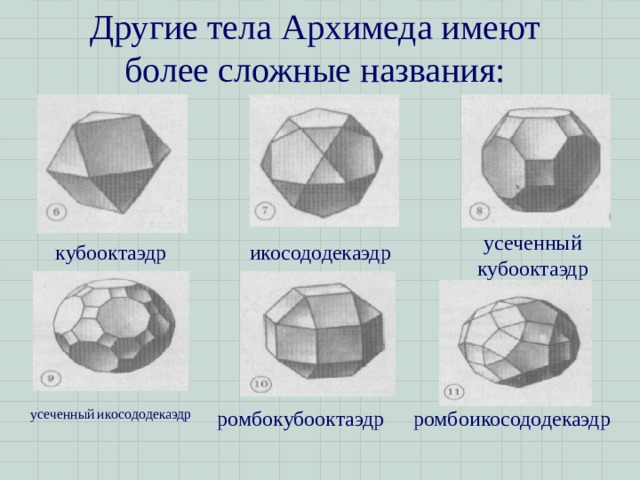
Другие тела Архимеда имеют более сложные названия:

усеченный кубооктаэдр

кубооктаэдр

икосододекаэдр

усеченный икосододекаэдр

ромбоикосододекаэдр

ромбокубооктаэдр

Вращающие кольца тетраэдров

Дж. М. Андреас и Р. М. Сталкер независимо друг от друга открыли семейство изгибаемых конечных многогранников с 2 n вершинами, 6 n ребрами и 4 n треугольными гранями. Гранями служат грани n тетраэдров, соединенных между собой в циклическом порядке по определенным парам противоположных ребер каждого, так что получается фигура наподобие кольца.

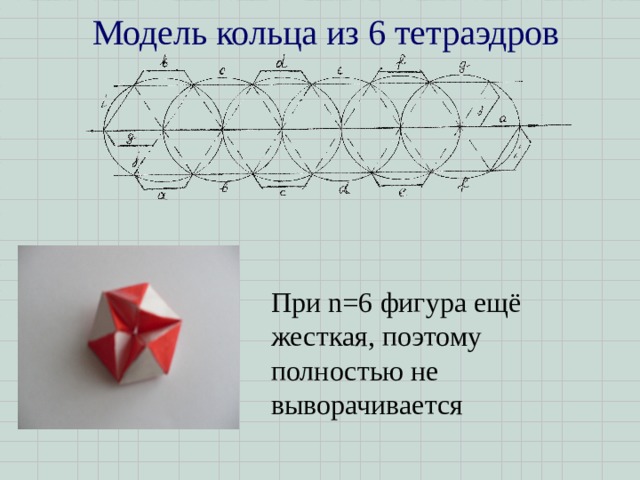
Модель кольца из 6 тетраэдров

При n=6 фигура ещё жесткая, поэтому полностью не выворачивается

Модель кольца из 8 тетраэдров

Заключение:

• Проводя исследования по данной теме, мы изучили исторические данные по многогранникам;
• При построении разверток многогранников мы научились работать с чертежными инструментами;
• Создавая модели призмы, антипризмы, пирамиды, а также вращающих колец из тетраэдров мы расширили свое пространственное воображение.

В дальнейшей работе мы хотим научиться строить модели более сложных по виду многогранников.