
Презентация к циклу уроков
по математике 9 класса
по теме: «Многогранники»

Тип урока:
урок ознакомления с новым материалом
Цели:
- формирование знаний о стереометрии и многогранниках;
- развитие умений сравнивать, выявлять закономерности, обобщать и умений соотносить математическую формулировку с графическим изображением.
2


Стереометрия – это раздел геометрии, в котором изучаются свойства фигур в пространстве
Слово «Стереометрия» происходит от греч. слов «стереос» - объемный и «метри-ос» - измерять.

Геометрические тела, как и другие геометрические фигуры являются воображаемыми объектами
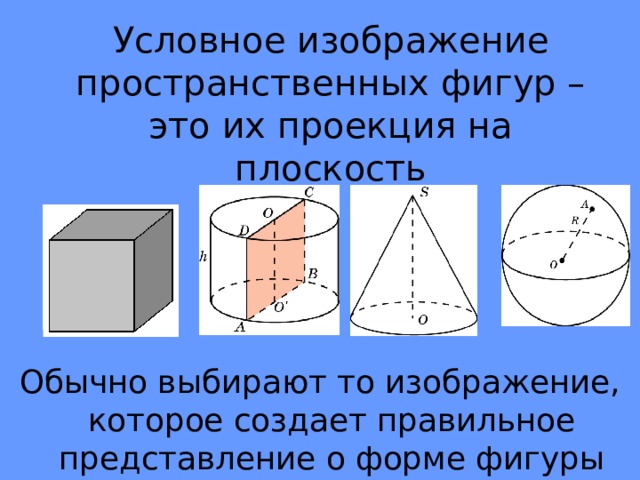
Условное изображение пространственных фигур – это их проекция на плоскость
Обычно выбирают то изображение, которое создает правильное представление о форме фигуры

Понятие многогранника является одним из централь-ных в курсе стереометрии .
Архимед
Многогранники как создания
в природе красивы и симметричны .

Чем же привлекательны многогранники?
Они обладают богатой историей, которая связана с такими знаменитыми учеными древности, как Пифагор, Евклид, Архимед.
В тоже время теория многогранников – современный раздел математики, имеющий практическое приложение в алгебре, теории чисел, в естествознании, в областях прикладной математики.
Математика, в частности геометрия, представляет собой могущественный инструмент преобразования мира, в котором по словам Готфрида Харби , «нет места для некрасивой математики».

Многогранник - это такое тело, поверхность которого состоит из конечного числа плоских многоугольников.

Пример.
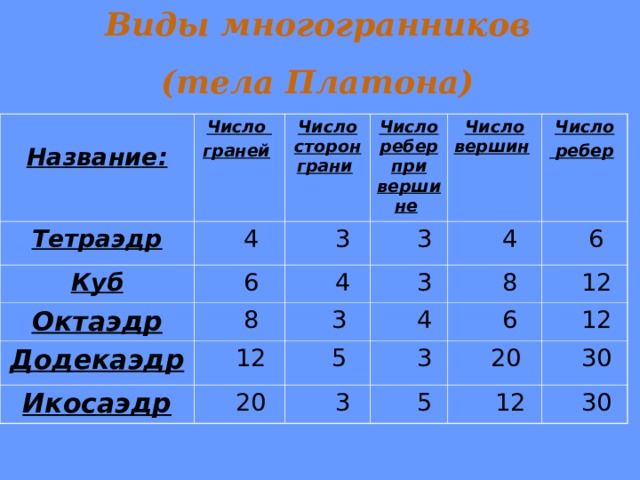
Виды многогранников
(тела Платона)
Название:
Число
граней
Тетраэдр
4
Куб
Число сторон грани
Число ребер при вершине
3
Октаэдр
6
8
3
Додекаэдр
4
Число вершин
12
3
Число
ребер
3
Икосаэдр
4
20
6
4
5
8
6
3
12
3
12
5
20
30
12
30
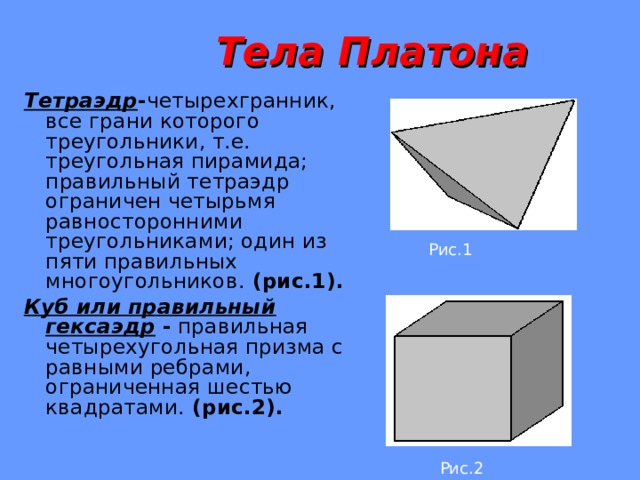
Тела Платона
Тетраэдр - четырехгранник, все грани которого треугольники, т.е. треугольная пирамида; правильный тетраэдр ограничен четырьмя равносторонними треугольниками; один из пяти правильных многоугольников. ( рис.1 ) .
Куб или правильный гексаэдр - правильная четырехугольная призма с равными ребрами, ограниченная шестью квадратами. (рис.2).
Рис.1
Рис.2
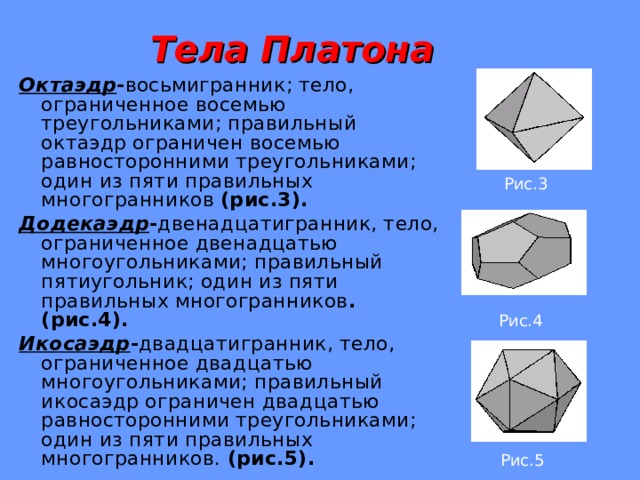
Тела Платона
Октаэдр - восьмигранник; тело, ограниченное восемью треугольниками; правильный октаэдр ограничен восемью равносторонними треугольниками; один из пяти правильных многогранников (рис.3).
Додекаэдр - двенадцатигранник, тело, ограниченное двенадцатью многоугольниками; правильный пятиугольник; один из пяти правильных многогранников . (рис.4).
Икосаэдр - двадцатигранник, тело, ограниченное двадцатью многоугольниками; правильный икосаэдр ограничен двадцатью равносторонними треугольниками; один из пяти правильных многогранников. (рис.5).
Рис.3
Рис.4
Рис.5
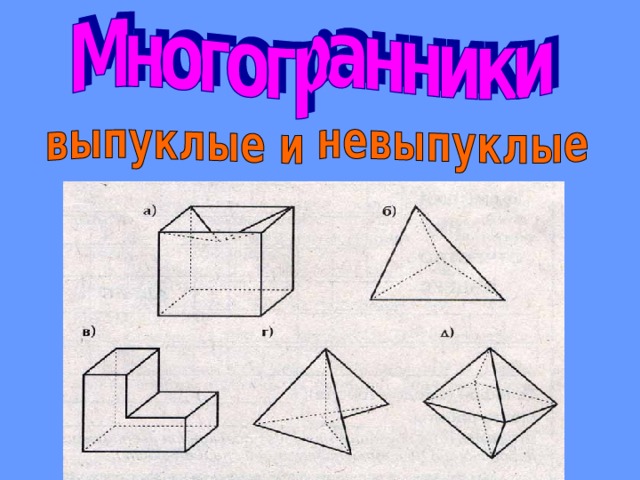

Многогранник
называется выпуклым , если он расположен по одну сторону каждого плоского многоугольника на его поверхности.


«Призма есть телесная фигура, зак-люченная между плоскостями, из которых две противоположные равны и парал-лельны, остальные же – параллелограммы» Евклид

Призма-многогранник, который состоит из двух плоских много-угольников, лежащих в разных плоскостях и совмещаемых парал-лельным переносом, и всех отрезков, соединя-ющих соответст-вующие точки этих многоугольников. Многоугольники Ф и Ф1, лежащие в параллельных плоскостях, называют основаниями призмы, а остальные грани - боковыми гранями .
Ф 1
ф
Боковые грани
18

Поверхность призмы, состоит из двух равных многоугольников (оснований) и параллелограммов (боковых граней).
Различают призмы треугольные, четырехугольные, пятиугольные и т.д. в зависимости от числа вершин основания.
Если боковое ребро призмы перпендикулярно плоскости ее основания, то такую призму называют прямой . У прямой призмы боковые грани – прямо-угольники.
Если боковое ребро призмы не перпендикулярно плоскости ее основания, то такую призму называют наклонной .
18
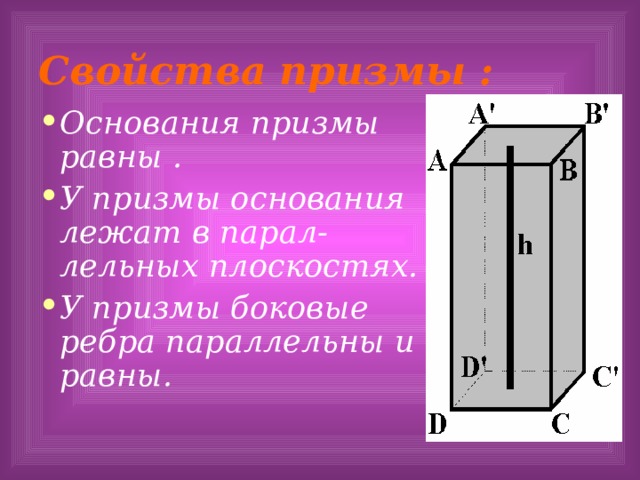
Свойства призмы :
- Основания призмы равны .
- У призмы основания лежат в парал-лельных плоскостях.
- У призмы боковые ребра параллельны и равны.
18
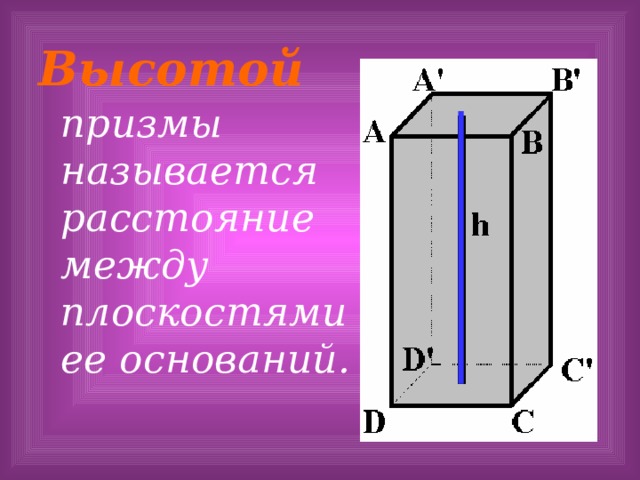
Высотой призмы называется расстояние между плоскостями ее оснований.
18

- Оказывается,что призма может быть не только геометрическим телом, но и художественным шедевром. Именно приз-ма стала основой картин Пикассо, Брака,Грисса и т.д.
18

- Оказывается, что снежинка может принять форму шестигранной призмы, но это будет зависеть от температуры воздуха.
18

Если основание призмы есть параллелограмм, то он называется параллелепипедом .
У параллелепипеда все грани - параллелограммы .
18

Слово « параллельный» происходит от греч. « па-раллелос» - идти рядом. От него уже происходят слово « параллелепипед » и др.
18

Параллелепипеды, как и призмы ,могут быть прямыми и наклонными.
Параллелепипед называется прямым , если его ребра перпендикулярны основаниям.
В противном случае параллелепипед называется наклонным
18

Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом .
У прямоугольного параллелепипеда все грани - прямоугольники .
Прямоугольный параллелепипед , у которого все ребра равны,называется кубом .
18
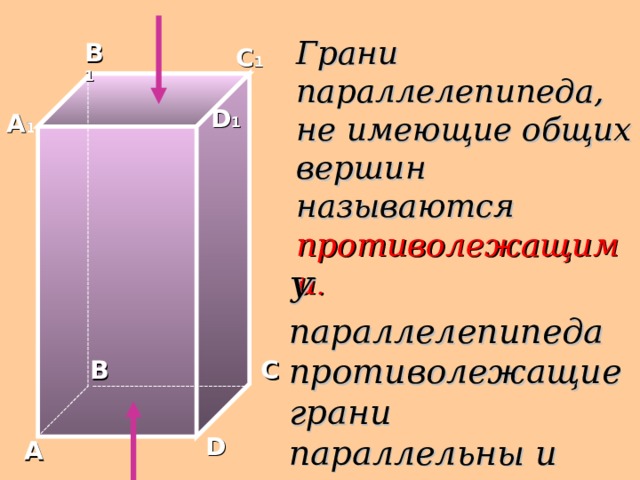
Грани параллелепипеда, не имеющие общих вершин называются противолежащими .
В 1
С 1
D 1
А 1
У параллелепипеда противолежащие грани параллельны и равны.
В
С
D
А
18
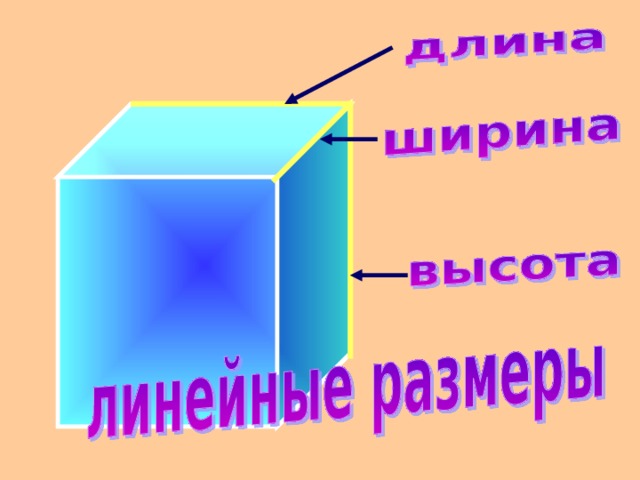
18

Диагонали параллелепипеда пересе-каются в одной точке и точкой пересечения делятся пополам.
B 1
C 1
Точка пересечения диагоналей параллелепи-педа являет-ся его цент-ром симмет-рии.
D 1
A 1
O
B
C
D
A
18
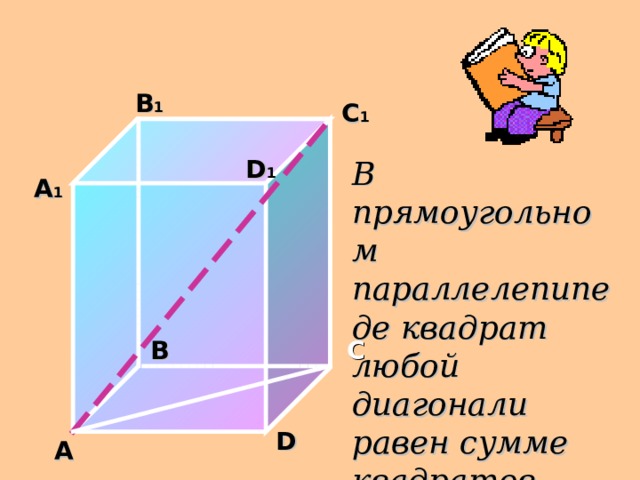
B 1
C 1
D 1
В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений .
A 1
C
B
D
A
18

Моделями прямоугольного параллелепипеда служат :
- классная комната
- кирпич
- спичечный коробок
18

- Оказывается,что кристаллы кальци-та,сколько их не дроби на более мел-кие части, всегда распадаются на осколки,имеющие форму параллелепипеда .
18

Городские здания чаще всего имеют форму многогранников.Как правило,это обычные параллелепипеды.И лишь неожиданные архитектурные решения украшают города.
18

18

Пирамида – многогранник,который состоит из плоского многоугольника – основания пирамиды, точки, не лежащей в плоскости основания, - вершины и всех отрезков, соединяющих вершину пирамиды с точками основания.
Отрезки,соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами .
18
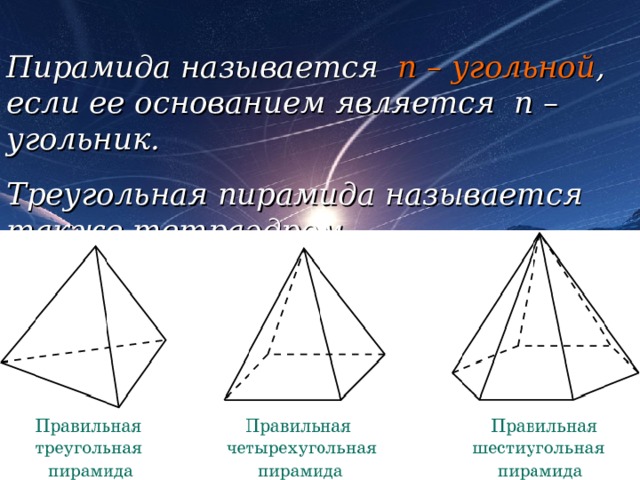
Пирамида называется n – угольной , если ее основанием является n – угольник.
Треугольная пирамида называется также тетраэдром.
18

Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
18

18

Пирамида - монументальное сооружение, имеющее геометрическую форму пирамиды. Пирамидами называются гиганские гробницы древнеегипетских фараонов, 3 - 2 тыс. до н.э.
18

Всего в Египте около сотни пирамид – больших и маленьких,ступенчатых и идеально гладких.Они расположены по берегам Нила неподалеку от древней столицы страны,в эпоху Древнего царства носящей название Мемфис. Но самые известные пирамиды Египта находятся на кромке пустынного плато Гиза на окраине Каира.Крупнейшая из них – пирамида Хеопса,второго фараона четвертой династии.Пирамида Хеопса – самое большое сооружение,когда-либо воздвигнутое человеком.
18

Основание пирамиды Хеопса представляет собой квадрат со сто-роной 227,5 метров. Высота сооружения при постройке была 146,6 метров, но в настоящее время
пирамида на 9 метров ниже: верхние камни упали во время землетрясения. Ее высота соответствует 5-этажному дому.
18

18

На строитель - ство Великой пирамиды потре - бовалось 100000 человек и 20 лет.Она была создана из более чем 2 миллионов каменных блоков,каждый из которых весил не менее 2,5 тонн.
18

18

Пирамида широко используется в повседневной жизни,даже в домашнем хозяйстве. Мы часто встречаем пирамиду на улице в виде элементов зданий или самих архитектурных построек.
18

Элементы пирамиды широко исполь-зуются в технике. Обратите внимание на компьютер, а клавиатура, кнопки– являются подобием четырехугольной усеченной пирамиды.
18

- В III веке до н. э. был построен маяк, чтобы корабли могли благо-получно миновать рифы на пути в александрий-скую бухту. Ночью им помогало в этом отражение языков пламени, а днём- столб дыма. Это был первый в мире маяк, и простоял он 1500 лет.
- Маяк был построен на маленьком острове Фарос в Средиземном море, около берегов Александрии. На его строительство ушло 20 лет, а завершён он был около 280 лет до н.э.
18

Взглянем на кристаллы.Мы обнаружим в них сочетание призм,пирамид и других многогранников.
18

18

Измерение объемов
Объемы зерновых амбаров и других сооружений в виде кубов, призм и цилиндров египтяне и вавилоняне, китайцы и индийцы вычисляли путем умножения площади основания на высоту.
Однако древнему Востоку были известны в основном только отдельные правила, найденные опытным путем, которыми пользовались для нахождения объемов для площадей фигур. В более позднее время, когда геометрия сформировалась как наука, был найден общий подход к вычислению объемов многогранников.

Основные свойства объемов
1. Равные тела имеют равные объемы.
2. Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел.
За единицу измерения объемов применяется
1мм 3 , 1см 3 , 1 м 3 .














































































