
Область определения и множество значений функции
Малыкина Елена Александровна
учитель математики
высшей квалификационной категории
«Лицея №78 им. А.С.Пушкина»

Понятие функции
Функция – это зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у.
х – независимая переменная или аргументу
y – зависимая переменная или значение функции
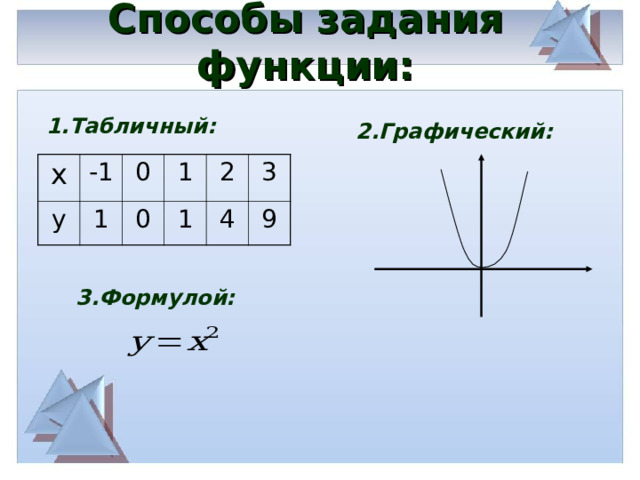
Способы задания функции:
1.Табличный:
2.Графический:
х
-1
у
1
0
1
0
1
2
4
3
9
3.Формулой:

Область определения функции
Областью определения функции называют множество всех значений, которые может принимать ее аргумент х.
Обозначение: D( f )
Область значений функции – все значения зависимой переменной у.
Обозначение: Е( f )
Если функция у = f(х) задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений х, при которых выражение f(х) имеет смысл.

Множество значений функции
Множеством значений функции называют множество всех значений которые может принимать переменная у.
Обозначение: Е (у)
![Подробное объяснение Например: f(x) = 3x2 + 6x -2 . Это квадратичная функция, и ее график – парабола . Если вам дана линейная функция или любая другая с переменной в нечетной степени, например, f(x) = 6x3+2x + 7, пропустите этот шаг. Но если вам дана квадратичная функция или любая другая с переменной х в четной степени, вы должны найти вершину графика этой функции. Для этого используйте формулу х=-b/2a.В функции 3x2 + 6x -2 a = 3, b = 6, c = -2. Вычисляем: х = -6/(2*3)= -1.[2] Теперь подставьте х= -1 в функцию, чтобы найти у. f(-1) = 3*(-1)2 + 6*(-1) -2 = 3 - 6 -2 = -5. Координаты вершины параболы (-1,-5). Нанесите ее на координатную плоскость. Точка лежит в третьем квадранте координатной плоскости. Так как член x2 положительный, то парабола будет направлена вверх.[3] f(-2) = 3(-2)2 + 6(-2) -2 = -2. первая точка на параболе (-2, -2) f(0) = 3(0)2 + 6(0) -2 = -2. Вторая точка на параболе (0,-2) f(1) = 3(1)2 + 6(1) -2 = 7. Третья точка на параболе (1, 7). Найдите наименьшее значение у на графике. Эта вершина параболы, где у=-5. Так как парабола лежит выше вершины, то множество значений функции y ≥ -5.](https://fsd.multiurok.ru/html/2023/05/28/s_6473ab3e42403/img5.jpg)
Подробное объяснение
Например: f(x) = 3x2 + 6x -2 . Это квадратичная функция, и ее график – парабола .
Если вам дана линейная функция или любая другая с переменной в нечетной степени, например, f(x) = 6x3+2x + 7, пропустите этот шаг. Но если вам дана квадратичная функция или любая другая с переменной х в четной степени, вы должны найти вершину графика этой функции. Для этого используйте формулу х=-b/2a.В функции 3x2 + 6x -2 a = 3, b = 6, c = -2. Вычисляем: х = -6/(2*3)= -1.[2]
Теперь подставьте х= -1 в функцию, чтобы найти у. f(-1) = 3*(-1)2 + 6*(-1) -2 = 3 - 6 -2 = -5.
Координаты вершины параболы (-1,-5). Нанесите ее на координатную плоскость. Точка лежит в третьем квадранте координатной плоскости.
Так как член x2 положительный, то парабола будет направлена вверх.[3]
f(-2) = 3(-2)2 + 6(-2) -2 = -2. первая точка на параболе (-2, -2)
f(0) = 3(0)2 + 6(0) -2 = -2. Вторая точка на параболе (0,-2)
f(1) = 3(1)2 + 6(1) -2 = 7. Третья точка на параболе (1, 7).
Найдите наименьшее значение у на графике. Эта вершина параболы, где у=-5. Так как парабола лежит выше вершины, то множество значений функции y ≥ -5.












![Подробное объяснение Например: f(x) = 3x2 + 6x -2 . Это квадратичная функция, и ее график – парабола . Если вам дана линейная функция или любая другая с переменной в нечетной степени, например, f(x) = 6x3+2x + 7, пропустите этот шаг. Но если вам дана квадратичная функция или любая другая с переменной х в четной степени, вы должны найти вершину графика этой функции. Для этого используйте формулу х=-b/2a.В функции 3x2 + 6x -2 a = 3, b = 6, c = -2. Вычисляем: х = -6/(2*3)= -1.[2] Теперь подставьте х= -1 в функцию, чтобы найти у. f(-1) = 3*(-1)2 + 6*(-1) -2 = 3 - 6 -2 = -5. Координаты вершины параболы (-1,-5). Нанесите ее на координатную плоскость. Точка лежит в третьем квадранте координатной плоскости. Так как член x2 положительный, то парабола будет направлена вверх.[3] f(-2) = 3(-2)2 + 6(-2) -2 = -2. первая точка на параболе (-2, -2) f(0) = 3(0)2 + 6(0) -2 = -2. Вторая точка на параболе (0,-2) f(1) = 3(1)2 + 6(1) -2 = 7. Третья точка на параболе (1, 7). Найдите наименьшее значение у на графике. Эта вершина параболы, где у=-5. Так как парабола лежит выше вершины, то множество значений функции y ≥ -5.](https://fsd.multiurok.ru/html/2023/05/28/s_6473ab3e42403/img5.jpg)



















