Презентация "Пирамида. Построение пирамиды и ее сечений."

Тема урока:

Понятие Пирамиды.Построение пирамиды и ее сечений.

Разработчик: Нигматуллина Лилия Филоритовна, учитель первой категории МОБУ СОШ д.Сахаево

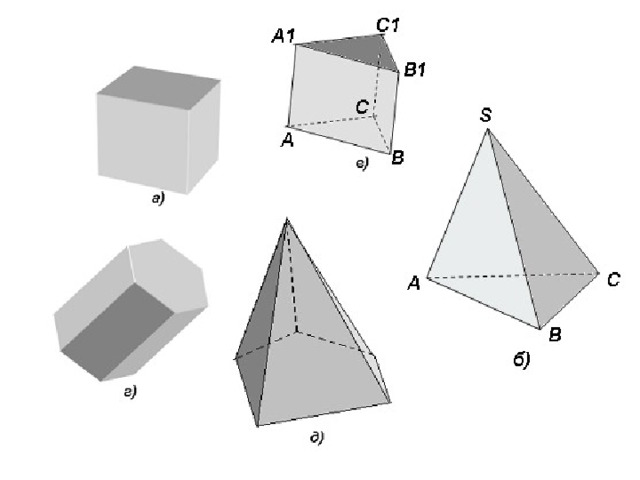
Что такое многогранник? Какие фигуры изображены на слайде?

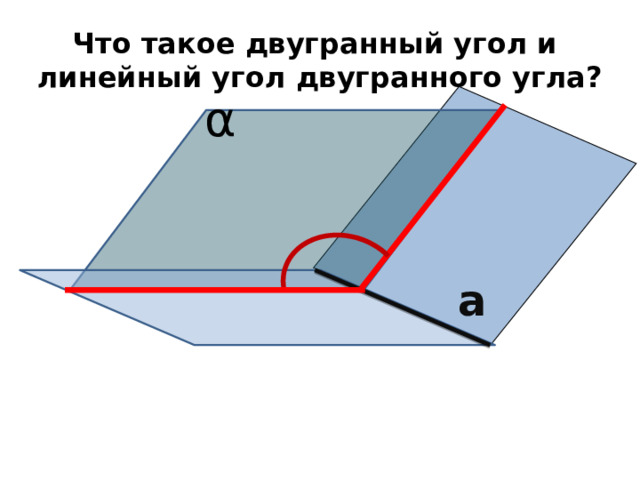
Что такое двугранный угол и линейный угол двугранного угла?

α

а

Дайте определение угла между прямой и плоскостью

а

b

α

Каким может быть расположение прямой и плоскости в пространстве?

c

d

b

a

Каким может быть расположение прямой и плоскости в пространстве?

c

a

b

А

Верно ли утверждение:

прямая , не лежащая в данной плоскости,

может пересечь ее ровно в двух точках?

Ответ: нет

Согласно исследованиям различных ученых пирамидологов таких как В.Н.Кортиков, Антуан Бови, Карел Дрбал, Александр Голод и других, в правильно соорентированных в пространстве с углами на север – юг пирамидах из неметаллических материалов (картон, бумага, дерево, камень, артстекло и др.) у людей излечивается множество болезней. Лезвии бритвы оттачиваются, заживляются раны, боли успокаиваются, выращенные овощи, фрукты в них становятся лечебными, быстрее растут цветы, продукты не только не портятся еще и становятся лечебными. Загрязненные ювелирные изделия и монеты сами собой очищаются. 

S

пирамида

B

С

K

О

А

D

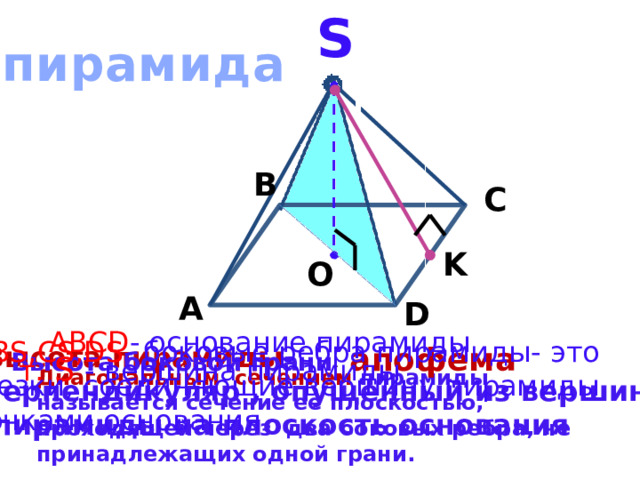
АВСD - основание пирамиды

АS,BS,CS,DS - боковые ребра пирамиды- это

отрезки, соединяющие вершину пирамиды

с точками основания

Высота пирамиды -

Высота боковой грани - апофема

перпендикуляр , опущенный из вершины

пирамиды на плоскость основания

т. S - вершина пирамиды

Диагональным сечением пирамиды называется сечение ее плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.

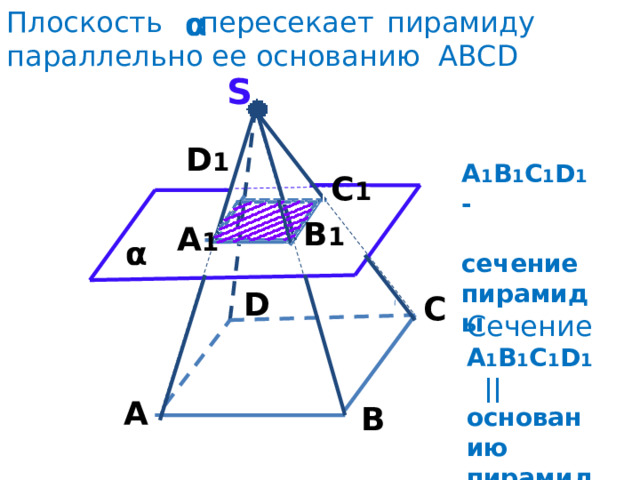
Сечение пирамиды плоскостью,

параллельной ее основанию

α

Плоскость пересекает пирамиду параллельно ее основанию ABCD

S

A 1 B 1 C 1 D 1 -

D 1

сечение пирамиды

C 1

B 1

А 1

α

Сечение A 1 B 1 C 1 D 1 ||

основанию пирамиды

D

C

А

B

Сечение четырехугольной

пирамиды плоскостью,

Проходящей через сторону

основания и точку

на одном из боковых ребер

1 случай: АВСD –параллелограмм.

S

MN II BA

N

М

D

С

А

B

2 случай:

АВCD –произвольный четырехугольник

F

D 1

T

D

A

C

B

O

Сечение пирамиды плоскостью ,

Проходящей через прямую,

лежащую в плоскости основания и точку,

лежащую на одной из боковых граней

пирамиды

S

Прямая l- след

D 1

C 1

A 1

L3

М

D

С

B 1

l

А

В

L 2

L 1

BM- является медианой, высотой и биссектрисой. Рассмотрим прямоугольный ΔBMC. По т. Пифагора вычислим сторону BM. M А C B " width="640"

Задача.

В треугольной пирамиде все ребра равны 5 см. Плоскость сечение проходит через сторону основания и середину противолежащего ребра. Найдите периметр сечения.

Решение:

D

Δ ABM – искомое сечение.

Δ DBC –равносторонний =BM-

является медианой, высотой и

биссектрисой.

Рассмотрим прямоугольный

ΔBMC. По т. Пифагора вычислим

сторону BM.

M

А

C

B

Практическая работа

S

Задание Б.

Построить сечение.

E

M

D

А

l

C

B

S

E

M

D

А

l

C

B

В 1

S

Задание Б.

Построить сечение.

M

l

А

C

B

S

Задание А.

Построить сечение.

M

l

А

C

B

S

M

l

А

C

B

Тема урока:

Пирамида.

Сечение пирамиды

плоскостями.

Спасибо!!!