Презентация по теме "Арифметические и логические основы работы компьютера", 1 курс

Арифметические и логические основы работы компьютера

Процессор выполняет арифметические и логические операции над двоичными кодами.

Поэтому для получения представления об устройстве компьютера, необходимо познакомиться с основными логическими элементами, лежащими в основе его построения.

Для понимания принципа работы таких элементов начнем это знакомство с основных начальных понятий алгебры логики.

Основные Понятия Алгебры логики

Логика — это наука о формах и способах мышления (это учение о способах рассуждений и доказательств).

Понятие — это форма мышления, которая выделяет существенные признаки предмета или класса предметов, позволяющие отличать их от других.

Пример

Прямоугольник, проливной дождь, компьютер – это понятия.

Основные Понятия Алгебры логики

Высказывание — это формулировка своего понимания окружающего мира. 

Высказывание является повествовательным предложением, в котором что-либо утверждается или отрицается.

Истинным будет высказывание, в котором связь понятий правильно отражает свойства и отношения реальных вещей. 

Ложным высказывание будет в том случае, когда оно противоречит реальной действительности.

Пример

«Буква «а» — гласная» - истинное высказывание.

«Компьютер был изобретён в середине 19 века» - ложное высказывание.

Какие из предложений являются высказываниями? Определите их истинность.

Задание.

(не является высказыванием)

1. Какой длины эта лента?

2. Делайте утреннюю зарядку!

3. Париж — столица Англии.

4.   4 + 5 = 10

5. Без труда не вытащишь и рыбку из пруда. 

6. Некоторые медведи живут на севере. 

8. Все медведи — бурые.

(не является высказыванием)

(является ложным высказыванием)

(является ложным высказыванием)

(является истинным высказыванием)

(является истинным высказыванием)

(является ложным высказыванием)

Логические выражения и операции

Алгебра логики — это наука об общих операциях, аналогичных сложению и умножению, которые выполняются над высказываниями.

Логическая переменная — это простое высказывание, содержащее только одну мысль.

Её символическое обозначение — латинская буква (например, A, B, X, Y и т. д.)

Составное высказывание — логическая функция, которая содержит несколько простых мыслей, соединённых между собой с помощью логических операций. 

Её символическое обозначение — F(A, B,…). На основе простых высказываний могут быть построены составные высказывания .

Логические выражения и операции

Логические операции — логическое действие.

Таблица истинности — таблица, определяющая значение сложного высказывания при всех возможных значениях простых высказываний.

Базовые логические операции:

• конъюнкция,
• дизъюнкция,
• отрицание (инверсия).

и дополнительные

— импликация и эквиваленция.

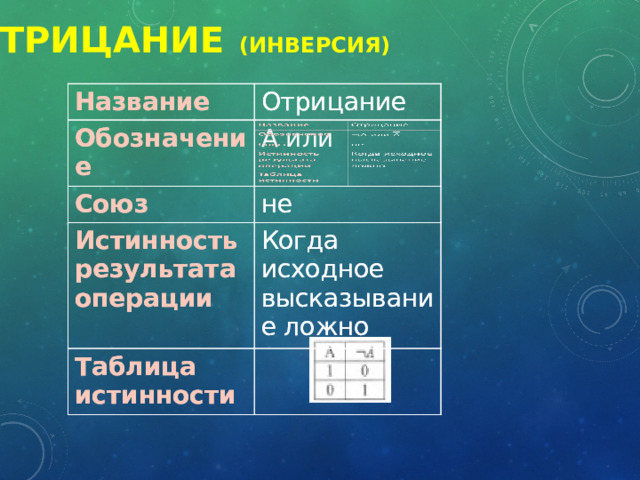
Отрицание (инверсия)

Название

Название

Отрицание

Обозначение

Отрицание

Обозначение

А или

Союз

Союз

Истинность результата операции

не

Истинность результата операции

не

Таблица истинности

Когда исходное высказывание ложно

Когда исходное высказывание ложно

Таблица истинности

Конъюнкция

Название

Название

Логическое умножение

Обозначение

Логическое умножение

Обозначение

А ^ В или

Союз

Союз

Истинность результата операции

И

Истинность результата операции

И

Таблица истинности

Таблица истинности

Когда истины одновременно оба высказывания

Когда истины одновременно оба высказывания

дизъюнкция

Название

Логическое сложение

Обозначение

А V В

Союз

ИЛИ

Истинность результата операции

Когда истинно А, либо В, либо одновременно

Таблица истинности

При построении таблиц истинности есть определенная последовательность действий

1. Определить количество строк в таблице: 

количество строк = 2 n +1,  где n – количество логических переменных.

2. Определить количество столбцов в таблице: 

количество столбцов = количеству логических переменных + количество логических операций.

3. Построить таблицу истинности с указанным количеством строк и столбцов, ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов (¬, &, V);

приоритеты: ( ), ¬, &, V.

4. Заполнить столбцы входных переменных наборами значений.

5. Заполнить таблицу истинности, выполняя логические операции в соответствии с приоритетами действий.

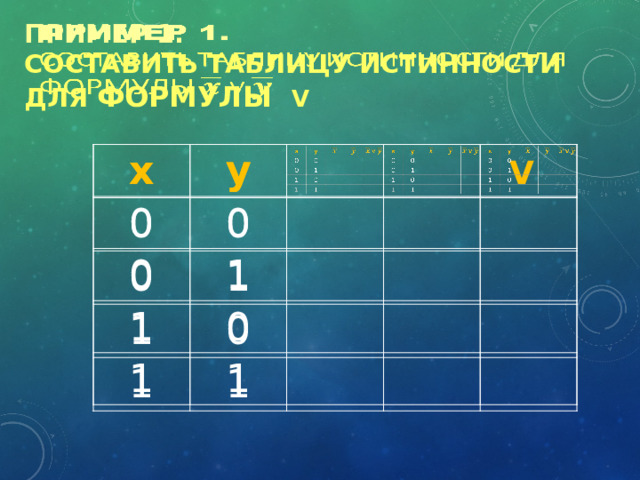
пример 1. Составить таблицу истинности для формулы V

x

x

y

y

0

0

0

0

0

0

1

1

1

1

0

1

1

V

0

1

1

Решить задачи:

Составить таблицы истинности для следующих формул:

• x &
• ¬(A&B)
• В&(АVВ)  
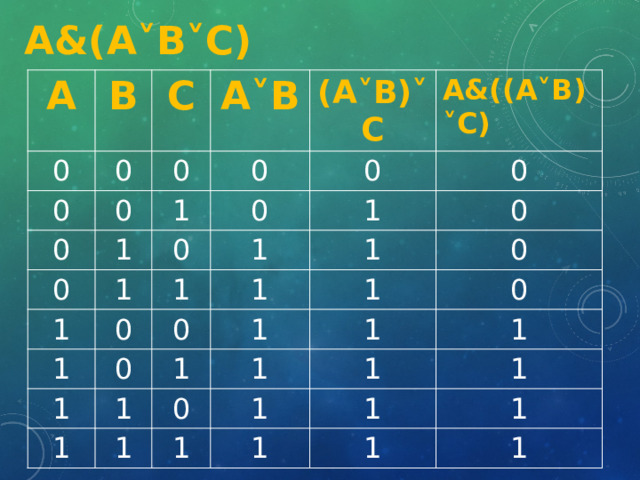
• А&(A˅B˅C)

А&(A˅B˅C)

А

В

0

С

0

0

A˅B

0

0

0

(A˅B)˅C

1

1

0

0

А&((A˅B)˅C)

1

1

1

0

1

0

0

1

1

1

1

0

1

1

А&(A˅B˅C)

А

0

В

0

0

С

0

A˅B

0

0

0

1

(A˅B)˅C

1

0

А&((A˅B)˅C)

0

0

0

1

1

1

0

1

1

0

1

0

1

1

0

1

0

0

1

1

1

1

1

1

1

1

0

0

1

1

1

1

1

1

1

1

1

1

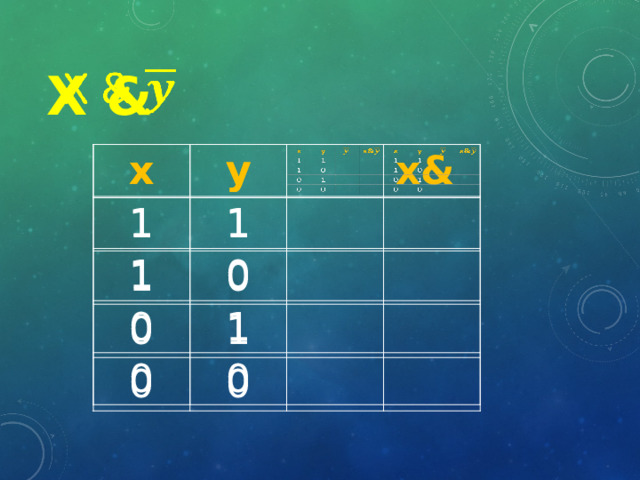
x &

x

x

y

1

1

y

1

1

1

1

0

0

0

0

x&

1

1

0

0

0

0