Презентация по теме "Четные и нечетные функции"

Четные и нечетные функции

Цели урока:

1.Изучить определение четной и нечетной функций

2.Научить определять четность функций, заданных формулой

2.Научить распознавать графики четных нечетных функций

Определение четной функции

• Функция у = f (х) называется четной , если ее область определения симметрична относительно начала координат и для любого х из области определения функции выполняется равенство

f (- х) = f (x).

Определение нечетной функции

• Функция у = f (х) называется нечетной , если ее область определения симметрична относительно начала координат и для любого х из области определения функции выполняется равенство
• f (- x) = - f (x).

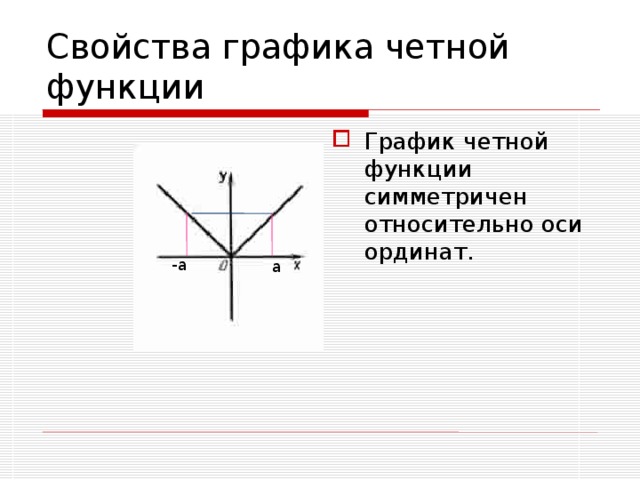
Свойства графика четной функции

• График четной функции симметричен относительно оси ординат.

-а

а

-a

Свойства графика нечетной функции

• График нечетной функции симметричен относительно начала координат.

-а

а

а

Доказательство четности

• f(x)=x 4
• 1 . Область определения D(f)=R , симметрична относительно начала координат.
• 2. f(-x)=(-x) 4 =x 4 =f(x) , значит f(x) – четная функция

Доказательство нечетности

• f(x)=x 3
• 1 . Область определения D(f)=R , симметрична относительно начала координат.
• 2. f(-x)=(-x) 3 = - x 3 = - f(x) , значит f(x) – нечетная функция

• f(x)=x 7 cos5x
• 1.D(x)=R
• 2.f(-x)=(-x) 7 cos(5(-x))= -x 7 cos5x=-f(x), значит f(x) – нечетная функция

Если данные условия четности или нечетности не выполняются, то говорят, что функция f(x) не является ни четной ни нечетной.

Исследуйте функции на четность

• 1 группа
• f(x)=Cosx+2x 2
• f(x)=x 5 +6x
• f(x)=x+Cosx

• 2 группа
• f(x)=Sinx+2x 3
• f(x)=x 4 +5
• f(x)=x 3 +Cosx

Проверьте результаты исследования

• 1 группа
• f(x)= с osx+2x 2 четная функция
• f(x)=x 5 +6x – нечетная функция
• f(x)=x+ с osx - функция не является ни четной ни нечетной

• 2 группа
• f(x)=Sinx+2x 3 нечетная функция
• f(x)=x 4 +5 - четная функция
• f(x)=x 3 + с osx - функция не является ни четной ни нечетной