
Объёмы тел вращения. Объём конуса. Объём усеченного конуса.
Данную работу выполнили: Каторкина Елизавета
Жулина Елизавета
Ученицы 11 «Б» класса
Руководитель: Мартынова Екатерина Владимировна
Определение конуса и его виды
- Конус — это тело, получающееся при вращении прямоугольного треугольника вокруг прямой, содержащей один из его катетов.
- Основание конуса - это плоскость, образованная в результате пересечения плоской поверхности и всех лучей, исходящих из вершины конуса. У конуса могут быть такие основы, как круг, эллипс, гипербола и парабола.
- Образующей конуса (L) называется любой отрезок, который соединяет вершину конуса с границей основания конуса.
- Образующая есть отрезок луча, выходящего из вершины конуса. Длина образующей (L) прямого кругового конуса через радиус R и высоту H (через теорему Пифагора): L 2 = R 2 + H 2
- Направляющая конуса - это кривая, которая описывает контур основания конуса.
- Боковая поверхность конуса - это совокупность всех образующих конуса. То есть, поверхность, которая образуется движением образующей по направляющей конуса.
- Поверхность конуса состоит из боковой поверхности и основания конуса.
- Высота конуса (H) - это отрезок, который выходит из вершины конуса и перпендикулярный к его основанию.
- Ось конуса (a) - это прямая, проходящая через вершину конуса и центр основания конуса.
- Осевое сечение конуса - это сечение конуса плоскостью, проходящей через ось конуса. Такое сечение образует равнобедренный треугольник, у которого стороны образованы образующими, а основание треугольника - это диаметр основания конуса.
- Касательная плоскость к конусу - это плоскость, проходящая через образующую конуса и перпендикулярна к осевому сечению конуса.

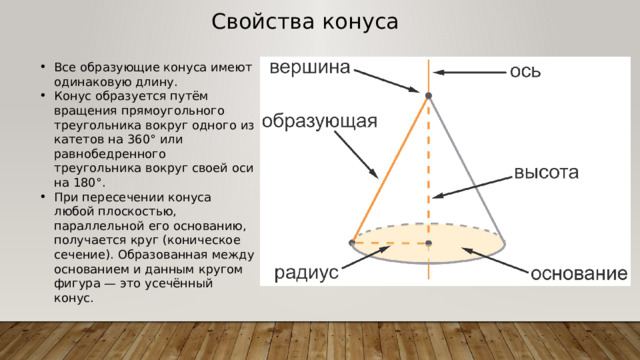
Свойства конуса
- Все образующие конуса имеют одинаковую длину.
- Конус образуется путём вращения прямоугольного треугольника вокруг одного из катетов на 360° или равнобедренного треугольника вокруг своей оси на 180°.
- При пересечении конуса любой плоскостью, параллельной его основанию, получается круг (коническое сечение). Образованная между основанием и данным кругом фигура — это усечённый конус.

Формулы вычисления площадей конуса. Формула нахождения объёма конуса
Площадь боковой поверхности (S b ) прямого конуса через радиус R и длину образующей L:
S b = πRL
Общая площадь поверхности (S p ) прямого кругового конуса через радиус R и длину образующей L:
S p = πRL + πR 2
Чтобы найти объём конуса с высотой, равной h , и радиусом основания r вычисляют по формуле:
V = πr 2 h
Заметим, что πr 2 = S , где S – площадь основания конуса. Поэтому объём конуса с высотой, равной h , и основанием,
площадь которой равна S , вычисляют по формуле:
V = Sh

5 см
Приступим к решению задач
Найдите объём конуса, радиус основания которого равен 6 см, а высота – 5 см.
В
Решение:
Дано:
V = πr 2 h
Конус
V= π×6 2 ×5= 60π см 3
ОА=6 см(r)
ВО=5 см(h)
Найти:
V - ?
ОТВЕТ: 60π см 3
А
6 см
О

? см
Найдите высоту конуса, объём которого равен 24π см 3 , а радиус основания – 3 см.
Решение:
Дано:
V=πr 2 h
Конус
h =
V= 24π см 3
ОА= 3 см (r)
h = = 8 см
Найти:
ВО(h) - ?
ОТВЕТ: ВО(h) = 8 см
3 см
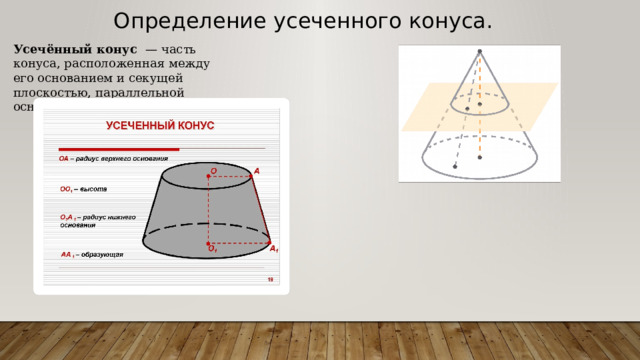
Определение усеченного конуса.
Усечённый конус — часть конуса, расположенная между его основанием и секущей плоскостью, параллельной основанию.
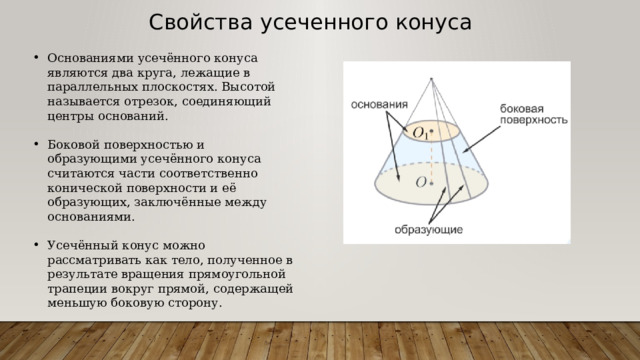
Свойства усеченного конуса
- Основаниями усечённого конуса являются два круга, лежащие в параллельных плоскостях. Высотой называется отрезок, соединяющий центры оснований.
- Боковой поверхностью и образующими усечённого конуса считаются части соответственно конической поверхности и её образующих, заключённые между основаниями.
- Усечённый конус можно рассматривать как тело, полученное в результате вращения прямоугольной трапеции вокруг прямой, содержащей меньшую боковую сторону.
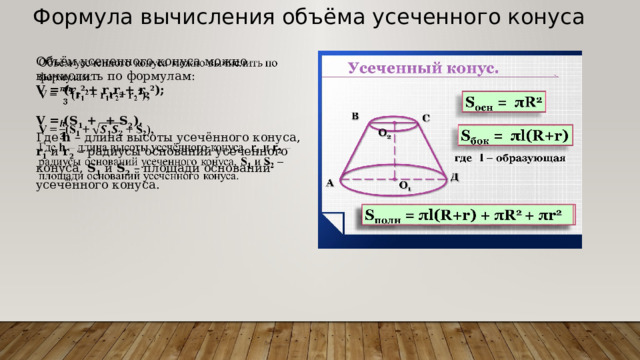
Формула вычисления объёма усеченного конуса
Объём усеченного конуса можно вычислить по формулам:
V = (r 1 2 + r 1 r 2 + r 2 2 );
V = (S 1 + + S 2 ),
Где h – длина высоты усечённого конуса, r 1 и r 2 – радиусы оснований усеченного конуса, S 1 и S 2 – площади оснований усечённого конуса.
 АЕ = AD – BC = 14 – 8 = 6 см. Рассмотрим ∆АВЕ – прямоугольный, т.к. ВЕ – высота треугольник равнобедренный = AE = BE = = 6 cм. 2. V = (r 1 2 + r 1 r 2 + r 2 2 ) V = (14 2 + 14×8 + 8 2 ) = 2π(196 + 112+ 64) = 744π cм 3 O 1 Дано: усечённый конус AD – 14 см(r 1 ) BC – 8 см(r 2 ) C В Найти: V - ? 45˚ А D E О ОТВЕТ: 744π см 3 " width="640"
АЕ = AD – BC = 14 – 8 = 6 см. Рассмотрим ∆АВЕ – прямоугольный, т.к. ВЕ – высота треугольник равнобедренный = AE = BE = = 6 cм. 2. V = (r 1 2 + r 1 r 2 + r 2 2 ) V = (14 2 + 14×8 + 8 2 ) = 2π(196 + 112+ 64) = 744π cм 3 O 1 Дано: усечённый конус AD – 14 см(r 1 ) BC – 8 см(r 2 ) C В Найти: V - ? 45˚ А D E О ОТВЕТ: 744π см 3 " width="640"
Приступим к решению задачи
Найдите объём усечённого конуса, радиусы оснований которого равны 8 см и 14 см, а угол
между его образующей и плоскостью большего основания равен 45˚.
Решение:
- Найдем АЕ в усечённом конусе.
Т.к. АВСD – равнобедренная трапеция =
АЕ = AD – BC = 14 – 8 = 6 см.
Рассмотрим ∆АВЕ – прямоугольный, т.к. ВЕ – высота
треугольник равнобедренный = AE = BE = = 6 cм.
2. V = (r 1 2 + r 1 r 2 + r 2 2 )
V = (14 2 + 14×8 + 8 2 ) = 2π(196 + 112+ 64) = 744π cм 3
O 1
Дано:
усечённый конус
AD – 14 см(r 1 )
BC – 8 см(r 2 )
C
В
Найти:
V - ?
45˚
А
D
E
О
ОТВЕТ: 744π см 3

Благодарим за внимание!














 АЕ = AD – BC = 14 – 8 = 6 см. Рассмотрим ∆АВЕ – прямоугольный, т.к. ВЕ – высота треугольник равнобедренный = AE = BE = = 6 cм. 2. V = (r 1 2 + r 1 r 2 + r 2 2 ) V = (14 2 + 14×8 + 8 2 ) = 2π(196 + 112+ 64) = 744π cм 3 O 1 Дано: усечённый конус AD – 14 см(r 1 ) BC – 8 см(r 2 ) C В Найти: V - ? 45˚ А D E О ОТВЕТ: 744π см 3 " width="640"
АЕ = AD – BC = 14 – 8 = 6 см. Рассмотрим ∆АВЕ – прямоугольный, т.к. ВЕ – высота треугольник равнобедренный = AE = BE = = 6 cм. 2. V = (r 1 2 + r 1 r 2 + r 2 2 ) V = (14 2 + 14×8 + 8 2 ) = 2π(196 + 112+ 64) = 744π cм 3 O 1 Дано: усечённый конус AD – 14 см(r 1 ) BC – 8 см(r 2 ) C В Найти: V - ? 45˚ А D E О ОТВЕТ: 744π см 3 " width="640"




















