Презентация по теме "Объем пирамиды"

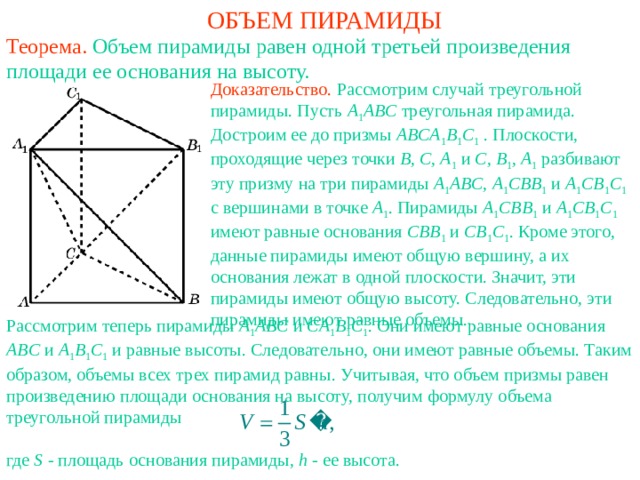
ОБЪЕМ ПИРАМИДЫ

Теорема. Объем пирамиды равен одной третьей произведения площади ее основания на высоту.

Доказательство. Рассмотрим случай треугольной пирамиды. Пусть A 1 ABC треугольная пирамида. Достроим ее до призмы ABCA 1 B 1 C 1 . Плоскости, проходящие через точки B , C , A 1 и C , B 1 , A 1 разбивают эту призму на три пирамиды A 1 ABC , A 1 CBB 1 и A 1 CB 1 C 1 с вершинами в точке A 1 . Пирамиды A 1 CBB 1 и A 1 CB 1 C 1 имеют равные основания CBB 1 и CB 1 C 1 . Кроме этого, данные пирамиды имеют общую вершину, а их основания лежат в одной плоскости. Значит, эти пирамиды имеют общую высоту. Следовательно, эти пирамиды имеют равные объемы.

Рассмотрим теперь пирамиды A 1 ABC и CA 1 B 1 C 1 . Они имеют равные основания ABC и A 1 B 1 C 1 и равные высоты. Следовательно, они имеют равные объемы. Таким образом, объемы всех трех пирамид равны. Учитывая, что объем призмы равен произведению площади основания на высоту, получим формулу объема треугольной пирамиды

где S - площадь основания пирамиды, h - ее высота.

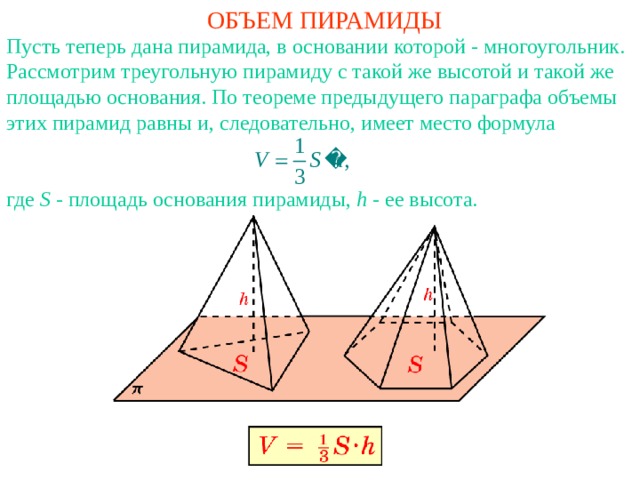
ОБЪЕМ ПИРАМИДЫ

Пусть теперь дана пирамида, в основании которой - многоугольник. Рассмотрим треугольную пирамиду с такой же высотой и такой же площадью основания. По теореме предыдущего параграфа объемы этих пирамид равны и, следовательно, имеет место формула

где S - площадь основания пирамиды, h - ее высота.

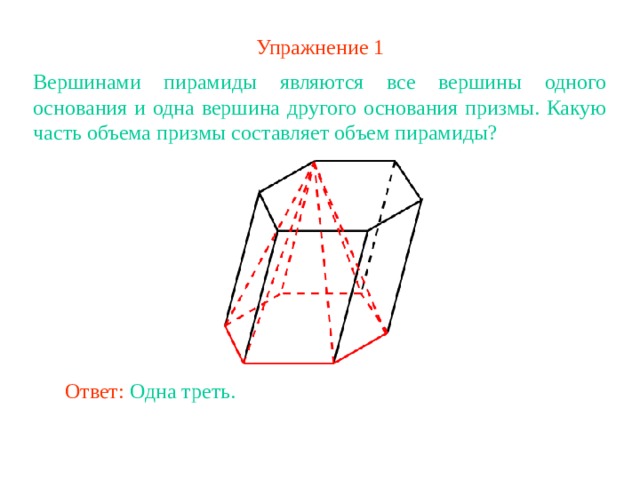
Упражнение 1

Вершинами пирамиды являются все вершины одного основания и одна вершина другого основания призмы. Какую часть объема призмы составляет объем пирамиды?

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: Одна треть .

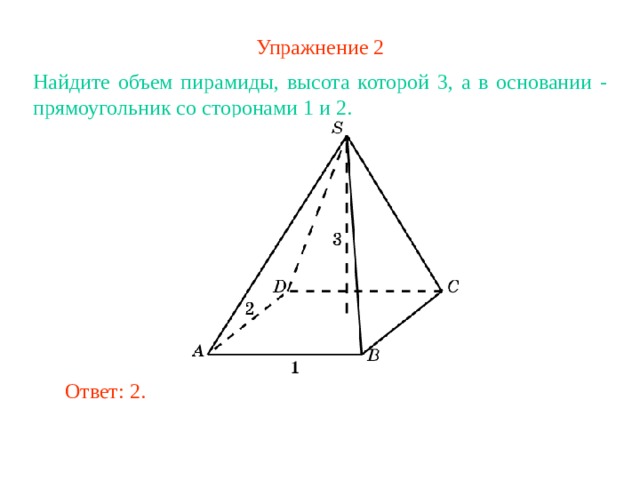
Упражнение 2

Найдите объем пирамиды, высота которой 3 , а в основании - прямоугольник со сторонами 1 и 2 .

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: 2.

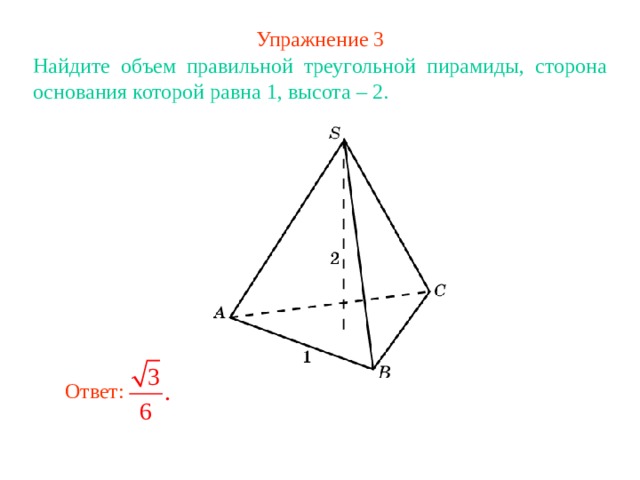
Упражнение 3

Найдите объем правильной треугольной пирамиды, сторона основания которой равна 1 , высота – 2 .

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

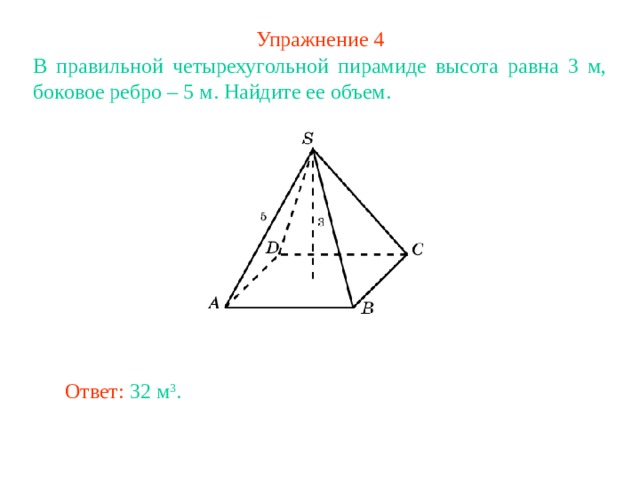
Упражнение 4

В правильной четырехугольной пирамиде высота равна 3 м, боковое ребро – 5 м. Найдите ее объем.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: 32 м 3 .

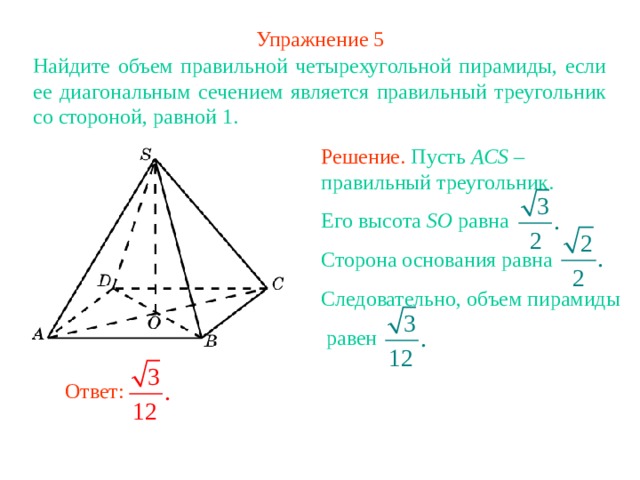
Упражнение 5

Найдите объем правильной четырехугольной пирамиды, если ее диагональным сечением является правильный треугольник со стороной, равной 1.

Решение. Пусть ACS – правильный треугольник.

Его высота SO равна

Сторона основания равна

Следовательно, объем пирамиды

равен

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

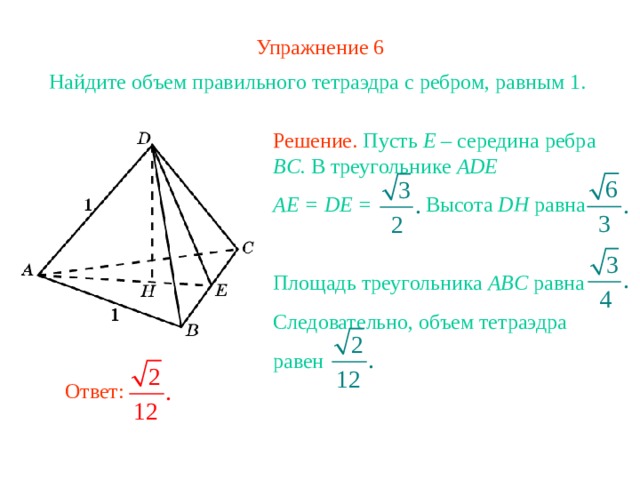
Упражнение 6

Найдите объем правильного тетраэдра с ребром, равным 1.

Решение. Пусть E – середина ребра BC. В треугольнике ADE

AE = DE = Высота DH равна

Площадь треугольника ABC равна

Следовательно, объем тетраэдра

равен

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

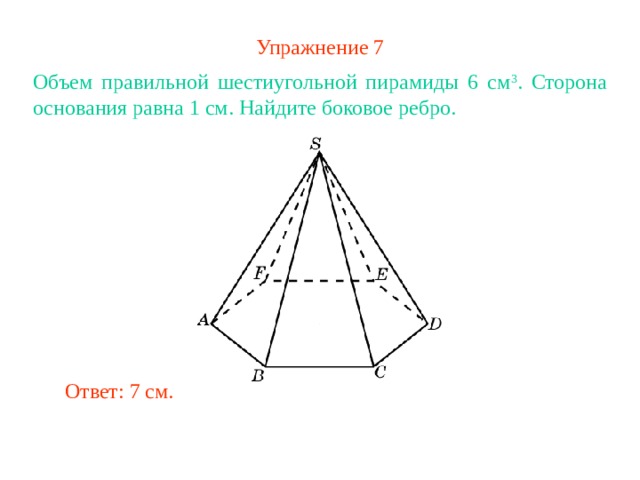
Упражнение 7

Объем правильной шестиугольной пирамиды 6 см 3 . Сторона основания равна 1 см. Найдите боковое ребро.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: 7 см.

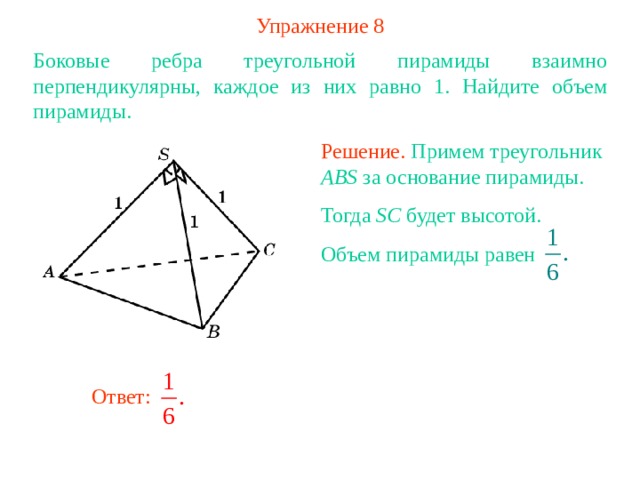
Упражнение 8

Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 1 . Найдите объем пирамиды.

Решение. Примем треугольник ABS за основание пирамиды.

Тогда SC будет высотой.

Объем пирамиды равен

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

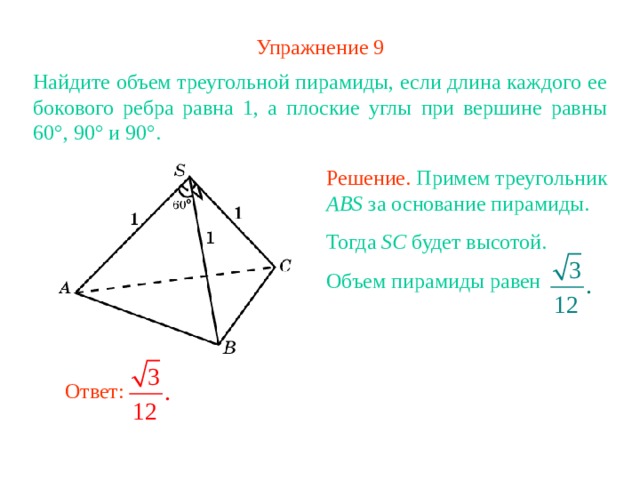
Упражнение 9

Найдите объем треугольной пирамиды, если длина каждого ее бокового ребра равна 1 , а плоские углы при вершине равны 60°, 90° и 90°.

Решение. Примем треугольник ABS за основание пирамиды.

Тогда SC будет высотой.

Объем пирамиды равен

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

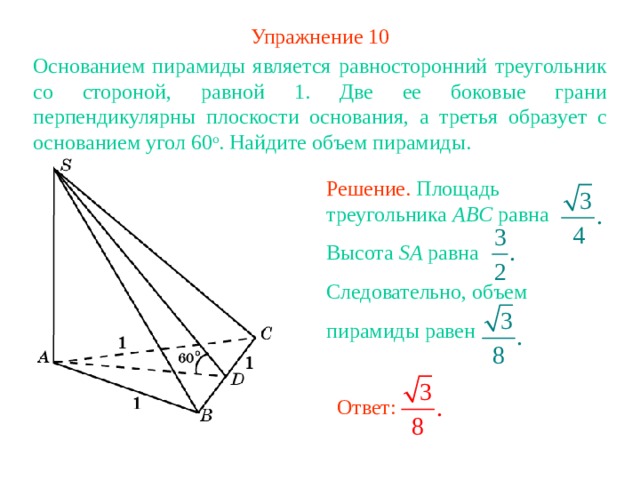
Упражнение 10

Основанием пирамиды является равносторонний треугольник со стороной, равной 1. Две ее боковые грани перпендикулярны плоскости основания, а третья образует с основанием угол 60 о . Найдите объем пирамиды.

Решение. Площадь треугольника ABC равна

Высота SA равна

Следовательно, объем

пирамиды равен

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

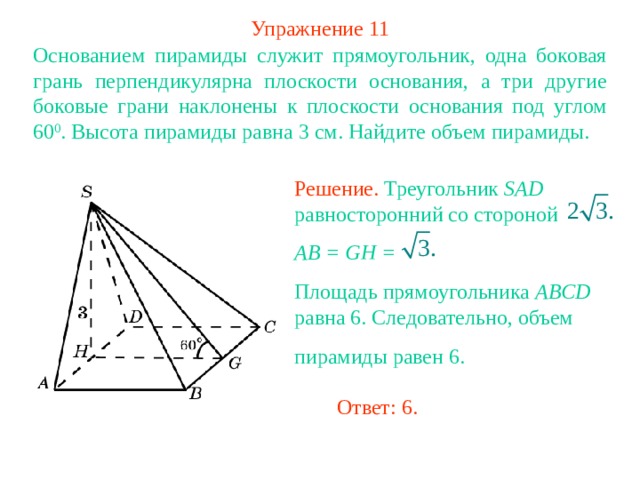
Упражнение 11

Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60 0 . Высота пирамиды равна 3 см. Найдите объем пирамиды.

Решение. Треугольник SAD равносторонний со стороной

AB = GH =

Площадь прямоугольника ABCD равна 6. Следовательно, объем

пирамиды равен 6.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: 6.

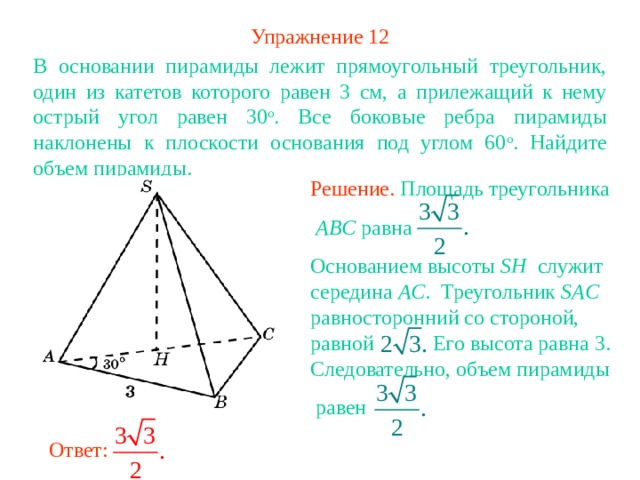
Упражнение 12

В основании пирамиды лежит прямоугольный треугольник, один из катетов которого равен 3 см, а прилежащий к нему острый угол равен 30 о . Все боковые ребра пирамиды наклонены к плоскости основания под углом 60 о . Найдите объем пирамиды.

Решение. Площадь треугольника

ABC равна

Основанием высоты SH служит середина AC . Треугольник SAC равносторонний со стороной, равной Его высота равна 3. Следовательно, объем пирамиды

равен

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

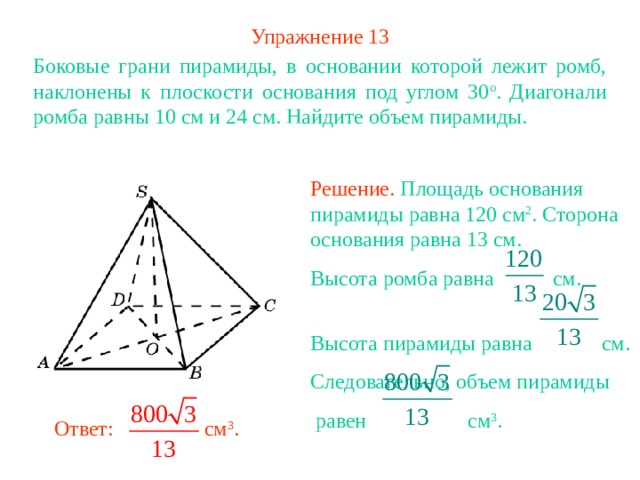
Упражнение 13

Боковые грани пирамиды, в основании которой лежит ромб, наклонены к плоскости основания под углом 30 о . Диагонали ромба равны 10 см и 24 см. Найдите объем пирамиды.

Решение. Площадь основания пирамиды равна 120 см 2 . Сторона основания равна 13 см.

Высота ромба равна см.

Высота пирамиды равна см.

Следовательно, объем пирамиды

равен см 3 .

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: см 3 .

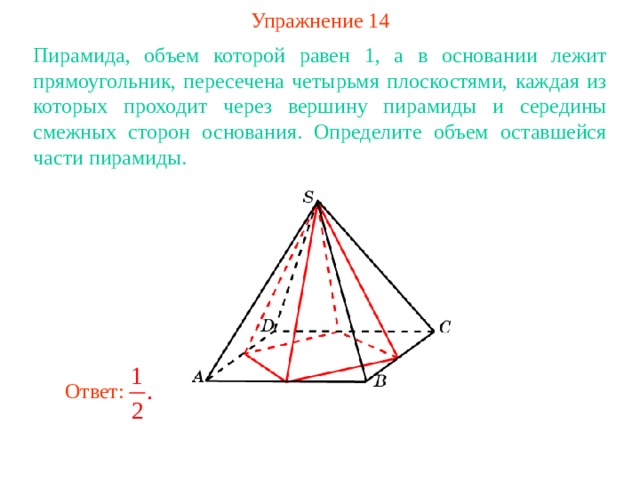
Упражнение 14

Пирамида, объем которой равен 1 , а в основании лежит прямоугольник, пересечена четырьмя плоскостями, каждая из которых проходит через вершину пирамиды и середины смежных сторон основания. Определите объем оставшейся части пирамиды.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

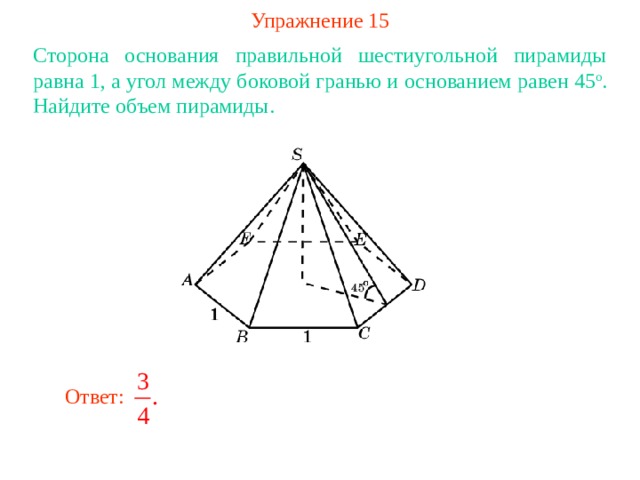
Упражнение 15

Сторона основания правильной шестиугольной пирамиды равна 1 , а угол между боковой гранью и основанием равен 45 о . Найдите объем пирамиды.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

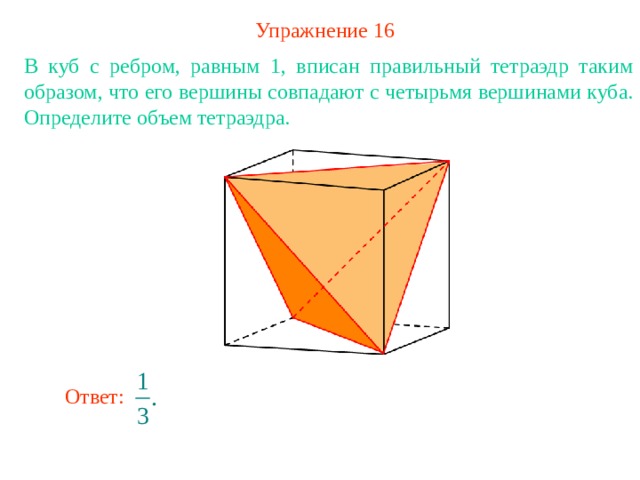
Упражнение 16

В куб с ребром, равным 1, вписан правильный тетраэдр таким образом, что его вершины совпадают с четырьмя вершинами куба. Определите объем тетраэдра.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

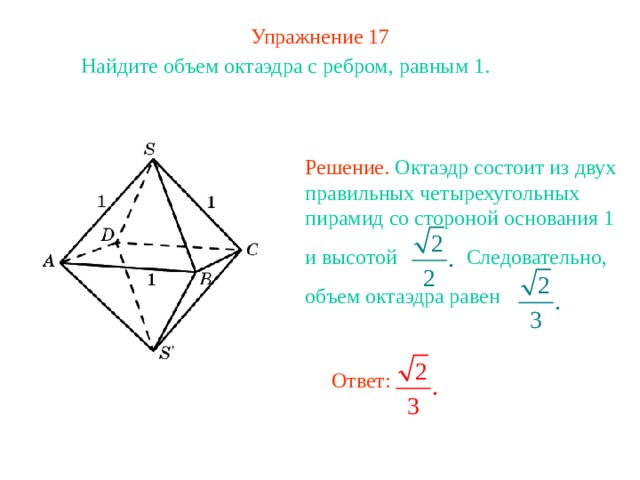
Упражнение 17

Найдите объем октаэдра с ребром, равным 1.

Решение. Октаэдр состоит из двух правильных четырехугольных пирамид со стороной основания 1

и высотой Следовательно,

объем октаэдра равен

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

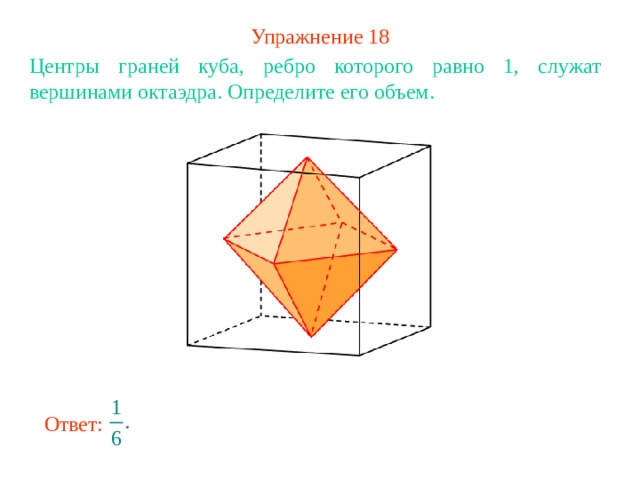
Упражнение 18

Центры граней куба, ребро которого равно 1, служат вершинами октаэдра. Определите его объем.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

Упражнение 19

Развертка треугольной пирамиды представляет собой квадрат со стороной 1 . Найдите объем этой пирамиды.

Решение. Основанием пирамиды будет прямоугольный треугольник ABC с катетами, равными 0,5. Высота пирамиды будет равна стороне квадрата. Следовательно,

объем пирамиды равен

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

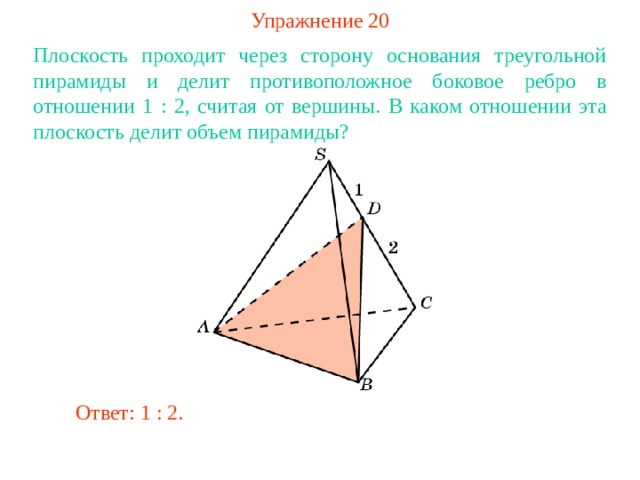
Упражнение 20

Плоскость проходит через сторону основания треугольной пирамиды и делит противоположное боковое ребро в отношении 1 : 2, считая от вершины . В каком отношении эта плоскость делит объем пирамиды?

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: 1 : 2.

Упражнение 21

Плоскость пересекает ребра SA , SB , SC треугольной пирамиды SABC в точках A ’, B ’, C ’ соответственно. Найдите объем пирамиды SA ’ B ’ C ’ , если объем исходной пирамиды равен 1 и SA ’ : SA = 1 : 2, SB ’ : SB = 2 : 3, SC ’ : SC = 3 : 4.

Решение. Площадь треугольника SA’B’ составляет 1 / 3 площади треугольника SAB . Высота, опущенная из точки C’ составляет 3 /4 высоты, опущенной из вершины С . Следовательно, объем пирамиды SA’B’C’ равен 1 /4 .

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: 1/4 .

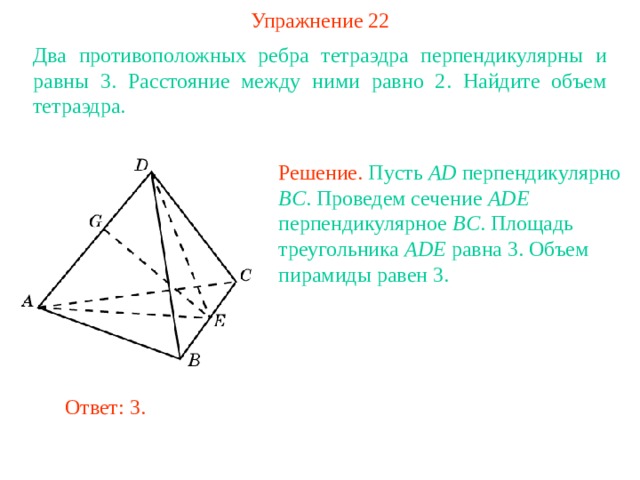
Упражнение 22

Два противоположных ребра тетраэдра перпендикулярны и равны 3. Расстояние между ними равно 2. Найдите объем тетраэдра.

Решение. Пусть AD перпендикулярно BC . Проведем сечение ADE перпендикулярное BC . Площадь треугольника ADE равна 3. Объем пирамиды равен 3.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: 3.

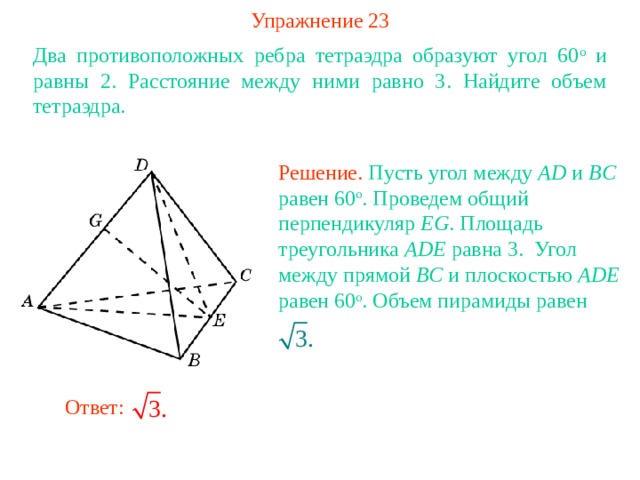
Упражнение 23

Два противоположных ребра тетраэдра образуют угол 60 о и равны 2. Расстояние между ними равно 3. Найдите объем тетраэдра.

Решение. Пусть угол между AD и BC равен 60 о . Проведем общий перпендикуляр EG . Площадь треугольника ADE равна 3. Угол между прямой BC и плоскостью ADE равен 60 о . Объем пирамиды равен

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

Упражнение 24

Одно ребро тетраэдра равно 6. Все остальные ребра равны 4. Найдите объем тетраэдра.

Решение. Пусть BC = 6. Обозначим E середину BC . AE = DE = Высота EG треугольника ADE равна Его площадь равна Объем пирамиды равен

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

Упражнение 25

Два куба с ребрами a имеют общую диагональ, но один повернут вокруг этой диагонали на угол 60° по отношению к другому. Найдите объем их общей части.

Ответ: Общая часть является правильной 6-й бипирамидой со стороной основания и

Высотой Объем этой

бипирамиды равен

В режиме слайдов ответ появляется после кликанья мышкой

Упражнение 26

Два правильных тетраэдра с ребрами a имеют общую высоту. Один из них повернут на 60° по отношению к другому. Найдите объем их общей части.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

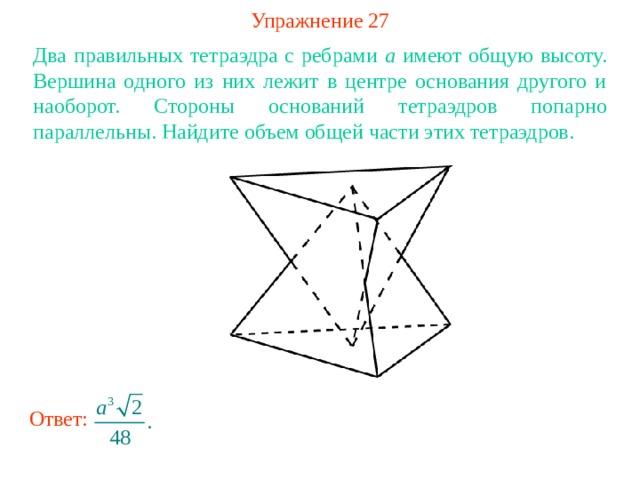
Упражнение 27

Два правильных тетраэдра с ребрами a имеют общую высоту. Вершина одного из них лежит в центре основания другого и наоборот. Стороны оснований тетраэдров попарно параллельны. Найдите объем общей части этих тетраэдров.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

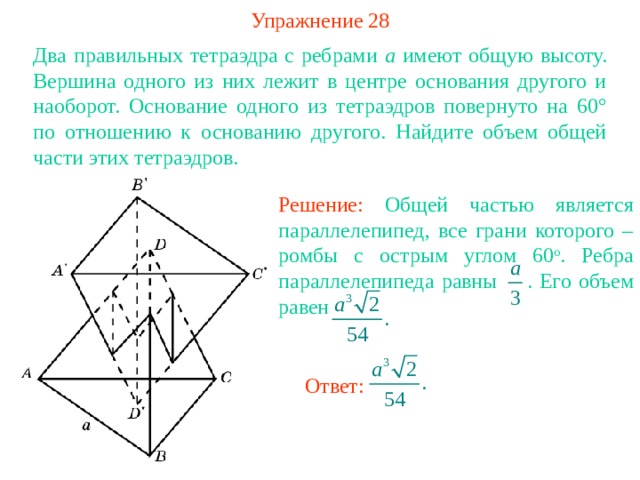
Упражнение 28

Два правильных тетраэдра с ребрами a имеют общую высоту. Вершина одного из них лежит в центре основания другого и наоборот. Основание одного из тетраэдров повернуто на 60° по отношению к основанию другого. Найдите объем общей части этих тетраэдров.

Решение: Общей частью является параллелепипед, все грани которого – ромбы с острым углом 60 о . Ребра параллелепипеда равны . Его объем равен

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

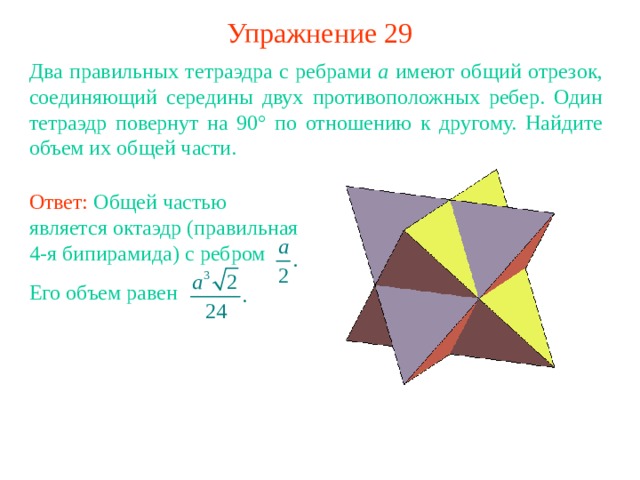
Упражнение 29

Два правильных тетраэдра с ребрами a имеют общий отрезок, соединяющий середины двух противоположных ребер. Один тетраэдр повернут на 90° по отношению к другому. Найдите объем их общей части.

Ответ: Общей частью является октаэдр (правильная 4-я бипирамида) с ребром

Его объем равен

В режиме слайдов ответ появляется после кликанья мышкой

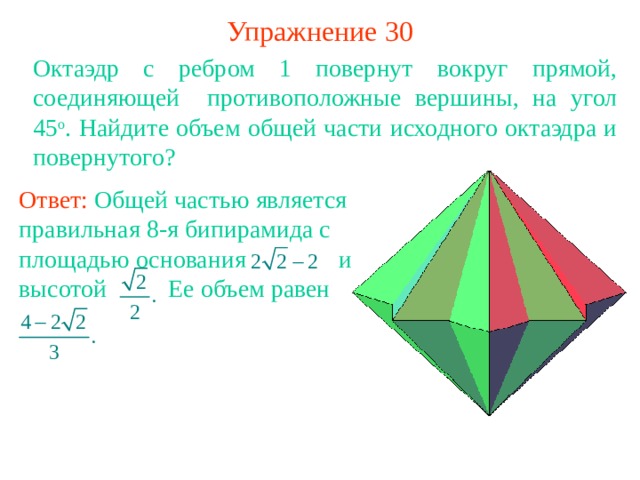
Упражнение 30

Октаэдр с ребром 1 повернут вокруг прямой, соединяющей противоположные вершины, на угол 45 о . Найдите объем общей части исходного октаэдра и повернутого?

Ответ: Общей частью является правильная 8-я бипирамида с площадью основания и высотой Ее объем равен

В режиме слайдов ответ появляется после кликанья мышкой