Презентация по теме: "Парабола, координаты вершины параболы, ось симметрии", Алгебра, 9 класс

Парабола, координаты вершины параболы, ось симметрии параболы.

Алгебра, 9 класс

Решение задания №11 ОГЭ по математике

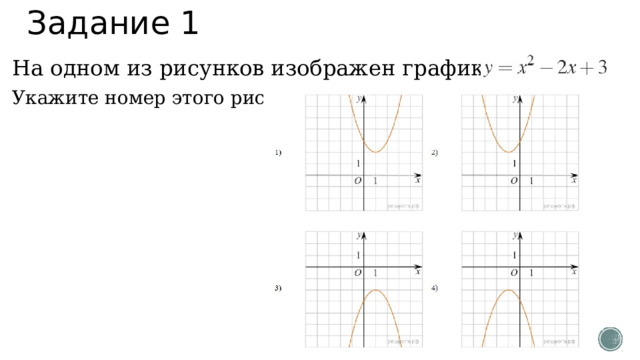
Задание 1

На одном из рисунков изображен график функции

Укажите номер этого рисунка

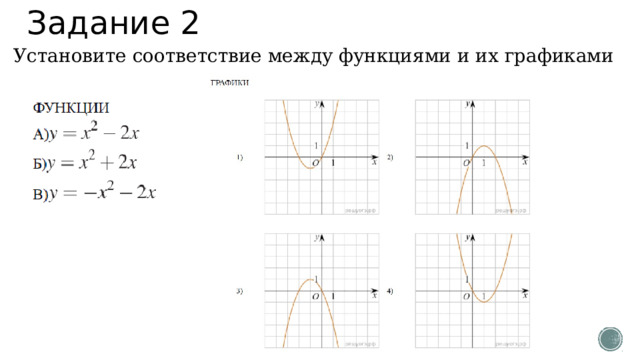
Задание 2

Установите соответствие между функциями и их графиками

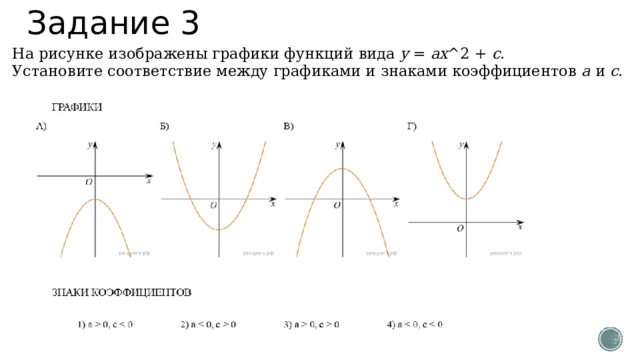
Задание 3

На рисунке изображены графики функций вида y = ax ^2 + c .

Установите соответствие между графиками и знаками коэффициентов a и c .

Задание 4

Установите соответствие между графиками функций и формулами, которые их задают

Решение задания №21 ОГЭ по математике

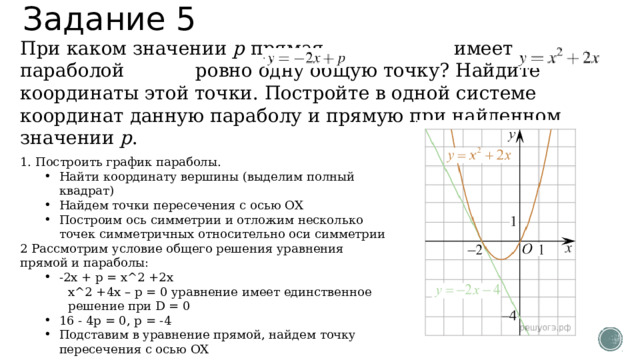
Задание 5

При каком значении p прямая имеет с параболой ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении p .

1. Построить график параболы.

• Найти координату вершины (выделим полный квадрат) Найдем точки пересечения с осью ОХ Построим ось симметрии и отложим несколько точек симметричных относительно оси симметрии
• Найти координату вершины (выделим полный квадрат)
• Найдем точки пересечения с осью ОХ
• Построим ось симметрии и отложим несколько точек симметричных относительно оси симметрии

2 Рассмотрим условие общего решения уравнения прямой и параболы:

• -2х + р = х^2 +2х
• -2х + р = х^2 +2х

x^2 +4x – p = 0 уравнение имеет единственное решение при D = 0

• 16 - 4р = 0, р = -4 Подставим в уравнение прямой, найдем точку пересечения с осью ОХ
• 16 - 4р = 0, р = -4
• Подставим в уравнение прямой, найдем точку пересечения с осью ОХ

Задание 6

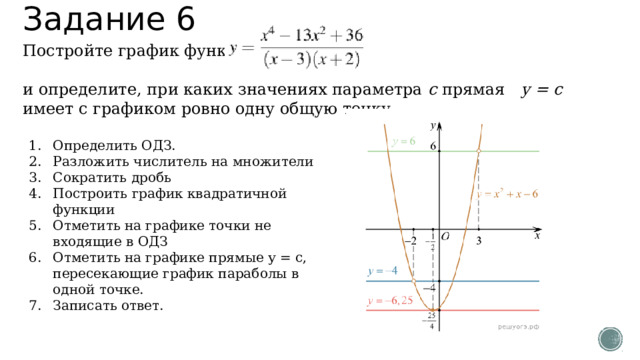
Постройте график функции

и определите, при каких значениях параметра c прямая у = с имеет с графиком ровно одну общую точку.

• Определить ОДЗ.
• Разложить числитель на множители
• Сократить дробь
• Построить график квадратичной функции
• Отметить на графике точки не входящие в ОДЗ
• Отметить на графике прямые у = с, пересекающие график параболы в одной точке.
• Записать ответ.