Презентация по теме" Первый признак равенства треугольников"

ПРЕЗЕНТАЦИЯ К УРОКУ геометрии ПО ТЕМЕ:

«ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ»

Чему ты сегодня должен научиться на уроке:

☻ Понять смысл слов «теорема» и «доказательство теоремы».

☻ Сформулировать и доказать первый признак равенства треугольников.

☻ Учиться решать задачи

• Как ты думаешь, какие два треугольника называются равными?

Определение : два треугольника называются равными, если

1) три угла одного треугольника равны трем углам другого треугольника ,

2) три стороны одного треугольника равны трем

соответственным сторонам другого треугольника. Определение : стороны, которые заключены между равными

углами, называются соответственными.

В

К

М

С

Р

А

∆ АВС = ∆МКР, так как ( по определению)

•  А=  М;  В=  К;  С=  Р;

• АВ = МК; ВС = КР; АС = МР

В

против  А лежит сторона ВС

(напротив  А)

к  А прилежат стороны АВ и АС

(стороны, исходящие из  А)

С

А

Попробуй назвать стороны, лежащие против  В и  С;

стороны, прилежащие к  В и  С.

Проверь себя:

Против ∠В лежит сторона АС, против ∠С лежит сторона АВ.

к  В прилежат стороны АВ и ВС,

к  С прилежат стороны ВС и АС

Теорема - (греч . theorema, от theoreo - рассматриваю) , в математике - предложение (утверждение) , устанавливаемое при помощи цепочки рассуждений. Теорема обычно состоит из условия и заключения.

"если" - это условие (что дано), а после "то" – заключение (что нужно доказать).

Доказательство теоремы - это рассуждения,

с помощью которых устанавливается верность данной теоремы.

Теорема : «Первый признак равенства треугольников»

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Подумай, Что нам дано и Что нужно дока зать.

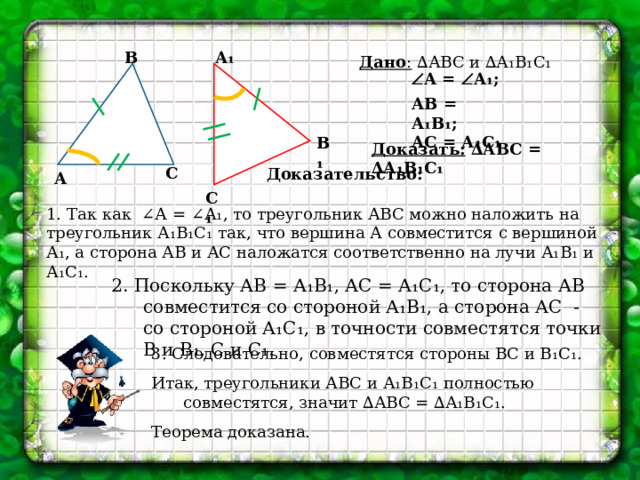
А₁

В

Дано : ∆АВС и ∆А₁В₁С₁

 А =  А₁;

АВ = А₁В₁;

АС = А₁С₁

В₁

Доказать: ∆АВС = ∆А₁В₁С₁

С

Доказательство:

А

С₁

1. Так как ∠А = ∠А₁, то треугольник АВС можно наложить на треугольник А₁В₁С₁ так, что вершина А совместится с вершиной А₁, а сторона АВ и АС наложатся соответственно на лучи А₁В₁ и А₁С₁.

2. Поскольку АВ = А₁В₁, АС = А₁С₁, то сторона АВ совместится со стороной А₁В₁, а сторона АС - со стороной А₁С₁, в точности совместятся точки В и В₁, С и С₁.

3. Следовательно, совместятся стороны ВС и В₁С₁.

Итак, треугольники АВС и А₁В₁С₁ полностью совместятся, значит ∆АВС = ∆А₁В₁С₁.

Теорема доказана.

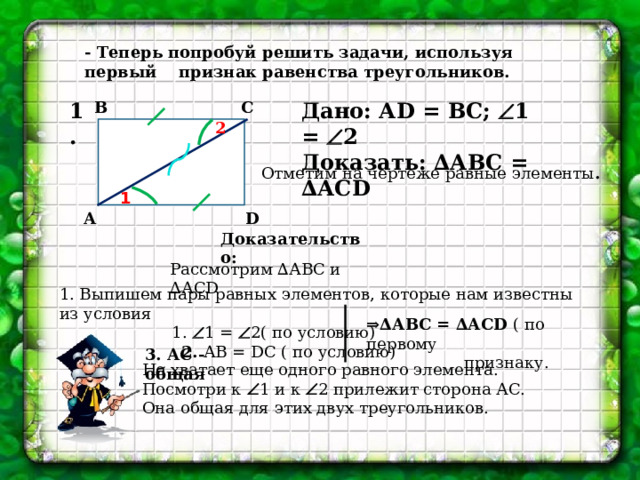
- Теперь попробуй решить задачи, используя первый признак равенства треугольников.

С

Дано: А D = ВС;  1 =  2

Доказать: ∆АВС = ∆АС D

В

1.

2

Отметим на чертеже равные элементы .

1

D

А

Доказательство:

Рассмотрим ∆АВС и ∆АС D

1. Выпишем пары равных элементов, которые нам известны из условия

1.  1 =  2( по условию)

2. АВ = D С ( по условию)

⇒∆ АВС = ∆АС D ( по первому

признаку.

3. АС - общая

Не хватает еще одного равного элемента.

Посмотри к  1 и к  2 прилежит сторона АС.

Она общая для этих двух треугольников.

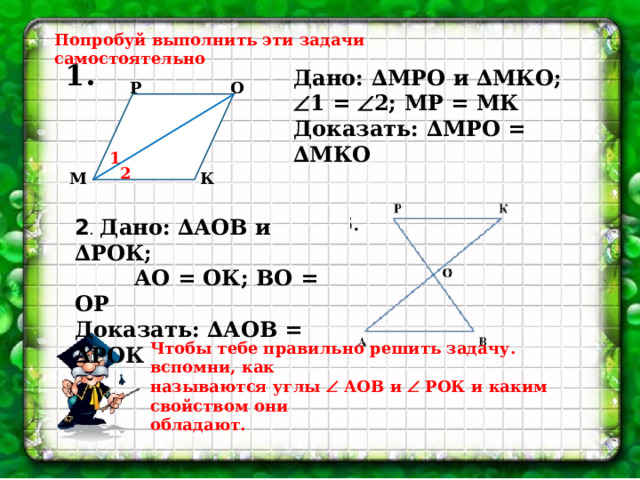
Попробуй выполнить эти задачи самостоятельно

1.

Дано: ∆МРО и ∆МКО;

 1 =  2; МР = МК

Доказать: ∆МРО = ∆МКО

Р

О

1

2

К

М

2 . Дано: ∆АОВ и ∆РОК;

АО = ОК; ВО = ОР

Доказать: ∆АОВ = ∆РОК

Чтобы тебе правильно решить задачу. вспомни, как

называются углы  АОВ и  РОК и каким свойством они

обладают.

• Сформулируй первый признак равенства треугольников.
• Сколько равных элементов нужно найти в треугольниках, чтобы

доказать, что они равны?

Молодец!

Сегодня ты хорошо постарался: познакомился с первым признаком

Равенства треугольников и научился решать задачи, используя данный признак.

Иллюстрации:

• Фон презентации https://multiurok.ru/files/priezientatsiia-po-matiematikie-dlia-3-klassa-na-tiemu-poriadok-vypolnieniia-dieistviia-skobki.html