Презентация по теме "Признак перпендикулярности прямой и плоскости", 10 класс

Признак перпендикулярности прямой и плоскости

10 класс

Перпендикулярность в пространстве

• Обелиск

• Башня

Цель: знать признак перпендикулярности прямой и плоскости

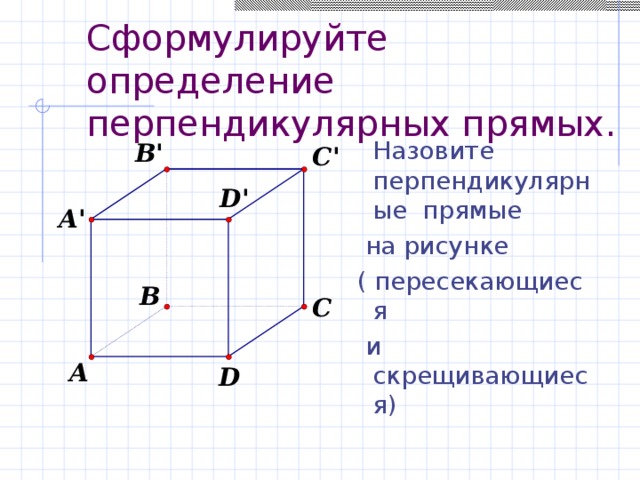
Сформулируйте определение перпендикулярных прямых.

Назовите перпендикулярные прямые

• Назовите перпендикулярные прямые
• Назовите перпендикулярные прямые

на рисунке

( пересекающиеся

и скрещивающиеся)

• на рисунке ( пересекающиеся и скрещивающиеся)
• на рисунке ( пересекающиеся и скрещивающиеся)

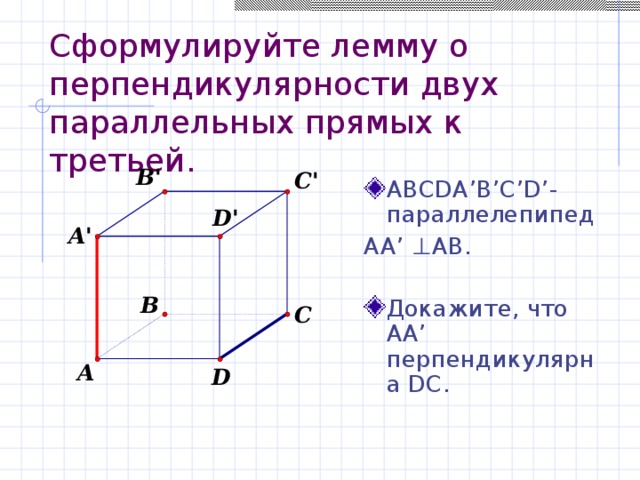
Сформулируйте лемму о перпендикулярности двух параллельных прямых к третьей.

• ABCDA’B’C’D’- параллелепипед

AA’ ⊥AB.

• Докажите, что АА’ перпендикулярна DС.

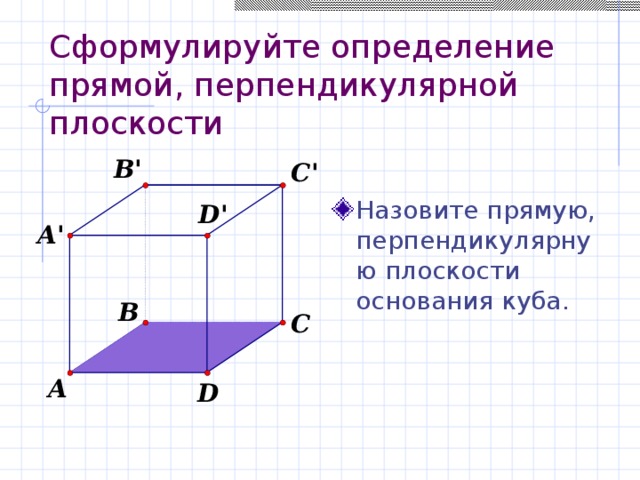
Cформулируйте определение прямой, перпендикулярной плоскости

• Назовите прямую, перпендикулярную плоскости основания куба.

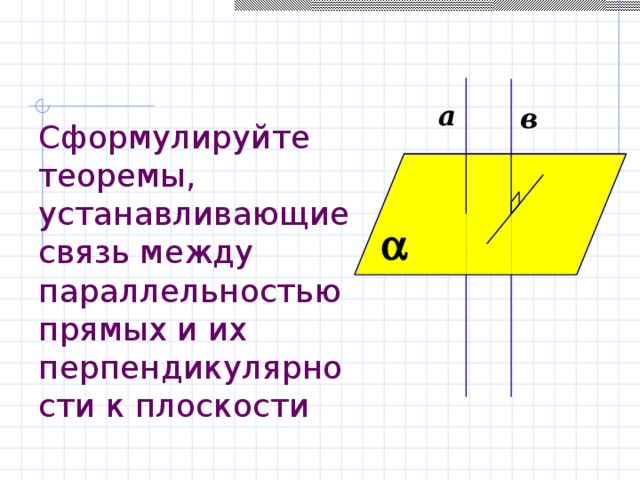
Сформулируйте теоремы, устанавливающие связь между параллельностью прямых и их перпендикулярности к плоскости

Задача №1

• Дано:ABCDA’B’C’D’-куб,

О- точка пересечения AC и BD

F -середина А’С

• Найти: угол между прямыми FO и АВ

Задача №119

• Дано: ОА ⊥ ОВС, О - середина AD,

OB=OC

• Доказать: 1)АВ=DB,

2)AB=AC.

Верны ли утверждения:

Прямая перпендикулярна плоскости, если она перпендикулярна какой–нибудь прямой, лежащей в этой плоскости?

Прямая перпендикулярна плоскости, если она перпендикулярна параллельным прямым?

• Прямая перпендикулярна плоскости, если она перпендикулярна какой–нибудь прямой, лежащей в этой плоскости? Прямая перпендикулярна плоскости, если она перпендикулярна параллельным прямым?

Нет, оба утверждения неверные.

a ⊥b , но а не перпендикулярна α

Признак перпендикулярности прямой и плоскости

• Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.

• Дано: a ⊥p, a⊥q,p⋂q,pє α ,qє α .

• Доказать: а ⊥ α

Первый этап.

Пусть прямая а пересекает плоскость в точке пересечения прямых p и q

• ∆ APQ= ∆ BPQ

( по трем сторонам)

• ∠ APQ = ∠ ВPQ

• ∆ APL= ∆ BPL (по двум сторонам и углу между ними)
• AL=BL

• ∆ ALB -равнобедренный
• OL- медиана и высота
• Ч.т.д.

Второй этап.

• a ‖ a’
• a’ ⊥ α
• a ⊥ α

Проверка перпендикулярности осветительных столбов

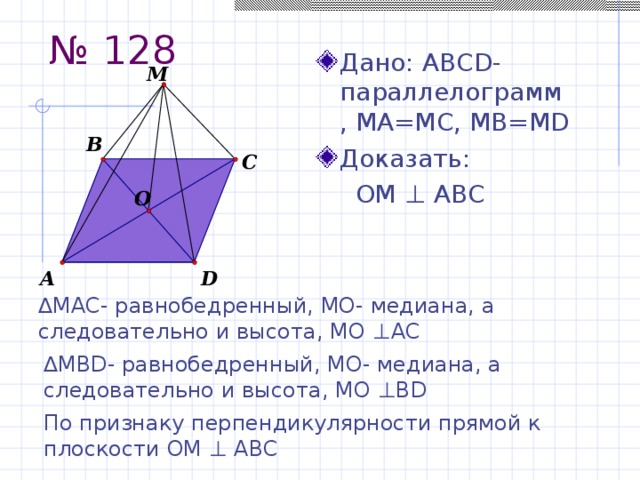
№ 128

• Дано: АBCD-параллелограмм, MA=MC, MB=MD
• Доказать:

ОМ ⊥ АВС

∆ МАС- равнобедренный, МО- медиана, а следовательно и высота, МО ⊥ АС

∆ МBD- равнобедренный, МО- медиана, а следовательно и высота, МО ⊥BD

По признаку перпендикулярности прямой к плоскости ОМ ⊥ АВС

Прямая а проходит через центр круга. Можно ли утверждать, что прямая а перпендикулярна кругу, если

1.она перпендикулярна диаметру

2.двум радиусам

3.двум диаметрам

Проверка вертикальности

Домашнее задание

П .15-17 №124, 126

До новых встреч!