
Вероятность и статистика
7 класс
Пример 1
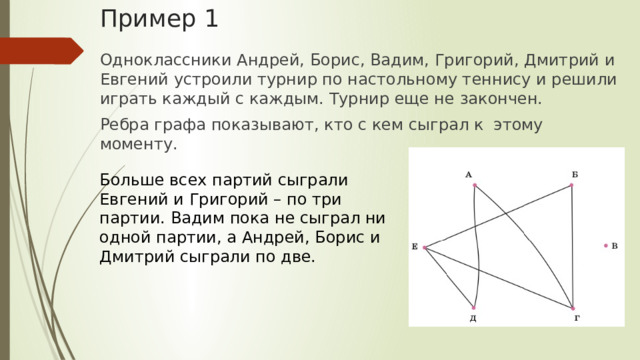
Одноклассники Андрей, Борис, Вадим, Григорий, Дмитрий и Евгений устроили турнир по настольному теннису и решили играть каждый с каждым. Турнир еще не закончен.
Ребра графа показывают, кто с кем сыграл к этому моменту.
Больше всех партий сыграли Евгений и Григорий – по три партии. Вадим пока не сыграл ни одной партии, а Андрей, Борис и Дмитрий сыграли по две.

Степень (валентность) вершины. Число рёбер и суммарная степень вершин.
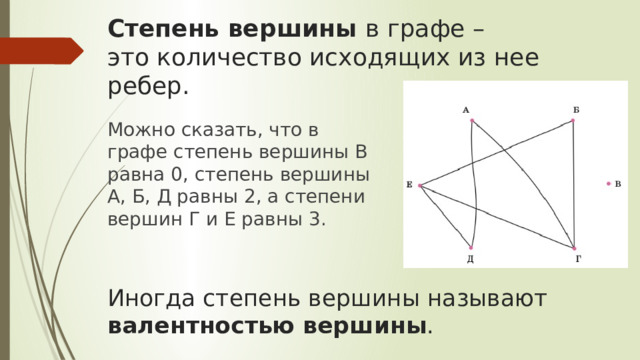
Степень вершины в графе – это количество исходящих из нее ребер.
Можно сказать, что в графе степень вершины В равна 0, степень вершины А, Б, Д равны 2, а степени вершин Г и Е равны 3.
Иногда степень вершины называют валентностью вершины .
Граф с петлей
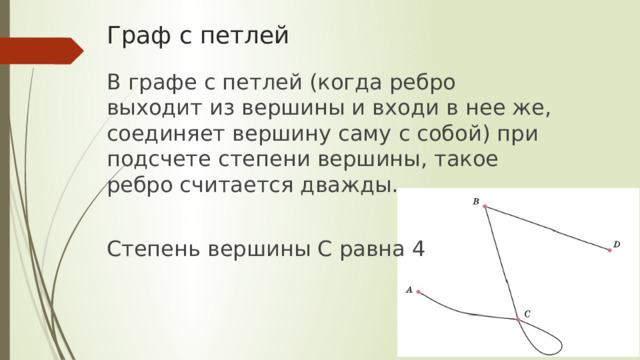
В графе с петлей (когда ребро выходит из вершины и входи в нее же, соединяет вершину саму с собой) при подсчете степени вершины, такое ребро считается дважды.
Степень вершины С равна 4

Пример 2
На рисунке два графа. В них по 4 вершины и по 3 ребра.
Можно ли считать их одинаковыми?
Нет.
У них разное количество степеней.
У каждого ребра два конца, поэтому сумма степеней всех вершин в два раза больше числа ребер, то есть четное число.

Пример 3 (Задача о рукопожатиях)
Во время встречи некоторые участники пожали руки другим. Докажите, что количество участников, сделавших нечетное число рукопожатий четно.
Решение: Представим себе граф рукопожатий: каждого участника обозначим вершиной, а тех, кто пожал друг другу руки соединим ребром.
Пускай во встрече участвовало n человек, которые пожали руки другим четное число раз, и k человек, которые сделали нечетное число рукопожатий. Тогда в графе оказывается ровно n вершин четной степени и k вершин нечетной степени.
Пример 3
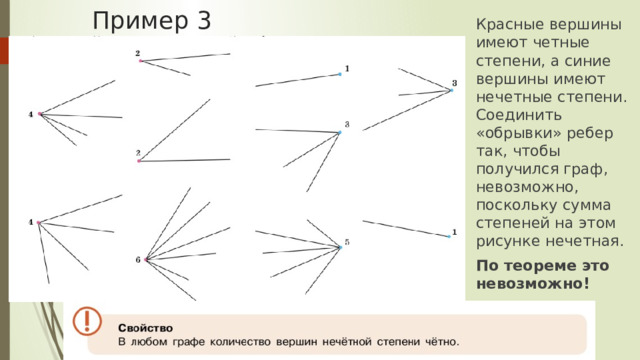
Красные вершины имеют четные степени, а синие вершины имеют нечетные степени. Соединить «обрывки» ребер так, чтобы получился граф, невозможно, поскольку сумма степеней на этом рисунке нечетная.
По теореме это невозможно!

Закрепление
- Придумайте и нарисуйте два неодинаковых графа, в каждом из которых 6 вершин со степенями 1,1,2,2,3,3
- На конференцию собрались ученые. Могло ли оказаться так, что пятеро из них знакомы ровно с тремя другими, а все остальные имеют ровно четверых знакомых среди собравшихся?
- Придумайте и нарисуйте 3 неодинаковых графа, в каждом из которых по 6 ребер. Найдите сумму степеней всех вершин каждого из этих графов.

Домашнее задание






































