Презентация «Полуправильные многогранники»

БПОУ ВО «Воронежский государственный промышленно-гуманитарный колледж им. В.М. Пескова»

Полуправильные многогранники (справочные материалы)

Разработчик: Н.Л.Латышева

«Многогранники – фигуры особого очарования с богатой родословной» Клауди Альсина, испанский математик, профессор.

Призма

Антипризма

Пирамида

Параллелепипед

Усеченная пирамида

Тела Кеплера-Пуансо

Тела Архимеда

Тела Платона

Каталановы тела

Соединения многогранников

Другие звездчатые многогранники

Тела Архимеда

Архимед обобщил понятие правильного многогранника и открыл новые математические объекты – полуправильные многогранники . Так он назвал многогранники, у которых все грани – правильные многоугольники более, чем одного рода, а все многогранные углы конгруэнтны(эквивалентны).

Только в наше время удалось доказать, что тринадцатью открытыми Архимедом полуправильными многогранниками исчерпывается все множество этих геометрических фигур.

АРХИМЕД  (287 - 212 до н.э.) - древнегреческий математик, физик и механик.

Родился в Сиракузах. Предполагают, что его отцом был астроном Фидий.

В Архимеде гениально сочетались качества ученого и инженера. Он основоположник статики и гидростатики.

Архимед - автор многочисленных открытий и изобретений:

• машины для орошения полей,
• водоподъемного механизма (архимедов винт),
• системы рычагов, блоков для подъема больших тяжестей,
• военных метательных машин и т.п.

Во время 2-й Пунической войны он возглавил оборону Сиракуз. Его метательные машины вынудили римлян отказаться от попытки взять город штурмом и заставили перейти к осаде. В трудный час для отчизны Архимед поставил все свои знания на службу согражданам и погиб, защищая отечество от неприятеля.

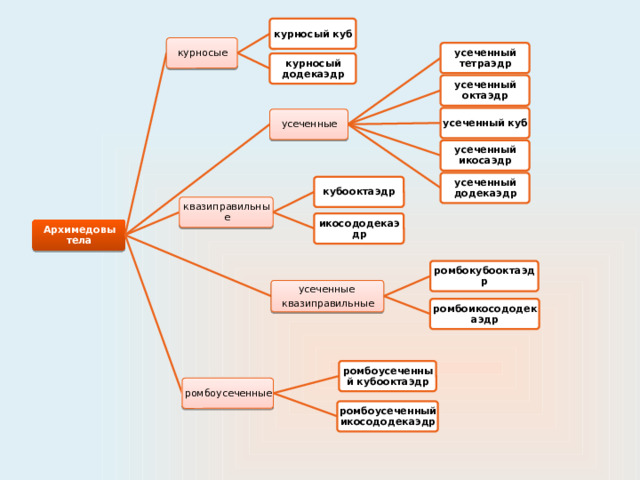
курносый куб

курносые

усеченный тетраэдр

курносый додекаэдр

усеченный октаэдр

усеченный куб

усеченные

усеченный икосаэдр

усеченный додекаэдр

кубооктаэдр

квазиправильные

икосододекаэдр

Архимедовы тела

ромбокубооктаэдр

усеченные

квазиправильные

ромбоикосододекаэдр

ромбоусеченный кубооктаэдр

ромбоусеченные

ромбоусеченный икосододекаэдр

Усечённый тетраэдр

Многогранник получается при последовательном срезании каждой из вершин тетраэдра.

Усечённый тетраэдр - полуправильный выпуклый многогранник, обладающий двумя свойствами:

• Все грани являются правильными многоугольниками двух типов – 4 правильных шестиугольника и 4 правильных треугольника;
• Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую.

Количество граней: 8  Количество ребер: 18  Количество вершин: 12

Граней при вершине: 3

Усечённый октаэдр

Многогранник получается при последовательном срезании каждой из вершин октаэдра.

Усечённый октаэдр - полуправильный выпуклый многогранник, обладающий двумя свойствами:

1. Все грани являются правильными многоугольниками двух типов – 8 шестиугольников и 6 четырехугольников;

2. Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую.

Количество граней: 14  Количество ребер: 36  Количество вершин: 24

Граней при вершине: 3

Единственное архимедово тело, при повторении которого можно заполнить все пространство целиком.

Усечённый икосаэдр

Многогранник получается при последовательном срезании каждой из вершин икосаэдра.

Усечённый икосаэдр - полуправильный выпуклый многогранник, обладающий двумя свойствами:

1. Все грани являются правильными многоугольниками двух типов – 20 шестиугольников и 12 пятиугольников;

2. Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую.

Количество граней: 32 Количество ребер: 90 Количество вершин: 60

Граней при вершине: 3

Главной особенностью этого многогранника является то, что его форма послужила основой для  изготовления футбольного мяча. Это становится очевидным, после того как применить черно-белый вариант окраски граней.

Усечённый гексаэдр (куб)

Многогранник получается при последовательном срезании каждой из вершин гексаэдра.

Усечённый гексаэдр - полуправильный выпуклый многогранник, обладающий двумя свойствами:

• Все грани являются правильными многоугольниками двух типов – 6 восьмиугольников и 8 треугольников;
• 2. Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую.

Количество граней: 14 Количество ребер: 36  Количество вершин: 24

Граней при вершине: 3

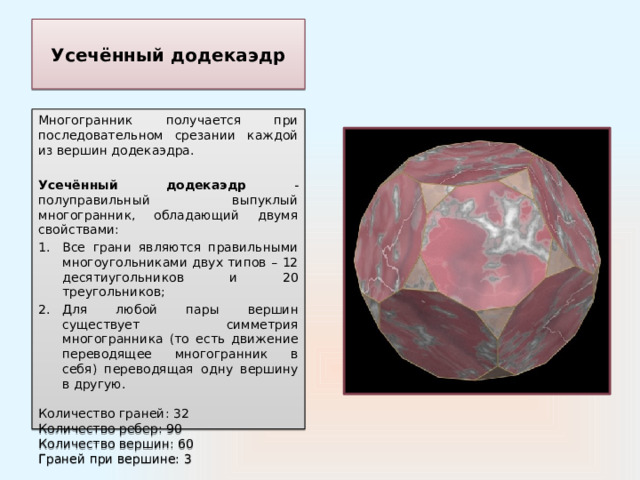
Усечённый додекаэдр

Многогранник получается при последовательном срезании каждой из вершин додекаэдра.

Усечённый додекаэдр - полуправильный выпуклый многогранник, обладающий двумя свойствами:

• Все грани являются правильными многоугольниками двух типов – 12 десятиугольников и 20 треугольников;
• Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую.

Количество граней: 32  Количество ребер: 90 Количество вершин: 60

Граней при вершине: 3

Кубо-октаэдр

Многогранник получается при последовательном срезании каждой из вершин октаэдра.

Кубо-октаэдр - полуправильный выпуклый многогранник, обладающий двумя свойствами: 1. Все грани являются правильными многоугольниками двух типов – 8 треугольников и 6 квадратов;

2. Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую.

Граней - 14

Вершин - 12

Ребер - 24

Граней при вершине - 4

Икосо-додекаэдр

Многогранник получается при последовательном срезании каждой из вершин додекаэдра.

Икосо-додекаэдр  - полуправильный выпуклый многогранник, обладающий двумя свойствами: 1. Все грани являются правильными многоугольниками двух типов – 12 пятиугольников и 20 треугольников;

2. Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую.

Граней - 32

Вершин - 30  

Ребер - 60

Граней при вершине - 4

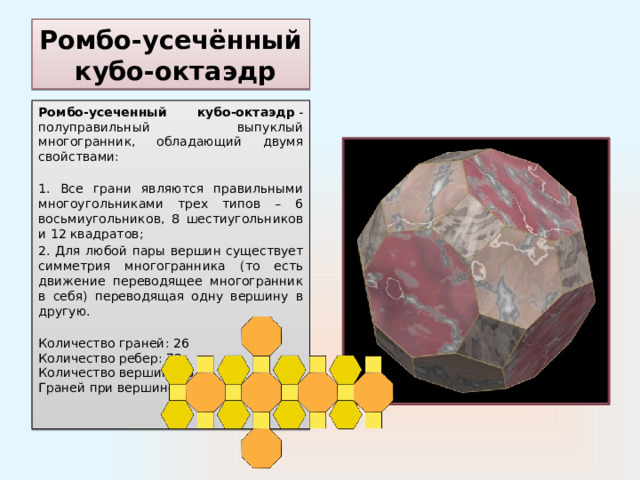
Ромбо-усечённый кубо-октаэдр

Ромбо-усеченный кубо-октаэдр  - полуправильный выпуклый многогранник, обладающий двумя свойствами:

1. Все грани являются правильными многоугольниками трех типов – 6 восьмиугольников, 8 шестиугольников и 12 квадратов;

2. Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую.

Количество граней: 26  Количество ребер: 72  Количество вершин: 48

Граней при вершине: 3

Ромбо-усечённый икосо-додекаэдр

Ромбо - усечённый икосо - додекаэдр - полуправильный выпуклый многогранник, обладающий двумя свойствами:

1. Все грани являются правильными многоугольниками трех типов – 12 десятиугольников, 20 шестиугольников и 30 квадратов;

2. Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую.

Количество граней: 62 Количество ребер: 180 Количество вершин: 120

Граней при вершине: 3

Ромбо-кубо-октаэдр

Многогранник получается при последовательном срезании каждой из вершин октаэдра.

Ромбо-кубо-октаэдр  - полуправильный выпуклый многогранник, обладающий двумя свойствами:

1. Все грани являются правильными многоугольниками двух типов – 8 треугольников и 18 квадратов;

2. Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую.

Количество граней: 26 Количество ребер: 48 Количество вершин: 24

Граней при вершине: 4

Ромбо – икосо –додекаэдр

Многогранник получается при последовательном срезании каждой из вершин икосо-додекаэдра..

Ромбо – икосо – додекаэдр  - полуправильный выпуклый многогранник, обладающий двумя свойствами:

1. Все грани являются правильными многоугольниками трёх типов – 12 пятиугольников, 30 четырехугольников и 20 треугольников;

2. Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую.

Количество граней: 62  Количество ребер: 120 Количество вершин: 60

Граней при вершине: 4

Курносый куб

Плосконосый (курносый) куб  - полуправильный выпуклый многогранник, обладающий двумя свойствами:

• Все грани являются правильными многоугольниками двух типов – 32 треугольника и 6 квадратов;
• Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую.

Количество граней: 38 Количество ребер: 60 Количество вершин: 24

Граней при вершине: 5

Курносый куб можно получить последовательным срезанием каждой из вершин гексаэдра. Он может быть изготовлен в одном из двух вариантов - имеющий  закрутку влево  и имеющий  закрутку вправо .

При определении метрических свойств курносого куба приходится решать кубические уравнения и пользоваться кубическими корнями. Поэтому курносый куб, в отличие от Платоновых и большинства архимедовых тел, не допускает построения с помощью только циркуля и линейки. То же верно и для курносого додекаэдра.

Курносый додекаэдр

Плосконосый (курносый) додекаэдр  - полуправильный выпуклый многогранник, обладающий двумя свойствами:

• Плосконосый (курносый) додекаэдр имеет 92 грани (наибольшее количество из всех архимедовых тел), 12 из них являются пятиугольниками, а остальные 80 —правильными треугольниками;
• Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую.

Курносый додекаэдр получается последовательным срезанием каждой из вершин додекаэдра. Многогранник может быть изготовлен в одном из двух вариантов - имеющий  закрутку влево  и имеющий  закрутку вправо .

Количество граней: 92  Количество ребер: 150 Количество вершин: 160

Граней при вершине: 5

Двойственность полуправильных многогранников

В то время как многогранники, двойственные пяти правильным многогранникам, принадлежат к тому же семейству, архимедовы тела порождают 13 совершенно новых многогранников . До конца 19 в. никто не уделял внимание этим объектам.

Каталановы Тела

Двойственные архимедовым телам, так называемые  Каталановы тела , имеют конгруэнтные грани (переводимые друг в друга сдвигом, вращением или отражением), равные двугранные углы и правильные многогранные углы.

Каталановы тела тоже иногда называют полуправильными многогранниками. Архимедовы тела являются полуправильными многогранниками в том смысле, что их грани — правильные многоугольники, но они не одинаковы, а Каталановы — в том смысле, что их грани одинаковы, но не являются правильными многоугольниками.

Каталан Эжен Шарль (1814 - 1894) - бельгийский математик, член Бельгийской АН (с 1865). 

Родился в Брюгге. Окончил Политехническую школу в Париже. Преподавал там же и в Сорбонне.

В 1849 отказался присягнуть Наполеону III и был лишен права преподавания.

В 1865 году Каталан получил кафедру анализа в Льежском университете и сделан членом Брюссельской академии. Правительство Бельгии наградило его рыцарским крестом ордена Леопольда в 1879 году.

Член-корреспондент Петербургской АН (с 1881).

Основные работы относятся к геометрии, работал также в области математического анализа и механики. Каталан написал более 200 мемуаров, ставящих его в число лучших геометров 19 века.

Кроме Каталановых тел, его именем назван так же важный класс чисел, использующихся во множестве задач комбинаторики.

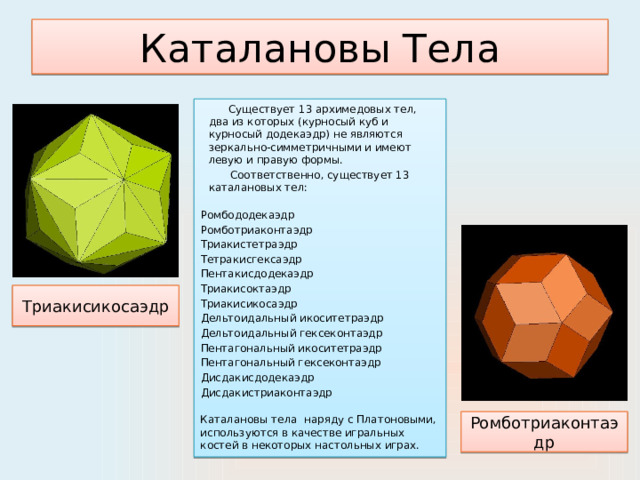
Каталановы Тела

Существует 13 архимедовых тел, два из которых (курносый куб и курносый додекаэдр) не являются зеркально-симметричными и имеют левую и правую формы.

Соответственно, существует 13 каталановых тел:

Ромбододекаэдр 

Ромботриаконтаэдр 

Триакистетраэдр 

Тетракисгексаэдр

Пентакисдодекаэдр 

Триакисоктаэдр 

Триакисикосаэдр 

Дельтоидальный икоситетраэдр

Дельтоидальный гексеконтаэдр

Пентагональный икоситетраэдр 

Пентагональный гексеконтаэдр 

Дисдакисдодекаэдр

Дисдакистриаконтаэдр

Каталановы тела наряду с Платоновыми, используются в качестве игральных костей в некоторых настольных играх.

Триакисикосаэдр

Ромботриаконтаэдр

Ромбододекаэдр

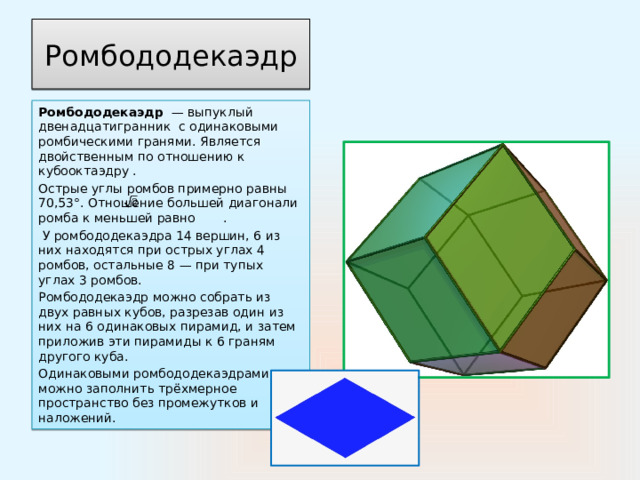
Ромбододекаэдр   — выпуклый двенадцатигранник  с одинаковыми ромбическими гранями. Является двойственным по отношению к кубооктаэдру .

Острые углы ромбов примерно равны 70,53°. Отношение большей диагонали ромба к меньшей равно  .

У ромбододекаэдра 14 вершин, 6 из них находятся при острых углах 4 ромбов, остальные 8 — при тупых углах 3 ромбов.

Ромбододекаэдр можно собрать из двух равных кубов, разрезав один из них на 6 одинаковых пирамид, и затем приложив эти пирамиды к 6 граням другого куба.

Одинаковыми ромбододекаэдрами можно заполнить трёхмерное пространство без промежутков и наложений. 

Ромботриаконтаэдр

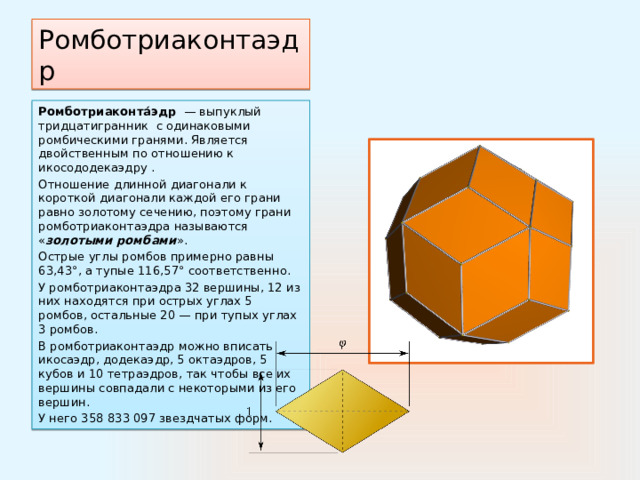
Ромботриаконтáэдр   — выпуклый тридцатигранник  с одинаковыми ромбическими гранями. Является двойственным по отношению к икосододекаэдру .

Отношение длинной диагонали к короткой диагонали каждой его грани равно золотому сечению, поэтому грани ромботриаконтаэдра называются « золотыми ромбами ».

Острые углы ромбов примерно равны 63,43°, а тупые 116,57° соответственно.

У ромботриаконтаэдра 32 вершины, 12 из них находятся при острых углах 5 ромбов, остальные 20 — при тупых углах 3 ромбов.

В ромботриаконтаэдр можно вписать икосаэдр, додекаэдр, 5 октаэдров, 5 кубов и 10 тетраэдров, так чтобы все их вершины совпадали с некоторыми из его вершин.

У него 358 833 097 звездчатых форм.

Триакистетраэдр

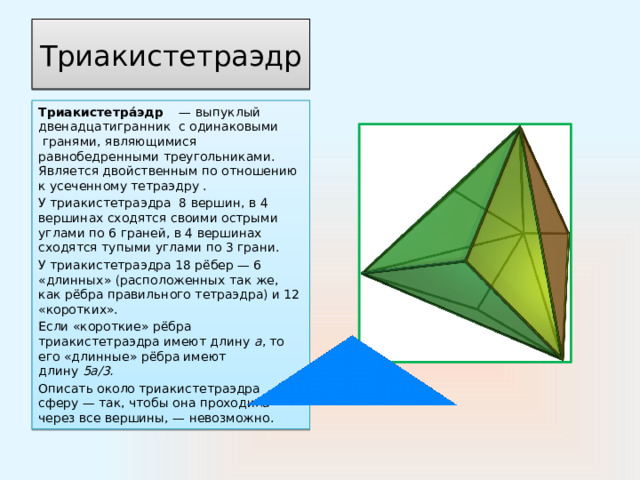
Триакистетра́эдр     — выпуклый двенадцатигранник  с одинаковыми  гранями, являющимися равнобедренными треугольниками. Является двойственным по отношению к усеченному тетраэдру .

У триакистетраэдра  8 вершин, в 4 вершинах сходятся своими острыми углами по 6 граней, в 4 вершинах сходятся тупыми углами по 3 грани.

У триакистетраэдра 18 рёбер — 6 «длинных» (расположенных так же, как рёбра правильного тетраэдра) и 12 «коротких».

Если «короткие» рёбра триакистетраэдра имеют длину  a , то его «длинные» рёбра имеют длину  5а/3.

Описать около триакистетраэдра сферу — так, чтобы она проходила через все вершины, — невозможно.

Тетракисгексаэдр

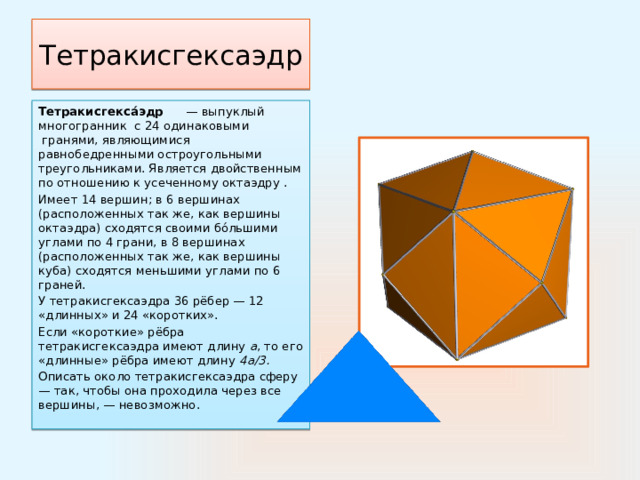
Тетракисгекса́эдр       — выпуклый многогранник  с 24 одинаковыми  гранями, являющимися равнобедренными остроугольными треугольниками. Является двойственным по отношению к усеченному октаэдру .

Имеет 14 вершин; в 6 вершинах (расположенных так же, как вершины октаэдра) сходятся своими бо́льшими углами по 4 грани, в 8 вершинах (расположенных так же, как вершины куба) сходятся меньшими углами по 6 граней.

У тетракисгексаэдра 36 рёбер — 12 «длинных» и 24 «коротких».

Если «короткие» рёбра тетракисгексаэдра имеют длину  a , то его «длинные» рёбра имеют длину  4а/3.

Описать около тетракисгексаэдра сферу — так, чтобы она проходила через все вершины, — невозможно.

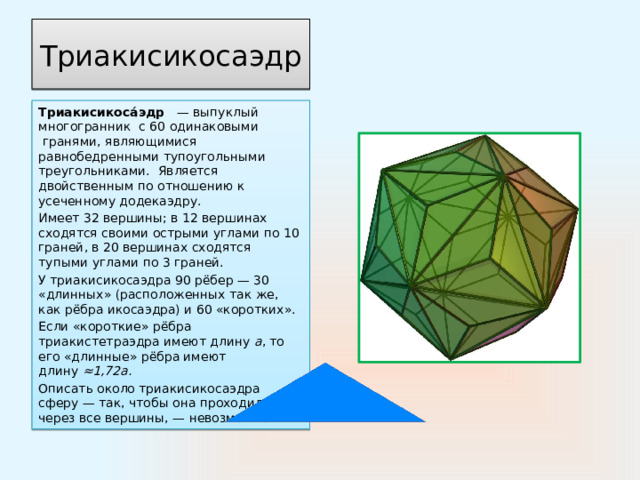
Триакисикосаэдр

Триакисикоса́эдр   — выпуклый многогранник  с 60 одинаковыми  гранями, являющимися равнобедренными тупоугольными треугольниками. Является двойственным по отношению к усеченному додекаэдру.

Имеет 32 вершины; в 12 вершинах сходятся своими острыми углами по 10 граней, в 20 вершинах сходятся тупыми углами по 3 граней.

У триакисикосаэдра 90 рёбер — 30 «длинных» (расположенных так же, как рёбра икосаэдра) и 60 «коротких». 

Если «короткие» рёбра триакистетраэдра имеют длину  a , то его «длинные» рёбра имеют длину  ≈1,72а.

Описать около триакисикосаэдра  сферу — так, чтобы она проходила через все вершины, — невозможно.

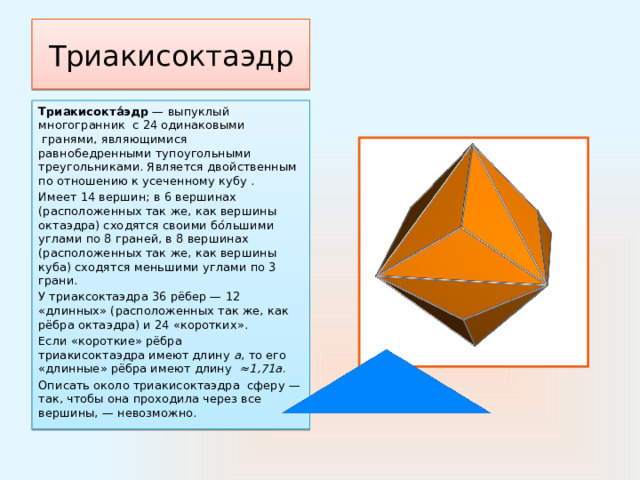
Триакисоктаэдр

Триакисокта́эдр  — выпуклый многогранник  с 24 одинаковыми  гранями, являющимися равнобедренными тупоугольными треугольниками. Является двойственным по отношению к усеченному кубу .

Имеет 14 вершин; в 6 вершинах (расположенных так же, как вершины октаэдра) сходятся своими бо́льшими углами по 8 граней, в 8 вершинах (расположенных так же, как вершины куба) сходятся меньшими углами по 3 грани.

У триаксоктаэдра 36 рёбер — 12 «длинных» (расположенных так же, как рёбра октаэдра) и 24 «коротких».

Если «короткие» рёбра триакисоктаэдра имеют длину  a , то его «длинные» рёбра имеют длину  ≈1,71а.

Описать около триакисоктаэдра  сферу — так, чтобы она проходила через все вершины, — невозможно.

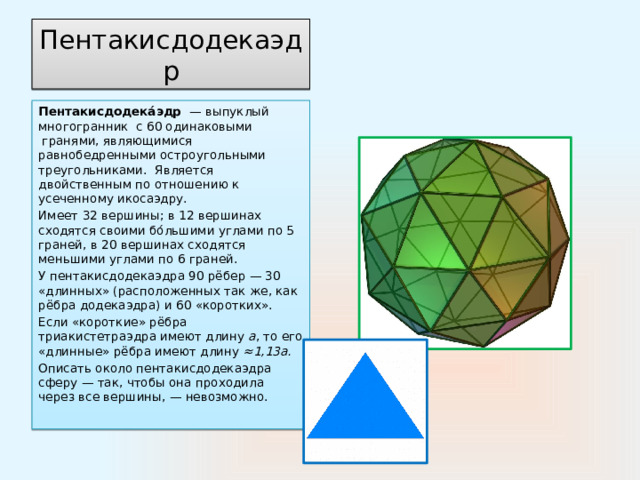
Пентакисдодекаэдр

Пентакисдодека́эдр   — выпуклый многогранник  с 60 одинаковыми  гранями, являющимися равнобедренными остроугольными треугольниками. Является двойственным по отношению к усеченному икосаэдру.

Имеет 32 вершины; в 12 вершинах сходятся своими бо́льшими углами по 5 граней, в 20 вершинах сходятся меньшими углами по 6 граней.

У пентакисдодекаэдра 90 рёбер — 30 «длинных» (расположенных так же, как рёбра додекаэдра) и 60 «коротких». 

Если «короткие» рёбра триакистетраэдра имеют длину  a , то его «длинные» рёбра имеют длину  ≈1,13а.

Описать около пентакисдодекаэдра сферу — так, чтобы она проходила через все вершины, — невозможно.

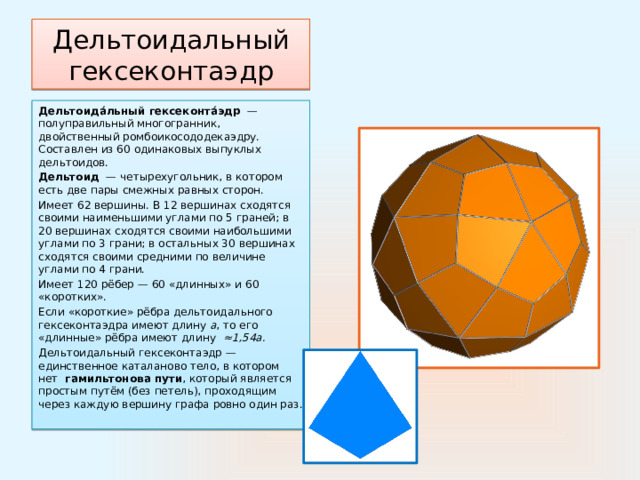
Дельтоидальный гексеконтаэдр

Дельтоида́льный гексеконта́эдр   —полуправильный многогранник, двойственный ромбоикосододекаэдру. Составлен из 60 одинаковых выпуклых дельтоидов.

Дельтоид   — четырехугольник, в котором есть две пары смежных равных сторон.

Имеет 62 вершины. В 12 вершинах сходятся своими наименьшими углами по 5 граней; в 20 вершинах сходятся своими наибольшими углами по 3 грани; в остальных 30 вершинах сходятся своими средними по величине углами по 4 грани.

Имеет 120 рёбер — 60 «длинных» и 60 «коротких».

Если «короткие» рёбра дельтоидального гексеконтаэдра имеют длину  a , то его «длинные» рёбра имеют длину  ≈1,54а.

Дельтоидальный гексеконтаэдр — единственное каталаново тело, в котором нет  гамильтонова пути , который является простым путём (без петель), проходящим через каждую вершину графа ровно один раз.

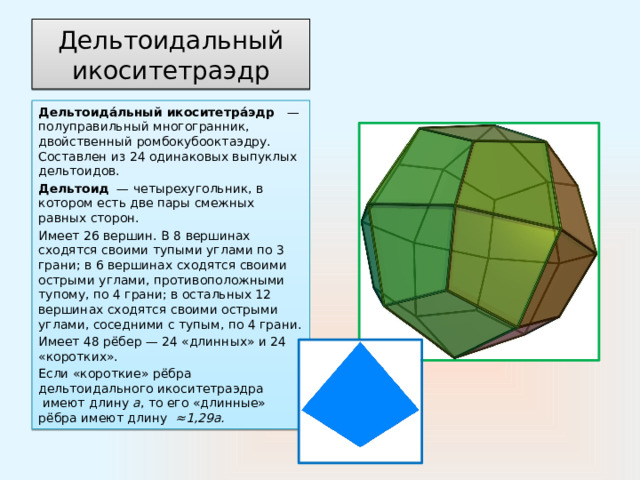
Дельтоидальный икоситетраэдр

Дельтоида́льный икоситетра́эдр   —полуправильный многогранник, двойственный ромбокубооктаэдру. Составлен из 24 одинаковых выпуклых дельтоидов.

Дельтоид   — четырехугольник, в котором есть две пары смежных равных сторон.

Имеет 26 вершин. В 8 вершинах сходятся своими тупыми углами по 3 грани; в 6 вершинах сходятся своими острыми углами, противоположными тупому, по 4 грани; в остальных 12 вершинах сходятся своими острыми углами, соседними с тупым, по 4 грани.

Имеет 48 рёбер — 24 «длинных» и 24 «коротких».

Если «короткие» рёбра дельтоидального икоситетраэдра  имеют длину  a , то его «длинные» рёбра имеют длину  ≈1,29а.

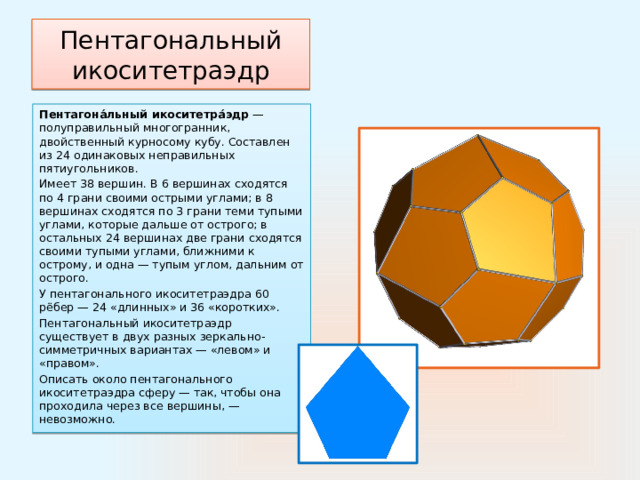
Пентагональный икоситетраэдр

Пентагона́льный икоситетра́эдр  —полуправильный многогранник, двойственный курносому кубу. Составлен из 24 одинаковых неправильных пятиугольников.

Имеет 38 вершин. В 6 вершинах сходятся по 4 грани своими острыми углами; в 8 вершинах сходятся по 3 грани теми тупыми углами, которые дальше от острого; в остальных 24 вершинах две грани сходятся своими тупыми углами, ближними к острому, и одна — тупым углом, дальним от острого.

У пентагонального икоситетраэдра 60 рёбер — 24 «длинных» и 36 «коротких».

Пентагональный икоситетраэдр существует в двух разных зеркально-симметричных вариантах — «левом» и «правом».

Описать около пентагонального икоситетраэдра сферу — так, чтобы она проходила через все вершины, — невозможно.

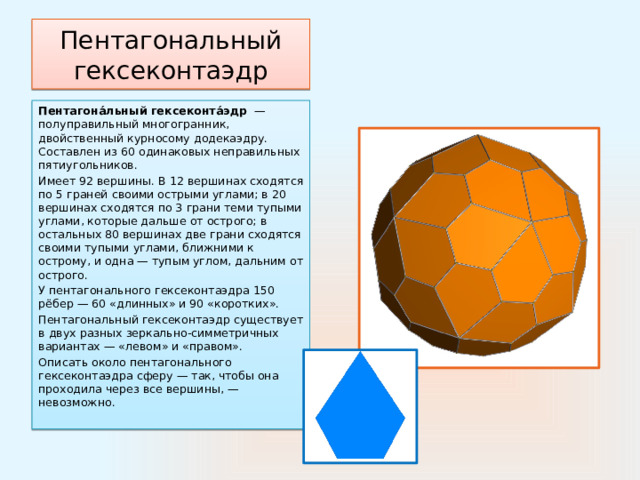
Пентагональный гексеконтаэдр

Пентагона́льный гексеконта́эдр  —полуправильный многогранник, двойственный курносому додекаэдру. Составлен из 60 одинаковых неправильных пятиугольников.

Имеет 92 вершины. В 12 вершинах сходятся по 5 граней своими острыми углами; в 20 вершинах сходятся по 3 грани теми тупыми углами, которые дальше от острого; в остальных 80 вершинах две грани сходятся своими тупыми углами, ближними к острому, и одна — тупым углом, дальним от острого.

У пентагонального гексеконтаэдра 150 рёбер — 60 «длинных» и 90 «коротких».

Пентагональный гексеконтаэдр существует в двух разных зеркально-симметричных вариантах — «левом» и «правом».

Описать около пентагонального гексеконтаэдра сферу — так, чтобы она проходила через все вершины, — невозможно.

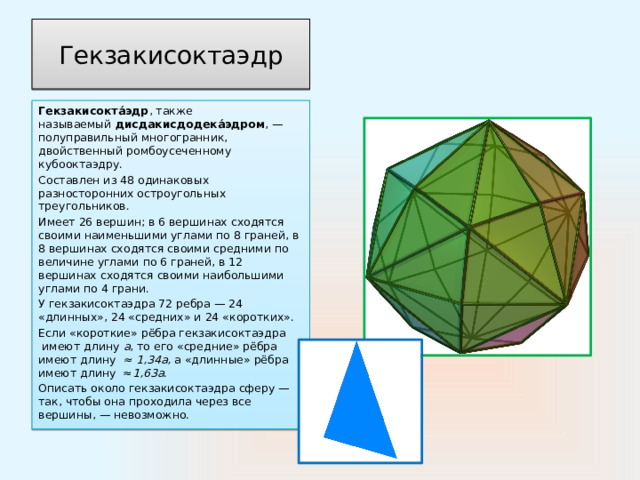
Гекзакисоктаэдр

Гекзакисокта́эдр , также называемый  дисдакисдодека́эдром , —полуправильный многогранник, двойственный ромбоусеченному кубооктаэдру.

Составлен из 48 одинаковых разносторонних остроугольных треугольников.

Имеет 26 вершин; в 6 вершинах сходятся своими наименьшими углами по 8 граней, в 8 вершинах сходятся своими средними по величине углами по 6 граней, в 12 вершинах сходятся своими наибольшими углами по 4 грани.

У гекзакисоктаэдра 72 ребра — 24 «длинных», 24 «средних» и 24 «коротких».

Если «короткие» рёбра гекзакисоктаэдра  имеют длину  a , то его «средние» рёбра имеют длину  ≈ 1,34а, а «длинные» рёбра имеют длину  ≈ 1,63а.

Описать около гекзакисоктаэдра сферу — так, чтобы она проходила через все вершины, — невозможно.

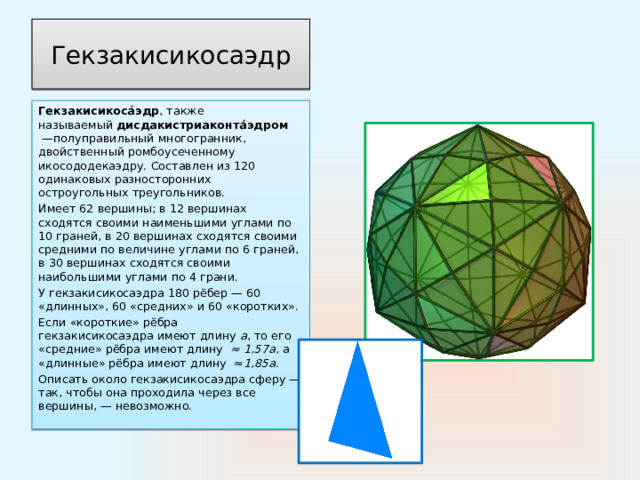
Гекзакисикосаэдр

Гекзакисикоса́эдр , также называемый  дисдакистриаконта́эдром   —полуправильный многогранник, двойственный ромбоусеченному икосододекаэдру. Составлен из 120 одинаковых разносторонних остроугольных треугольников.

Имеет 62 вершины; в 12 вершинах сходятся своими наименьшими углами по 10 граней, в 20 вершинах сходятся своими средними по величине углами по 6 граней, в 30 вершинах сходятся своими наибольшими углами по 4 грани.

У гекзакисикосаэдра 180 рёбер — 60 «длинных», 60 «средних» и 60 «коротких». 

Если «короткие» рёбра гекзакисикосаэдра имеют длину  a , то его «средние» рёбра имеют длину  ≈ 1,57а, а «длинные» рёбра имеют длину  ≈ 1,85а.

Описать около гекзакисикосаэдра сферу — так, чтобы она проходила через все вершины, — невозможно.

Свойства архимедовых и каталановых тел

Архимедовы тела

Каталановы тела

• грани – правильные многоугольники 2-х или 3-х видов
• в вершинах сходится одинаковое число ребер
• для каждого архимедова тела существует описанная сфера, проходящая через все его вершины

• грани – не правильные многоугольники одного вида
• в вершинах сходится разное число ребер
• для каждого каталанова тела существует вписанная сфера, касающаяся всех его граней

«Почему мы не рассматриваем многогранники сами по себе, не наслаждаемся их красотой и удивительными свойствами?» Марждори Сенешаль, американский математик, профессор.

Источники: Мир математики: в 40 т. Т. 23: Клауди Альсина. Тысяча граней геометрической красоты. Многогранники. / Пер. с исп. – М.: Де Агостини, 2014. – 144 с. http://mnogogranniki.ru http://www.geometry2006.narod.ru/Lecture/SemRegPol/SemRegPol.htm http://geometry-and-art.ru/index.html https://tetraksis.com/glavnaya/polygon/polygon2 http://www.wikiwand.com/ru http://school-37.ru/downloads/poly/uniform/index.htm https://www.calc.ru/geom.html http://mathworld.wolfram.com/topics/ArchimedeanSolids.html