Презентация "Построение графиков кусочных функций"

Обобщающий интегрированный урок в 9 классе, рассчитан на 2 академических часа

Учитель:

Тарусова Ольга Тимофеевна

МБОУ СОШ№4

с углубленным изучением отдельных предметов

город Батайск

201 3

Организация продуктивной деятельности обучающихся, направленной на достижение ими следующих результатов:

Метапредметных:

В познава тельной деятельности :

• уметь разделять процессы на этапы, шаги; помочь учащимся осознать социальную, практическую и личную значимость учебного материала; умение планировать и осуществлять деятельность, направленную на решение исследовательских задач творческое решение учебных и практических задач: умение мотивированно отказываться от образца, искать оригинальные решения; самостоятельное выполнение различных творческих работ;
• уметь разделять процессы на этапы, шаги;
• помочь учащимся осознать социальную, практическую и личную значимость учебного материала;
• умение планировать и осуществлять деятельность, направленную на решение исследовательских задач
• творческое решение учебных и практических задач: умение мотивированно отказываться от образца, искать оригинальные решения;
• самостоятельное выполнение различных творческих работ;

в информационно –коммуникативной деятельности :

• умение вступать в речевое общение, участвовать в диалоге (понимать точку зрения собеседника, признавать право на иное мнение); умение формулировать вопросы, задачи; умение перефразировать вопросы, задачи умение отражать в устной или письменной форме результаты своей деятельности
• умение вступать в речевое общение, участвовать в диалоге (понимать точку зрения собеседника, признавать право на иное мнение);
• умение формулировать вопросы, задачи;
• умение перефразировать вопросы, задачи
• умение отражать в устной или письменной форме результаты своей деятельности

в рефлексивной деятельности :

• самостоятельно организовать учебную деятельность (постановка цели, планирование, определение оптимального соотношения цели и средств); осуществлять поиск и устранять причины возникших трудностей в ходе решения задач; овладеть умением совместной деятельности, направленным на сотрудничество; объективное оценивание своей деятельности на уроке
• самостоятельно организовать учебную деятельность (постановка цели, планирование, определение оптимального соотношения цели и средств);
• осуществлять поиск и устранять причины возникших трудностей в ходе решения задач;
• овладеть умением совместной деятельности, направленным на сотрудничество;
• объективное оценивание своей деятельности на уроке

предметные :

• понимание алгоритма построения графиков кусочных функций, заданных формулой; Овладение навыками чтения графиков кусочных функций; Понимание сути основных свойств графиков кусочных функций Овладение опытом творческой деятельности при решении заданий связанных кусочными функциями
• понимание алгоритма построения графиков кусочных функций, заданных формулой;
• Овладение навыками чтения графиков кусочных функций;
• Понимание сути основных свойств графиков кусочных функций
• Овладение опытом творческой деятельности при решении заданий связанных кусочными функциями

личностные :

• Получать удовольствие от уроков математики; Умение выражать свои мысли в устной и письменной форме; Уверенно и легко выполнять построение и чтение графиков функций; Овладеть умением применять полученные знания в нестандартных ситуациях Умение вступать в речевое общение, участвовать в диалоге; Формирование характера и личности.
• Получать удовольствие от уроков математики;
• Умение выражать свои мысли в устной и письменной форме;
• Уверенно и легко выполнять построение и чтение графиков функций;
• Овладеть умением применять полученные знания в нестандартных ситуациях
• Умение вступать в речевое общение, участвовать в диалоге;
• Формирование характера и личности.

• Организационный момент
• Проверка домашнего задания‹
• Устная актуализация знаний
• Тест по проверке знаний основных этапов построения графиков
• Работа с индивидуальными заданиями в парах
• Физкультминутка
• Расширение представлений о кусочных функциях
• Вывод по результатам деятельности. Обобщение полученных выводов
• Подведение итогов урока
• Домашнее задании

1) Алгоритм построения графиков функций у=| f ( x )| покажем на примере построения графика функции y=|x 2 -2x-3|

Построение:

Чтобы построить график данной функции нужно

- построить параболу y=x 2 -2x-3

- часть графика над ОХ сохранить, а часть графика расположенную ниже ОХ отобразить симметрично относительно оси ОХ

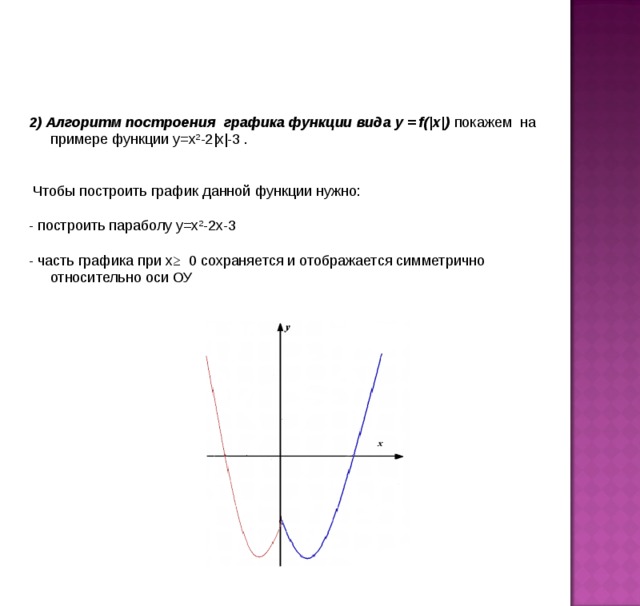
2) Алгоритм построения графика функции вида y = f(|x|) покажем на примере функции y=x 2 -2|x|-3 .

Чтобы построить график данной функции нужно:

- построить параболу y=x 2 -2x-3

- часть графика при х≥ 0 сохраняется и отображается симметрично относительно оси ОУ

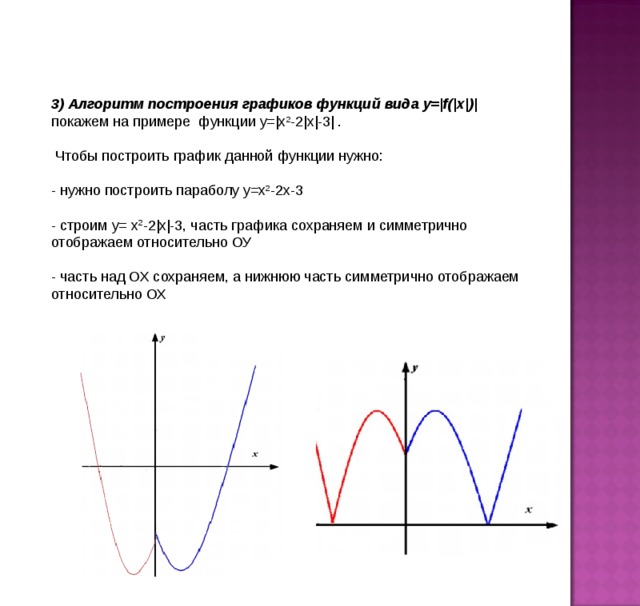
3) Алгоритм построения графиков функций вида y=|f(|x|)| покажем на примере функции y=|x 2 -2|x|-3| .

Чтобы построить график данной функции нужно:

- нужно построить параболу у=x 2 -2x-3

- строим у= x 2 -2|x|-3, часть графика сохраняем и симметрично отображаем относительно ОУ

- часть над ОХ сохраняем, а нижнюю часть симметрично отображаем относительно ОХ

Найдите соответствие между функциями и графиками, объясните ваш выбор

8

7

у = Rx+b

У=х 3

у=х 2

у=х -2 n

у = R/x

у =∛ x

у=| x|

у =√ x

1. Какая линия является графиком функции у = - (х-3) 2  +2?

А. прямая, проходящая через начало координат

Б. парабола

В. прямая, не проходящая через начало координат

Г. гипербола

2. График функции у=2(х+2) 2  получится из графика функции у=2х 2  сдвигом на 2 единицы масштаба

А. вправо

Б. влево

В. вверх

Г. вниз

3. Какая из функций является ограниченной сверху

А. у=2х 2

Б. у=-3 (х-2) 2 +3

В. у=3х 2 -1

Г. у=х+3

4. Для функции у=2(х-2) 2 +3 вспомогательные оси имеют уравнения вида:

А. х=2; у=3.

Б. х=-2; у=3.

В. х=2; у=-3

Г. х=-2; у=-3

1 вариант

а) Построить график кусочной функции

б) Найдите: f (-5); f (-3); f (5).

2 вариант

а)Построить график кусочной функции

б ) Найдите: f (-6); f (-3); f (8).

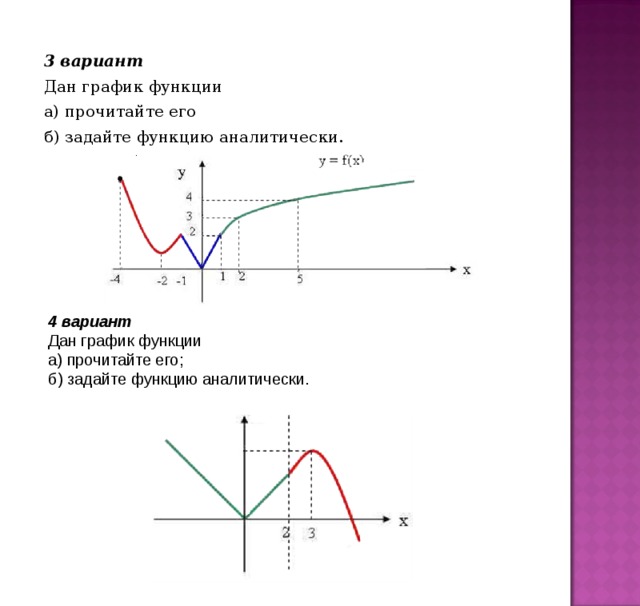
3 вариант

Дан график функции

а) прочитайте его

б) задайте функцию аналитически.

4 вариант

Дан график функции

а) прочитайте его;

б) задайте функцию аналитически.

4. б) Чтобы найти f (-5) надо найти промежуток которому принадлежит число-5 это х≤-4. На этом промежутке построен график функции f ( X )=3, значит f (-5)=3. Число -3 принадлежит промежутку -4‹х ≤4, f (-3)=│(-3) 2 -4│-3│+3│=0. Число 5 из промежутка x 4, f (5)=3-(5-4) 2 =2 " width="640"

1 вариант

а) Рассмотрим отдельно каждую функцию и построим её график. Так, f ( X )=3-прямая параллельная оси Ох, но изображать её нужно только на участке, где х≤-4. График функции f (х)=| x 2 -4| x |+3| может быть получен из параболы у= x 2 -4 x +3. Построив её график, часть рисунка, которая лежит над осью Ох, необходимо оставить без изменения, а часть, которая лежит под осью абсцисс, симметрично отобразить относительно оси Ox. Затем симметрично отобразить часть графика ,где x ≥ 0 относительно оси Oy для отрицательных x. Полученный в результате всех преобразований график оставляем только на участке от -4‹х ≤4

График третьей функции – парабола, ветви которой направлены вниз, а вершина находится в точке с координатами (4; 3). Чертеж изображаем только на участке, где x 4.

б) Чтобы найти f (-5) надо найти промежуток которому принадлежит число-5 это

х≤-4. На этом промежутке построен график функции f ( X )=3, значит f (-5)=3. Число -3 принадлежит промежутку -4‹х ≤4, f (-3)=│(-3) 2 -4│-3│+3│=0. Число 5 из промежутка

x 4, f (5)=3-(5-4) 2 =2

2 вариант

а)Графиком первой функции является парабола у=-х 2 , вершина которой находится в точке с координатой (-6;8). Чертёж изображаем только на участке х‹6. График функции f (х)=| x 2 -6| x |+8| может быть получен из параболы у= x 2 -6 x +8. Построив её график, часть рисунка, которая лежит над осью Ох, необходимо оставить без изменения, а часть, которая лежит под осью абсцисс, симметрично отобразить относительно оси Ox. Затем симметрично отобразить часть графика ,где x ≥ 0 относительно оси Oy для отрицательных x. Полученный в результате всех преобразований график оставляем только на участке от -6 ≤ х ‹5.График третьей функции прямая параллельная оси Ох, но изображать её нужно только на участке, где х≥5.

б) Чтобы найти f (-6) надо найти промежуток которому принадлежит число -6 это

-6 ≤ х ‹5. На этом промежутке построен график функции f ( X )=| x 2 -6| x |+8| , поэтому

f (-6)=8. Число -3 также принадлежит промежутку -6 ≤ х ‹5

f (-3)=│(-3) 2 -6│-3│+8│=1. Число 8 из промежутка х≥5, поэтому f (8)=3.

3 вариант

а)

б) На отрезке построена парабола у=х 2 сдвинутая по оси ох на 2 единичных отрезка влево и на 1 единичный отрезок вверх по осио у, поэтому функция записывается так у=(х+2) 2 +1. На отрезке по оси ох на 1 единичный отрезок враво и на 2 единичных отрезка по оси оу вверх , поэтому функция записывается так у=

4 вариант

Для снятия утомляемости глаз

Нельзя водить руками, а лишь только глазами. В таблице расположены числа от 1 до 20, но 4 числа пропущены, ваша задача назвать эти числа.

5

13

19

18

12

1

4

3

8

14

9

16

20

10

15

6

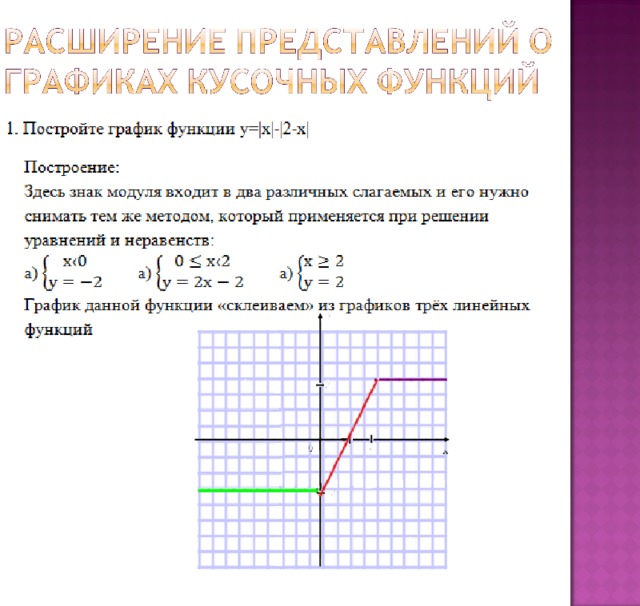
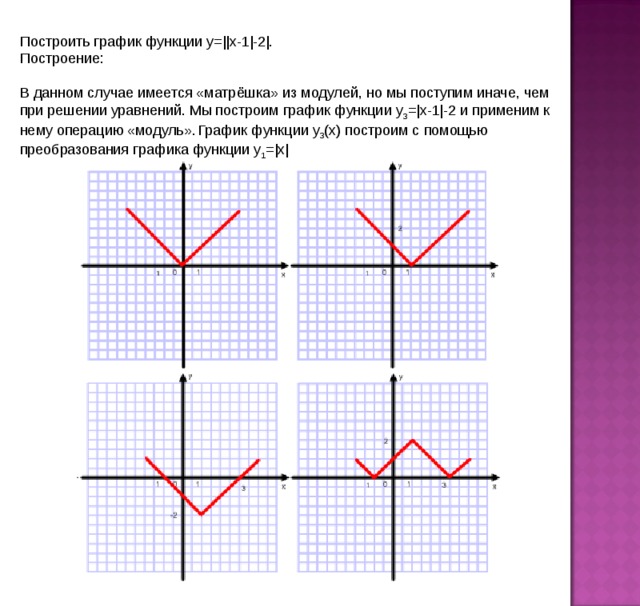
Построить график функции у=|| x -1|-2|.

Построение:

В данном случае имеется «матрёшка» из модулей, но мы поступим иначе, чем при решении уравнений. Мы построим график функции у 3 =| x -1|-2 и применим к нему операцию «модуль». График функции у 3 (х) построим с помощью преобразования графика функции у 1 =| x |

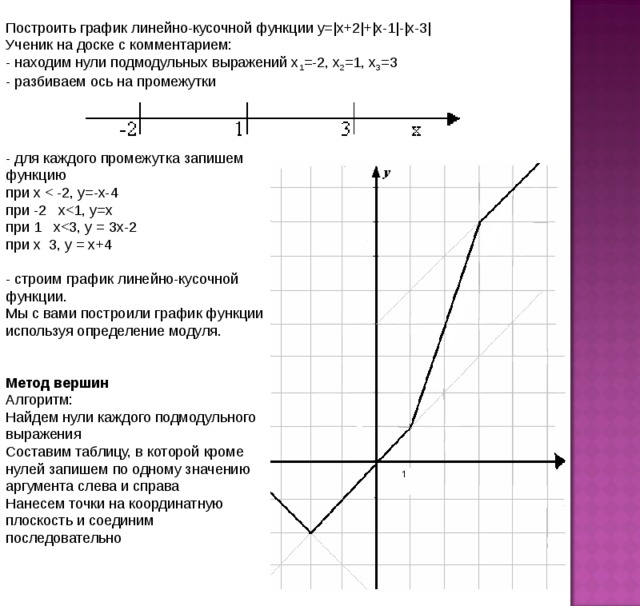
Построить график линейно-кусочной функции у=|х+2|+|х-1|-|х-3|

Ученик на доске с комментарием:

- находим нули подмодульных выражений х 1 =-2, х 2 =1, х 3 =3

- разбиваем ось на промежутки

- для каждого промежутка запишем функцию

при х

при -2   х

при 1   х

при х  3, у = х+4

- строим график линейно-кусочной функции.

Мы с вами построили график функции используя определение модуля.

Метод вершин

Алгоритм:

Найдем нули каждого подмодульного выражения

Составим таблицу, в которой кроме нулей запишем по одному значению аргумента слева и справа

Нанесем точки на координатную плоскость и соединим последовательно

Что мы должны уметь :

• Уметь строить график степенной функции.
• Умеем строить график функции содержащей модуль
• Уметь по графику составлять формулы функции.
• Уметь строить и читать кусочные функции.

Чтобы построить график кусочной функции, нужно :

• Построить в одной системе координат графики входящих функций;
• Провести прямые  x=a 1 , x=a 2 , ..., x=a n , где  a i  - граничные точки;
• На каждой составляющей области определения ( a i ;  a i+1 ), где  i =1.. n  выбрать тот график, который соответствует входящей функции на этой составляющей;
• Выяснить значение функции в граничных точках.

Предлагаю вам подумать каких целей вы достигли в результате работы на уроке и что не удалось.

Цели:

• Узнать для себя что-то новое
• Получить хорошую отметку
• Показать свою эрудицию
• Узнать о практическом применении в жизни графиков кусочных функций
• Научить логически мыслить , рассуждать и говорить

Спасибо за урок!

1. Функции — это математические портреты устойчивых закономерностей, познаваемых человеком. Чтобы проиллюстрировать характерные свойства функций, мне показалось естественным обратиться к пословицам. Ведь пословицы — это тоже отражение устойчивых закономерностей, выверенное многовековым опытом народа, поэтому попробуйте найти функциональные зависимости в следующих пословицах, нарисовать эскизы графиков и назвать характерные свойства этих графиков.

1 «Выше меры конь не скачет»

2. «Пересев хуже недосева»

3.«Чем дальше в лес, тем больше дров»

4. «Каши маслом не испортишь»

• «Горяч на почине, да скоро остыл»

Какая из эти функциональных зависимостей имеет максимум, какая ограничена и снизу и сверху, какая монотонно возрастает, какая монотонно убывает а какая имеет вогнутость

2. Построить график функции:

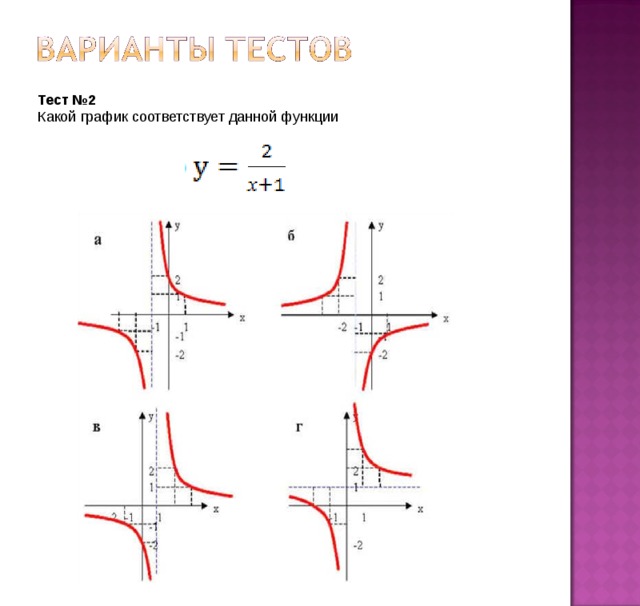
Тест №2

Какой график соответствует данной функции

у = │ х - 2│ + 2

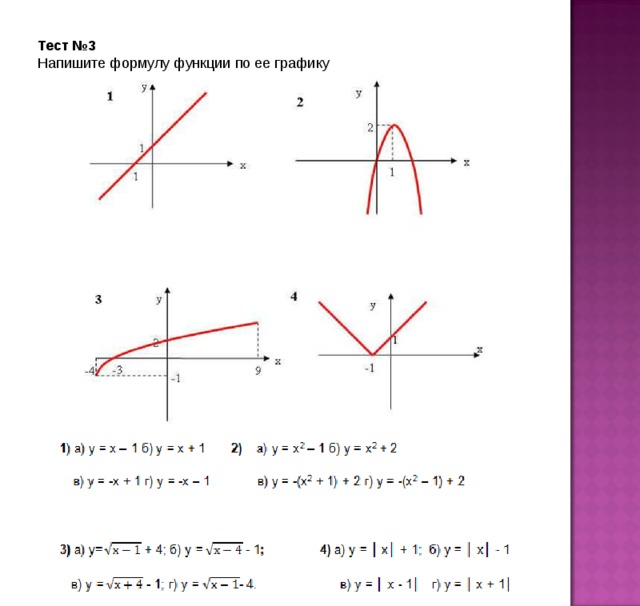
Тест №3

Напишите формулу функции по ее графику

Проверка домашнего задания

• «Выше меры конь не скачет» Если представить траекторию скачущего коня как график некоторой функции, то высота скачков в полном соответствии с пословицей будет ограничена сверху некоторой «мерой». Это будет знакомый график функции синуса.
• «Пересев хуже недосева» Урожай лишь до некоторой поры растет вместе с плотностью посева, дальше он снижается, потому что при чрезмерной густоте ростки начинают глушить друг друга. Эта закономерность станет особенно наглядной, если изобразить ее графиком, где урожай представлен как функция плотности посева. Урожай максимален, когда поле засеяно в меру. Максимум— это наибольшее значение функции по сравнению с ее значениями во всех соседних точках. Это как бы вершина горы, с которой все дороги ведут только вниз, куда ни шагни.
• «Чем дальше в лес, тем больше дров» Можно изобразить графиком, как нарастает количество дров по мере продвижения в глубь леса – от опушки, где все давным-давно собрано, до чащоб, куда не ступала нога заготовителя. График представляет количество дров как функцию пути. Согласно пословице эта функция неизменно возрастает. Такое свойство функции называется монотонным возрастанием.
• «Каши маслом не испортишь» Качество каши можно рассматривать как функцию количества масла в ней. Согласно пословице эта функция не уменьшается с добавкой масла. Она, возможно, увеличивается, но может оставаться и на прежнем уровне. Подобного рода функция называется монотонно неубывающей.
• «Горяч на почине, да скоро остыл»Обе функции, зависящие от времени, возрастающие. Но, как видно, расти можно по-разному. Наклон одной кривой постоянно увеличивается. Рост функции усиливается с ростом аргумента. Такое свойство функции называется вогнутостью.

П

О

С

Л

О

В

И

Ц

Ы