Презентация "Примеры решения задач на смеси и сплавы"

• Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

• Имеется два сплава. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

• Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

• Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

• В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

• Смешали 4 литра 15–процентного водного раствора некоторого вещества с 6 литрами 25–процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

• Смешали некоторое количество 15–процентного раствора некоторого вещества с таким же количеством 19–процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

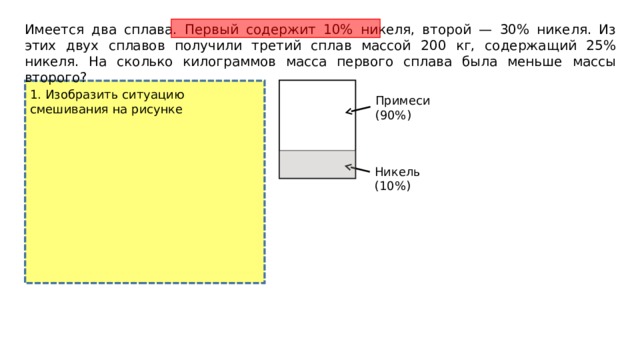
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

1. Изобразить ситуацию смешивания на рисунке

Примеси (90%)

Никель (10%)

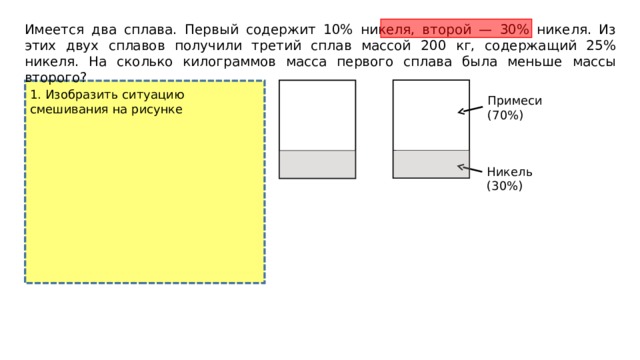
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

1. Изобразить ситуацию смешивания на рисунке

Примеси (70%)

Никель (30%)

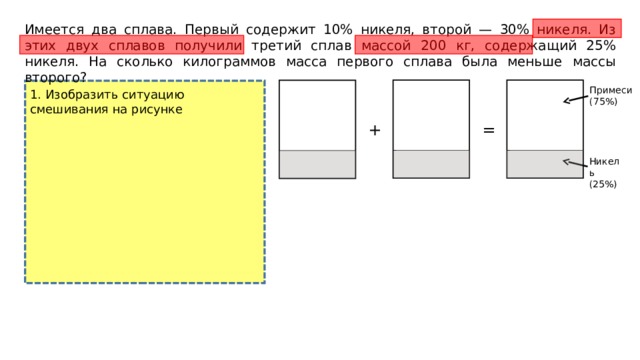
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

Примеси (75%)

1. Изобразить ситуацию смешивания на рисунке

=

+

Никель (25%)

Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

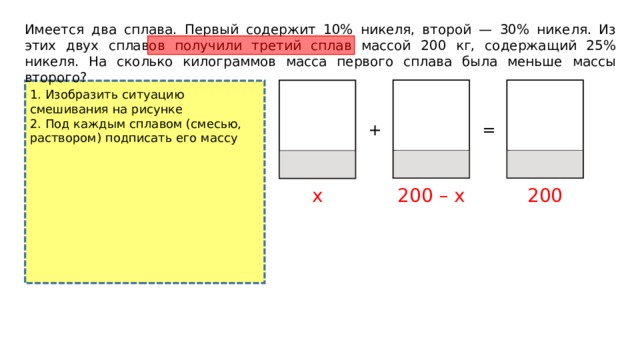
1. Изобразить ситуацию смешивания на рисунке

2. Под каждым сплавом (смесью, раствором) подписать его массу

=

+

200

200 – x

x

Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым сплавом (смесью, раствором) подписать его массу

3. Подписать массу чистого вещества в каждом сплаве (смеси, растворе)

М(чистого в-ва) = Конц ∙ М(сплава)

+

=

0,1x

0,3(200-x)

0,25 ∙ 200

200

200 – x

x

Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым сплавом (смесью, раствором) подписать его массу

3. Подписать массу чистого вещества в каждом сплаве (смеси, растворе)

М(чистого в-ва) = Конц ∙ М(сплава)

4. Составить и решить уравнение

+

=

Никель

Никель

Никель

0,3(200-x)

0,25 ∙ 200

0,1x

200

200 – x

x

0,1х + 0,3(200 – x) = 0,25 ∙ 200

0,1x + 60 – 0,3x = 50

0,1x – 0,3x = 50 – 60

-0,2x = -10

x = -10 : (-0,2)

x = 50

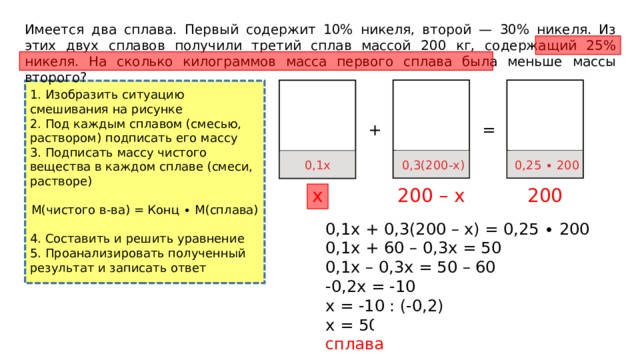
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым сплавом (смесью, раствором) подписать его массу

3. Подписать массу чистого вещества в каждом сплаве (смеси, растворе)

М(чистого в-ва) = Конц ∙ М(сплава)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

+

=

0,3(200-x)

0,25 ∙ 200

0,1x

200 – x

200

x

0,1х + 0,3(200 – x) = 0,25 ∙ 200

0,1x + 60 – 0,3x = 50

0,1x – 0,3x = 50 – 60

-0,2x = -10

x = -10 : (-0,2)

x = 50 (кг) – масса первого сплава

150 – 50 = 100

Ответ: 100

Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым сплавом (смесью, раствором) подписать его массу

3. Подписать массу чистого вещества в каждом сплаве (смеси, растворе)

М(чистого в-ва) = Конц ∙ М(сплава)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

=

+

0,25 ∙ 200

0,3(200-x)

0,1x

200 – x

200

x

0,1х + 0,3(200 – x) = 0,25 ∙ 200

0,1x + 60 – 0,3x = 50

0,1x – 0,3x = 50 – 60

-0,2x = -10

x = -10 : (-0,2)

x = 50 (кг) – масса первого сплава

200 – 50 = 150 (кг) – масса 2-го сплава

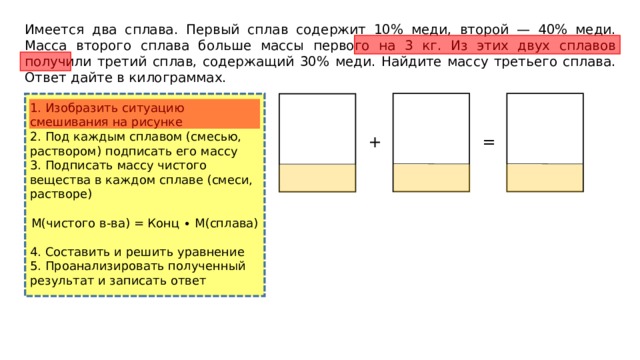
Имеется два сплава. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым сплавом (смесью, раствором) подписать его массу

3. Подписать массу чистого вещества в каждом сплаве (смеси, растворе)

М(чистого в-ва) = Конц ∙ М(сплава)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

+

=

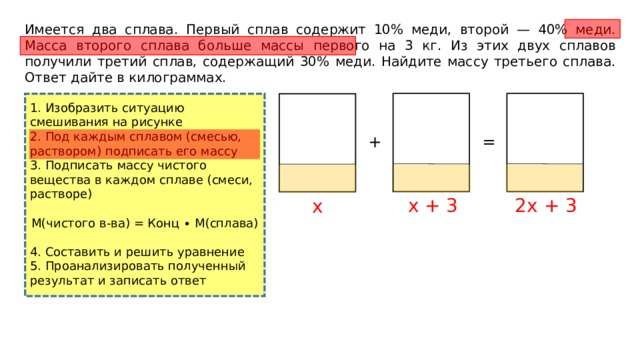
Имеется два сплава. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым сплавом (смесью, раствором) подписать его массу

3. Подписать массу чистого вещества в каждом сплаве (смеси, растворе)

М(чистого в-ва) = Конц ∙ М(сплава)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

+

=

2x + 3

x + 3

x

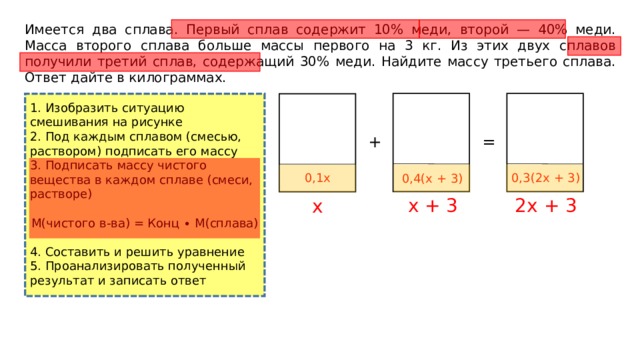
Имеется два сплава. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым сплавом (смесью, раствором) подписать его массу

3. Подписать массу чистого вещества в каждом сплаве (смеси, растворе)

М(чистого в-ва) = Конц ∙ М(сплава)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

+

=

0,3(2x + 3)

0,1x

0,4(x + 3)

x + 3

2x + 3

x

Имеется два сплава. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым сплавом (смесью, раствором) подписать его массу

3. Подписать массу чистого вещества в каждом сплаве (смеси, растворе)

М(чистого в-ва) = Конц ∙ М(сплава)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

+

=

Медь

Медь

Медь

0,3(2x + 3)

0,1x

0,4(x + 3)

2x + 3

x + 3

x

0,1х + 0,4(x + 3) = 0,3(2x + 3)

0,1x + 0,4x + 1,2 = 0,6x + 0,9

0,1x + 0,4x – 0,6x = 0,9 – 1,2

-0,1x = -0,3

x = -0,3 : (-0,1)

x = 3

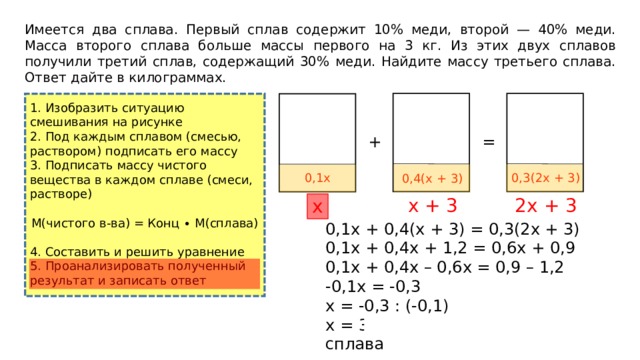
Имеется два сплава. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым сплавом (смесью, раствором) подписать его массу

3. Подписать массу чистого вещества в каждом сплаве (смеси, растворе)

М(чистого в-ва) = Конц ∙ М(сплава)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

+

=

0,3(2x + 3)

0,1x

0,4(x + 3)

x + 3

2x + 3

x

0,1х + 0,4(x + 3) = 0,3(2x + 3)

0,1x + 0,4x + 1,2 = 0,6x + 0,9

0,1x + 0,4x – 0,6x = 0,9 – 1,2

-0,1x = -0,3

x = -0,3 : (-0,1)

x = 3 (кг) – масса первого сплава

Имеется два сплава. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым сплавом (смесью, раствором) подписать его массу

3. Подписать массу чистого вещества в каждом сплаве (смеси, растворе)

М(чистого в-ва) = Конц ∙ М(сплава)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

+

=

0,3(2x + 3)

0,1x

0,4(x + 3)

x + 3

2x + 3

x

0,1х + 0,4(x + 3) = 0,3(2x + 3)

0,1x + 0,4x + 1,2 = 0,6x + 0,9

0,1x + 0,4x – 0,6x = 0,9 – 1,2

-0,1x = -0,3

x = -0,3 : (-0,1)

x = 3 (кг) – масса первого сплава

2х + 3 = 2 ∙ 3 + 3 = 9 (кг). Ответ: 9

Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

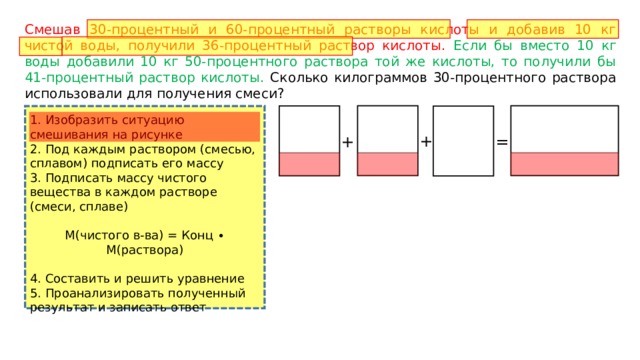
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

+

=

+

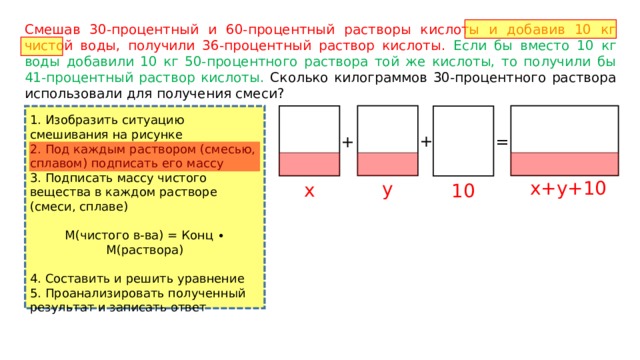
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

+

+

=

x+y+10

y

x

10

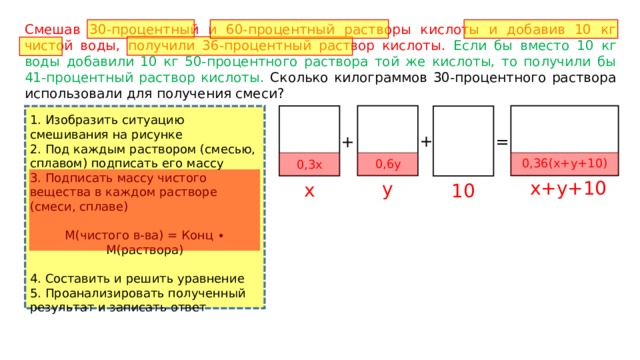
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

+

+

=

0,36(x+y+10)

0,6y

0,3x

x+y+10

y

x

10

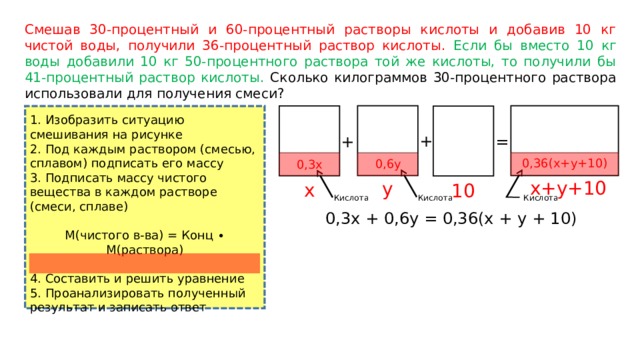
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

+

+

=

0,36(x+y+10)

0,6y

0,3x

x+y+10

y

x

10

Кислота

Кислота

Кислота

0,3х + 0,6y = 0,36(x + y + 10)

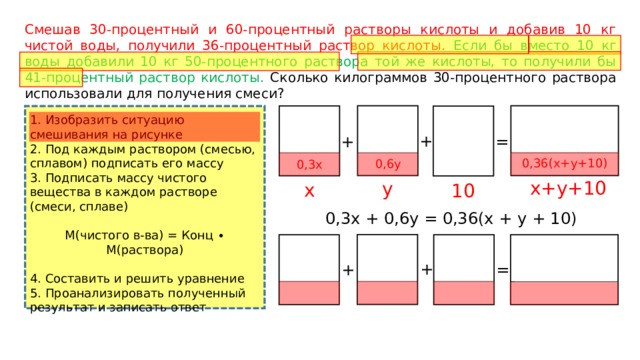
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

+

=

+

0,36(x+y+10)

0,6y

0,3x

x+y+10

y

x

10

0,3х + 0,6y = 0,36(x + y + 10)

+

=

+

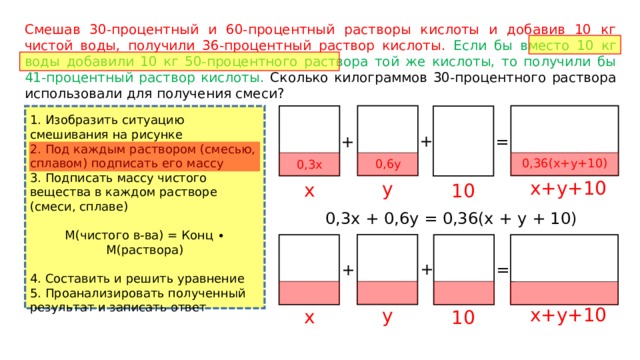
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

+

+

=

0,36(x+y+10)

0,6y

0,3x

x+y+10

y

x

10

0,3х + 0,6y = 0,36(x + y + 10)

+

+

=

x+y+10

y

x

10

Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

+

=

+

0,36(x+y+10)

0,6y

0,3x

x+y+10

y

x

10

0,3х + 0,6y = 0,36(x + y + 10)

+

=

+

0,41(x+y+10)

0,6y

0,5 ∙ 10

0,3x

x+y+10

y

x

10

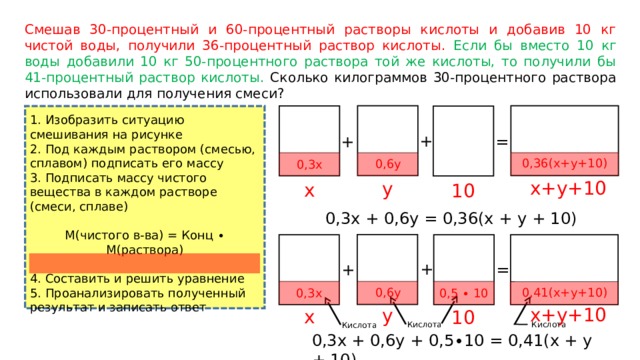
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

+

=

+

0,36(x+y+10)

0,6y

0,3x

x+y+10

y

x

10

0,3х + 0,6y = 0,36(x + y + 10)

+

+

=

0,6y

0,41(x+y+10)

0,5 ∙ 10

0,3x

x+y+10

y

x

10

Кислота

Кислота

Кислота

0,3х + 0,6y + 0,5∙10 = 0,41(x + y + 10)

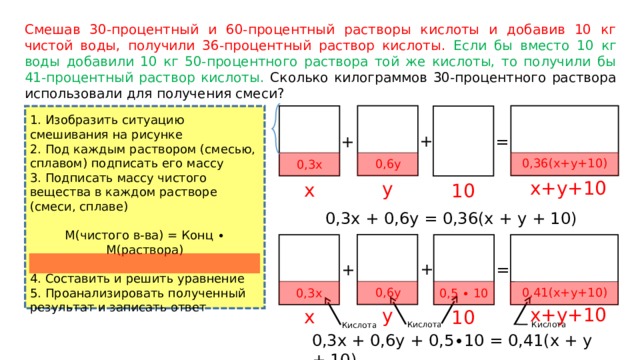
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

+

=

+

0,36(x+y+10)

0,6y

0,3x

x+y+10

y

x

10

0,3х + 0,6y = 0,36(x + y + 10)

+

=

+

0,6y

0,41(x+y+10)

0,5 ∙ 10

0,3x

x+y+10

y

x

10

Кислота

Кислота

Кислота

0,3х + 0,6y + 0,5∙10 = 0,41(x + y + 10)

Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

0,3х + 0,6y = 0,36(x + y + 10)

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

0,3х + 0,6y + 0,5∙10 = 0,41(x + y + 10)

0,3х + 0,6y = 0,36x + 0,36y + 3,6

0,3х + 0,6y + 5 = 0,41x + 0,41y + 4,1

0,3х – 0,36х + 0,6y – 0,36y = 3,6

0,3х – 0,41x + 0,6y – 0,41y = 4,1 – 5

Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

0,3х – 0,36х + 0,6y – 0,36y = 3,6

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

0,3х – 0,41x + 0,6y – 0,41y = 4,1 – 5

– 0,06х + 0,24y = 3,6

| ∙ 100

| ∙ 100

– 0,11x + 0,19y = – 0,9

– 6х + 24y = 360

– 11x + 19y = – 90

Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

| : (–6)

– 6х + 24y = 360

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

– 11х + 19y = – 90

| ∙ 11

х – 4y = – 60

– 11х + 19y = – 90

11х – 44y = – 660

– 11х + 19y = – 90

– 25y

=

– 750

y = – 750 : (– 25) = 30

Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

| : (–6)

– 6х + 24y = 360

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

– 11х + 19y = – 90

| ∙ 11

= – 60

y

х – 4

х – 4y = – 60

– 11х + 19y = – 90

11х – 44y = – 660

– 11х + 19y = – 90

– 25y

=

– 750

∙ 30

y = – 750 : (– 25) = 30

Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

| : (–6)

– 6х + 24y = 360

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

– 11х + 19y = – 90

| ∙ 11

= – 60

y

х – 4y = – 60

х – 4

– 11х + 19y = – 90

х – 120 = – 60

11х – 44y = – 660

х = – 60 + 120

– 11х + 19y = – 90

х = 60

– 25y

=

– 750

y = – 750 : (– 25) = 30

Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

| : (–6)

– 6х + 24y = 360

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

– 11х + 19y = – 90

| ∙ 11

= – 60

y

х – 4

х – 4y = – 60

– 11х + 19y = – 90

х – 120 = – 60

11х – 44y = – 660

х = – 60 + 120

– 11х + 19y = – 90

х = 60

х = 60;

– 25y

=

– 750

y =

30

y = – 750 : (– 25) = 30

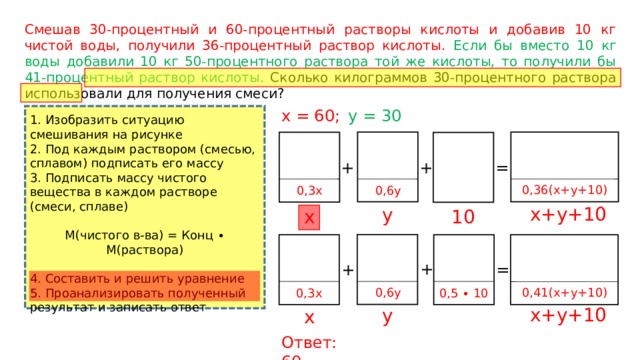
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

y = 30

х = 60;

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

+

+

=

0,36(x+y+10)

0,6y

0,3x

x+y+10

y

x

10

+

+

=

0,6y

0,41(x+y+10)

0,5 ∙ 10

0,3x

x+y+10

y

x

Ответ: 60.

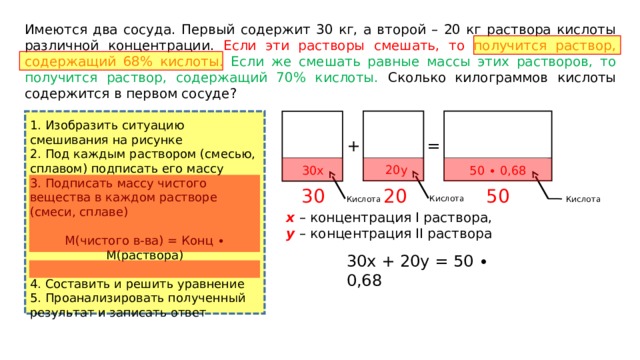
Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

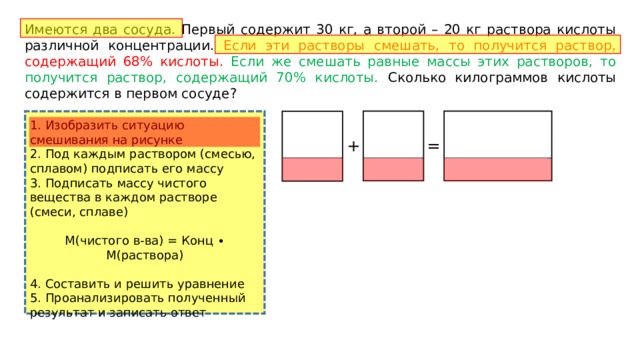
Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

=

+

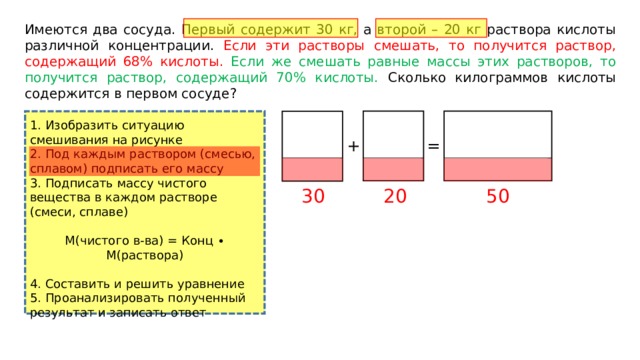
Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

=

+

50

20

30

Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

=

+

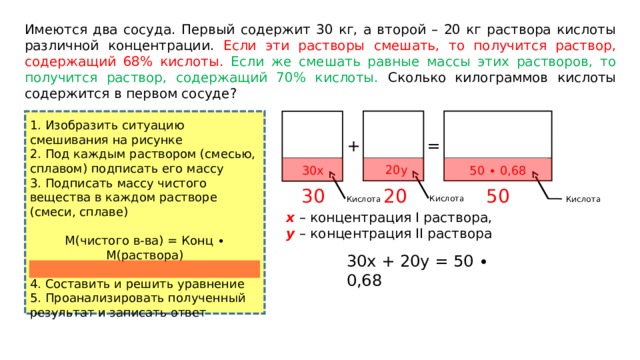
20y

30x

50 ∙ 0,68

50

20

30

Кислота

Кислота

Кислота

x – концентрация I раствора,

y – концентрация II раствора

30х + 20y = 50 ∙ 0,68

Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

=

+

20y

30x

50 ∙ 0,68

50

20

30

Кислота

Кислота

Кислота

x – концентрация I раствора,

y – концентрация II раствора

30х + 20y = 50 ∙ 0,68

Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

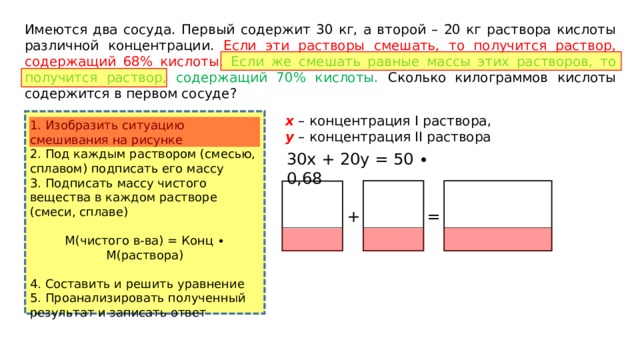
x – концентрация I раствора,

y – концентрация II раствора

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

30х + 20y = 50 ∙ 0,68

=

+

Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

x – концентрация I раствора,

y – концентрация II раствора

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

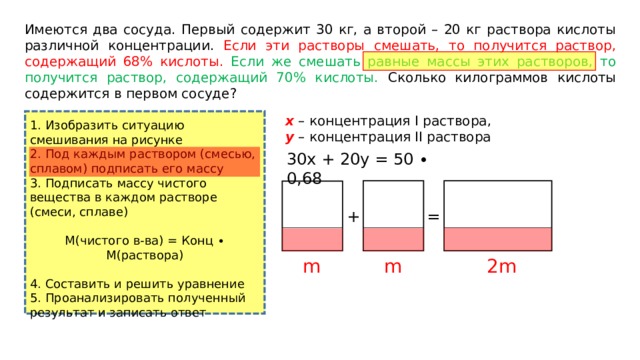
30х + 20y = 50 ∙ 0,68

=

+

2m

m

m

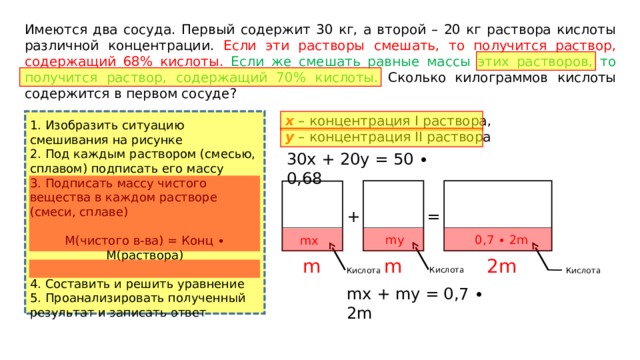
Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

x – концентрация I раствора,

y – концентрация II раствора

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

30х + 20y = 50 ∙ 0,68

=

+

my

0,7 ∙ 2m

mx

2m

m

m

Кислота

Кислота

Кислота

mх + my = 0,7 ∙ 2m

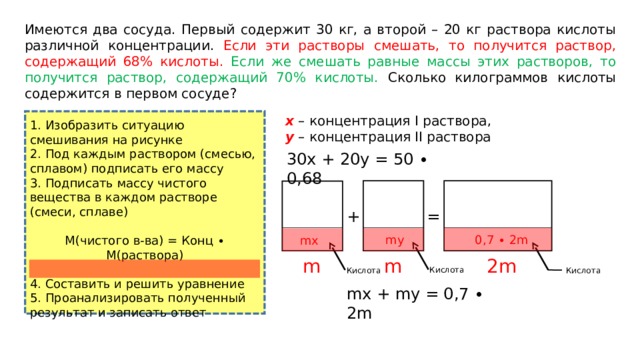
Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

x – концентрация I раствора,

y – концентрация II раствора

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

30х + 20y = 50 ∙ 0,68

=

+

my

0,7 ∙ 2m

mx

2m

m

m

Кислота

Кислота

Кислота

mх + my = 0,7 ∙ 2m

Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

x – концентрация I раствора,

y – концентрация II раствора

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

30х + 20y = 50 ∙ 0,68

mх + my = 0,7 ∙ 2m

| : m

30х + 20y = 34

х + y = 1,4

| ∙ (– 20)

30х + 20y = 34

– 20х – 20y = – 28

10x

=

6

x = 6 : 10 = 0,6

Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

x = 0,6

y = 0,8

x – концентрация I раствора,

y – концентрация II раствора

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

30х + 20y = 50 ∙ 0,68

mх + my = 0,7 ∙ 2m

| : m

30х + 20y = 34

| ∙ (– 20)

+ y

= 1,4

х + y = 1,4

х

30х + 20y = 34

– 20х – 20y = – 28

y = 1,4 – 0,6

y = 0,8

=

6

10x

0,6

x = 6 : 10 = 0,6

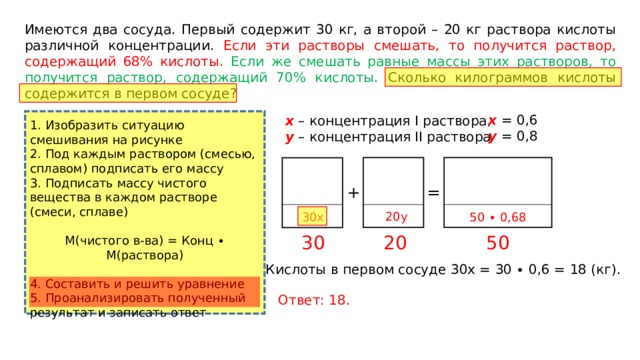
Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

x = 0,6

y = 0,8

x – концентрация I раствора,

y – концентрация II раствора

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

=

+

20y

30x

50 ∙ 0,68

50

20

30

Кислоты в первом сосуде 30х = 30 ∙ 0,6 = 18 (кг).

Ответ: 18.

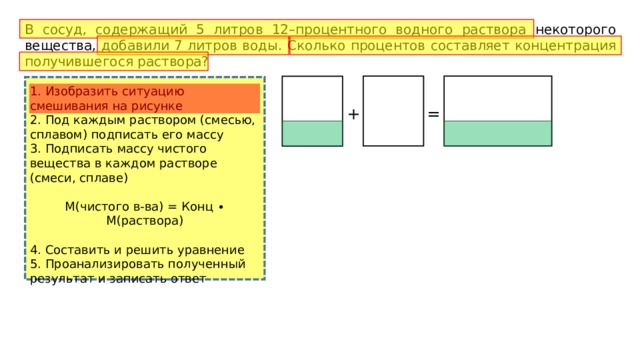
В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

=

+

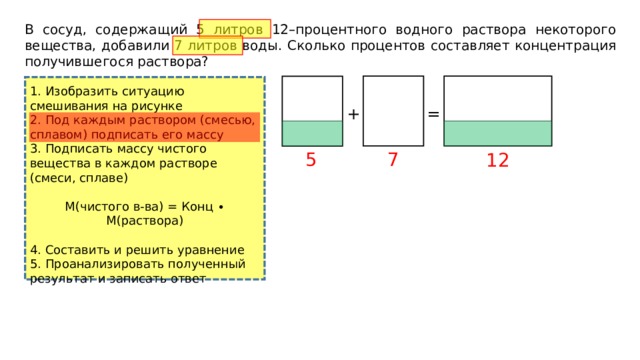
В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

=

+

5

7

12

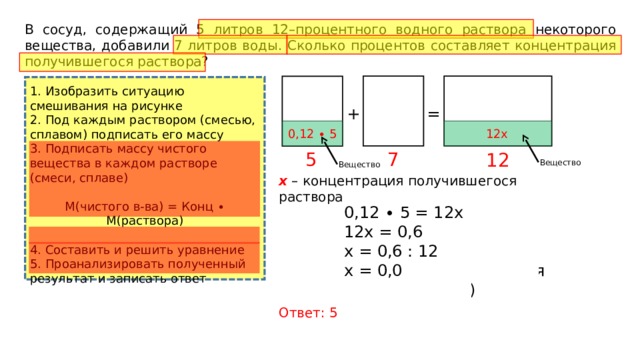
В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

=

+

12x

0,12 ∙ 5

7

5

12

Вещество

Вещество

x – концентрация получившегося раствора

0,12 ∙ 5 = 12х

12х = 0,6

х = 0,6 : 12

х = 0,05 (концентрация составляет 5%)

Ответ: 5

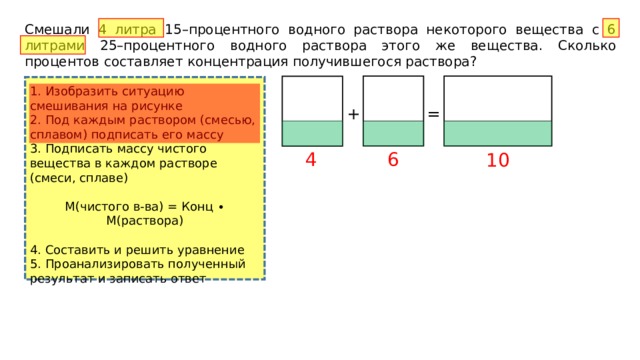
Смешали 4 литра 15–процентного водного раствора некоторого вещества с 6 литрами 25–процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

=

+

4

6

10

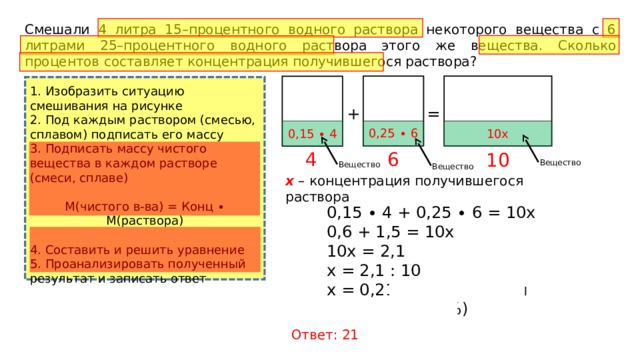
Смешали 4 литра 15–процентного водного раствора некоторого вещества с 6 литрами 25–процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

=

+

0,25 ∙ 6

0,15 ∙ 4

10x

4

6

10

Вещество

Вещество

Вещество

x – концентрация получившегося раствора

0,15 ∙ 4 + 0,25 ∙ 6 = 10х

0,6 + 1,5 = 10x

10x = 2,1

x = 2,1 : 10

x = 0,21 (концентрация составляет 21%)

Ответ: 21

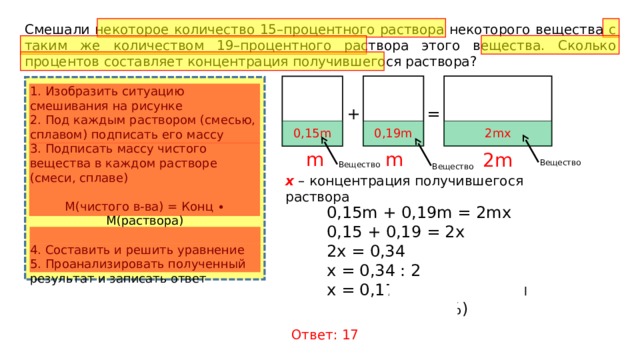
Смешали некоторое количество 15–процентного раствора некоторого вещества с таким же количеством 19–процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

1. Изобразить ситуацию смешивания на рисунке

2. Под каждым раствором (смесью, сплавом) подписать его массу

3. Подписать массу чистого вещества в каждом растворе (смеси, сплаве)

М(чистого в-ва) = Конц ∙ М(раствора)

4. Составить и решить уравнение

5. Проанализировать полученный результат и записать ответ

=

+

0,15m

0,19m

2mx

m

m

2m

Вещество

Вещество

Вещество

x – концентрация получившегося раствора

0,15m + 0,19m = 2mх | :m

0,15 + 0,19 = 2x

2x = 0,34

x = 0,34 : 2

x = 0,17 (концентрация составляет 17%)

Ответ: 17