Презентация "Развертка призмы"

Развёртка – развёрнутая в плоскость поверхность какого-либо тела. Площадь развёртки равна площади поверхности.

Развёртка многогранника – совокупность многоугольников, соответственно равных граням многогранника. Взаимное расположение многоугольников на развёртке может иметь несколько вариантов.

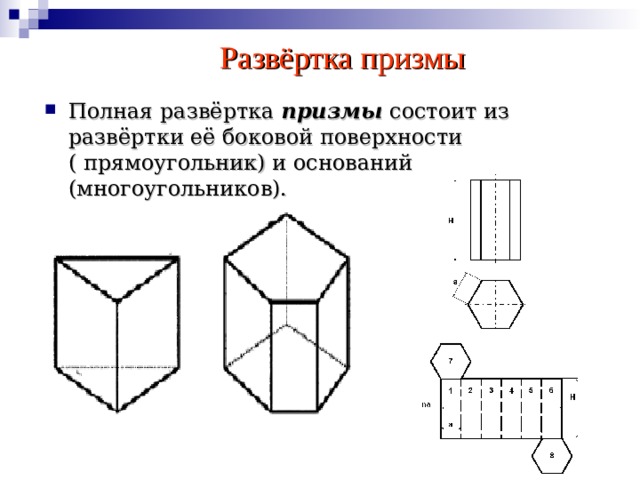
Развёртка призмы

• Полная развёртка призмы состоит из развёртки её боковой поверхности ( прямоугольник) и оснований (многоугольников).

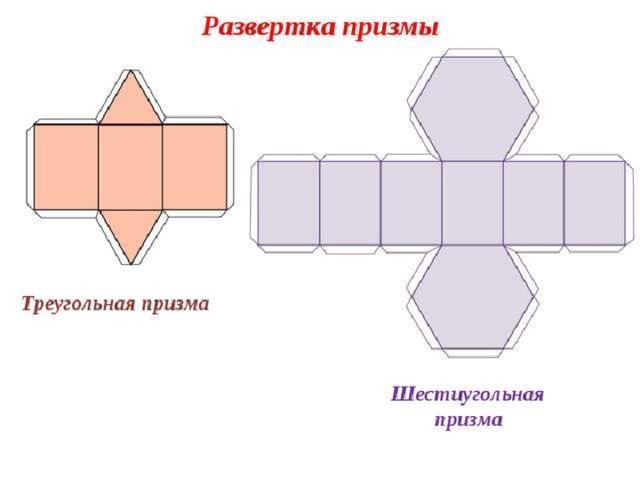
При построении развёртки боковой поверхности призмы используются 2 способа:

- способ нормального сечения;

- способ раскатки;

Способ нормального сечения

используют для развертки поверхности призм общего положения. В этом случае строится нормальное сечение призмы (т.е. вводится плоскость, расположенная перпендикулярно боковым ребрам призмы) и определяются натуральные величины сторон многоугольника этого нормального сечения.

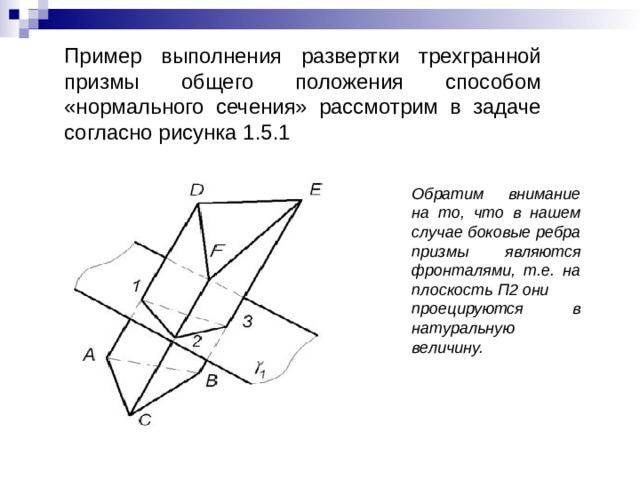
Пример выполнения развертки трехгранной призмы общего положения способом «нормального сечения» рассмотрим в задаче согласно рисунка 1.5.1

Обратим внимание на то, что в нашем случае боковые ребра призмы являются фронталями, т.е. на плоскость П2 они проецируются в натуральную величину.

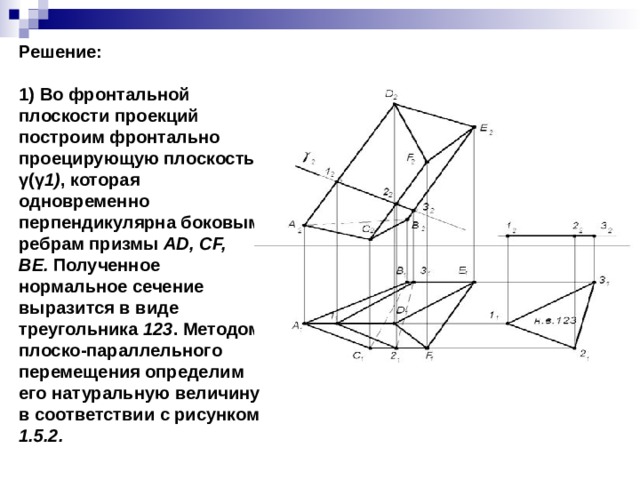
Решение:

1) Во фронтальной плоскости проекций построим фронтально проецирующую плоскость γ(γ 1) , которая одновременно перпендикулярна боковым ребрам призмы  AD, CF, BE.  Полученное нормальное сечение выразится в виде треугольника  123 . Методом плоско-параллельного перемещения определим его натуральную величину в соответствии с рисунком 1.5.2.

2) Все стороны нормального сечения последовательно отложим на прямой:  1020=111211; 2030=211311; 3010=311111. 3) Через точки  10,20,30  проведем прямые, перпендикулярные прямой  10-10  и отложим на них натуральную величину боковых ребер:  10D0 =12D2  и  10A0 = 12A2; 20F0 = 22F2  и  20C0 = 22C2; 30E0 = 32E2  и  30B0 = 32B2 . 4) Полученные точки верхнего и нижнего оснований призмы соединим прямыми  A0B0C0  и  D0F0E0 . Плоская фигура  A0B0C0D0F0E0  является искомой разверткой боковой поверхности данной призмы. Для построения полной развертки необходимо к развертке боковой поверхности пристроить натуральные величины оснований. Для этого воспользуемся полученными на развертке натуральными величинами их сторон  A0C0, C0B0, B0A0  и  D0F0, F0E0, E0D0  в соответствии с рисунком 1.5.3

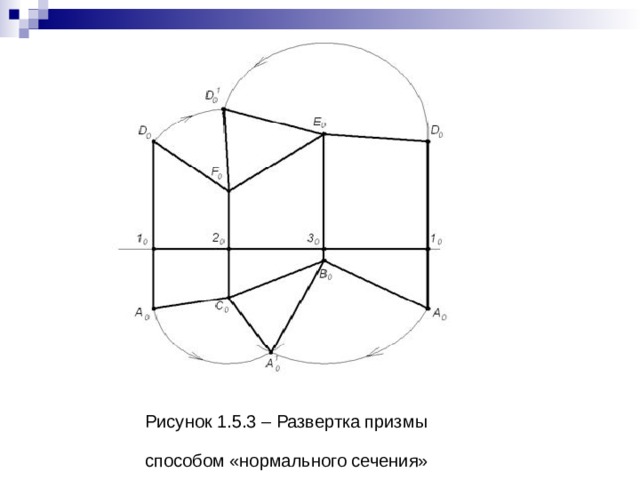
Рисунок 1.5.3 – Развертка призмы способом «нормального сечения»

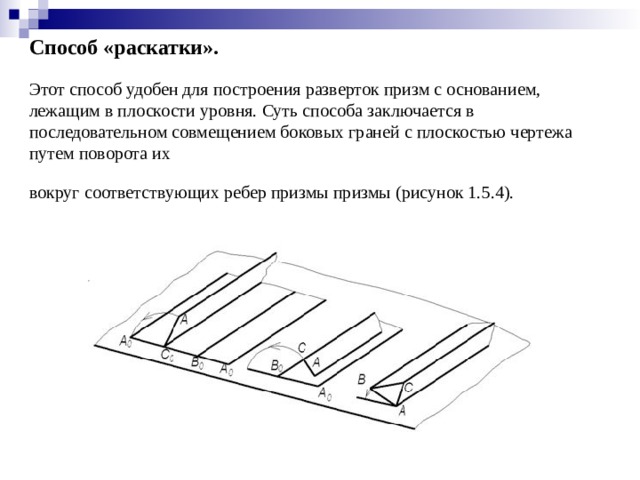
Способ «раскатки».   Этот способ удобен для построения разверток призм с основанием, лежащим в плоскости уровня. Суть способа заключается в последовательном совмещением боковых граней с плоскостью чертежа путем поворота их вокруг соответствующих ребер призмы призмы (рисунок 1.5.4).

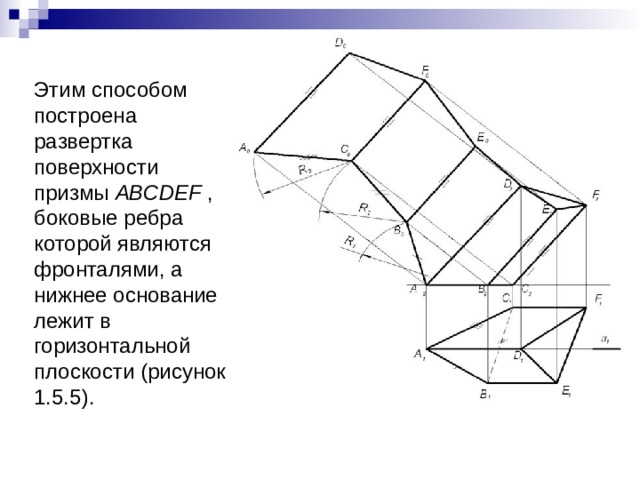
Этим способом построена развертка поверхности призмы  ABCDEF  , боковые ребра которой являются фронталями, а нижнее основание лежит в горизонтальной плоскости (рисунок 1.5.5).

• Решение:

• Боковые грани призмы совместим с фронтальной плоскостью, проходящей через ребро  AD . Это удобно в этом случае, т.к. фронтальные проекции боковых ребер призмы равны их истинной длине. Тогда ребро  A0D0 развертки будет совпадать с фронтальной проекцией ребра  AD(A2D2) .
• Для определения на развертке истиной величины боковой грани  ADEB  вращаем ее вокруг ребра  AD  до положения, параллельного фронтальной плоскости проекций. Чтобы определить на развертке положение точки  B0 , из точки  B2  восстанавливаем перпендикуляр к  A2D2 . Точка  B0  будет найдена в пересечении этого перпендикуляра с дугой окружности радиуса  R1 , равного истиной величине ребра  AB  и проведенной из точки  A2 , как из центра.

• 3) Точка  E0  будет определяться на развертке как результат пересечения прямой  B0E0  параллельной фронтальной проекцией ребра  BE(B2E2),  и перпендикуляра, восстановленного из точки  E2  к  A2D2.
• 4) Точки  C0  и  A0  построены аналогично точке  B0  в пересечении перпендикуляров из точек  C2  и  A2  к фронтальным проекциям ребер, с дугами окружностей, проведенных из точек  B0  и  C0  как из центров радиусами  R2  и  R3 , равными соответственно ребрам  BC  и  CA . Точки  F0  и  D0  определяются аналогично точке  E0 .

• 5) Соединив последовательно совмещенные вершины ломаными линиями, получим развертку боковой поверхности призмы  A0B0C0A0D0F0E0D0 . При необходимости можно получить полную развертку призмы, присоединив к ней натуральные величины обоих оснований.
• Если боковые ребра призмы занимают общее положение, то предварительным преобразованием чертежа их надо привести в положение линий уровня.