Презентация Решение задач по теме трапеция.

• Решение задач

Трапеция

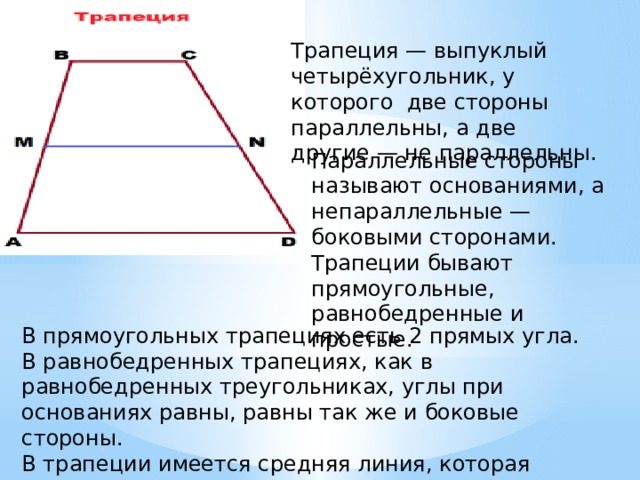
Трапеция — выпуклый четырёхугольник, у которого  две стороны параллельны, а две другие — не параллельны.

Параллельные стороны называют основаниями, а непараллельные — боковыми сторонами. Трапеции бывают прямоугольные, равнобедренные и простые.

В прямоугольных трапециях есть 2 прямых угла. В равнобедренных трапециях, как в равнобедренных треугольниках, углы при основаниях равны, равны так же и боковые стороны. В трапеции имеется средняя линия, которая соединяет середины боковых сторон.

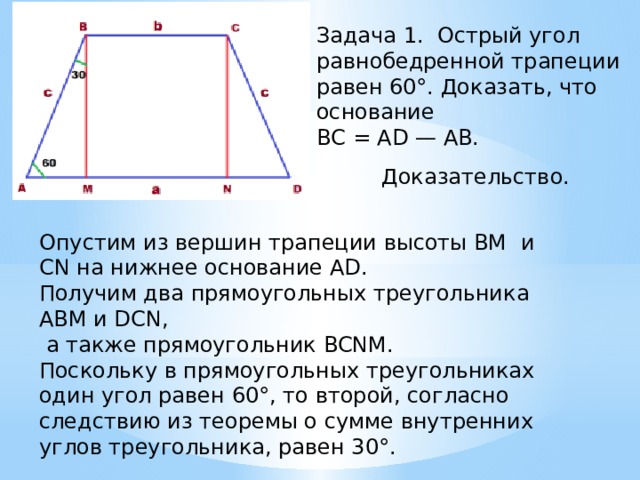
Задача 1.  Острый угол равнобедренной трапеции равен 60°. Доказать, что основание

ВС = AD — AB.

Доказательство.  

Опустим из вершин трапеции высоты BM  и CN на нижнее основание AD. Получим два прямоугольных треугольника ABM и DCN,

а также прямоугольник BCNM. Поскольку в прямоугольных треугольниках один угол равен 60°, то второй, согласно следствию из теоремы о сумме внутренних углов треугольника, равен 30°.

А мы знаем, что катет, лежащий против угла в 30°, равен половине гипотенузы. Т.е. АМ= с/2. То же самое и в правом треугольнике — ND = с/2. Получается, что нижнее основание можно представить в виде суммы трёх отрезков, а именно AM, MN, ND, где AM=ND=c/2. MN=BC, или верхнему основанию. Отсюда можно написать MN=BC=AD — AM — ND =

AD — c/2 — c/2 = AD — AB. Мы доказали, что верхнее основание равно разности нижнего основания и боковой стороны.

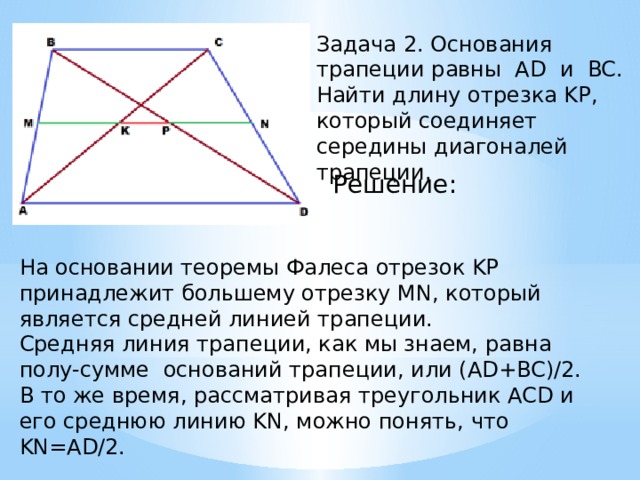
Задача 2. Основания трапеции равны  AD  и  BC. Найти длину отрезка KP, который соединяет середины диагоналей трапеции.

Решение:  

На основании теоремы Фалеса отрезок KP принадлежит большему отрезку MN, который является средней линией трапеции. Средняя линия трапеции, как мы знаем, равна полу-сумме  оснований трапеции, или (AD+BC)/2. В то же время, рассматривая треугольник ACD и его среднюю линию KN, можно понять, что KN=AD/2.

Рассматривая другой треугольник BCD и его среднюю линию PN, можно увидеть, что PN=BC/2. Отсюда, KP=KN-PN = AD/2 — BC/2 =

(AD-BC)/2. Мы доказали, что отрезок, который соединяет середины диагоналей трапеции, равен полу-разности оснований данной трапеции.

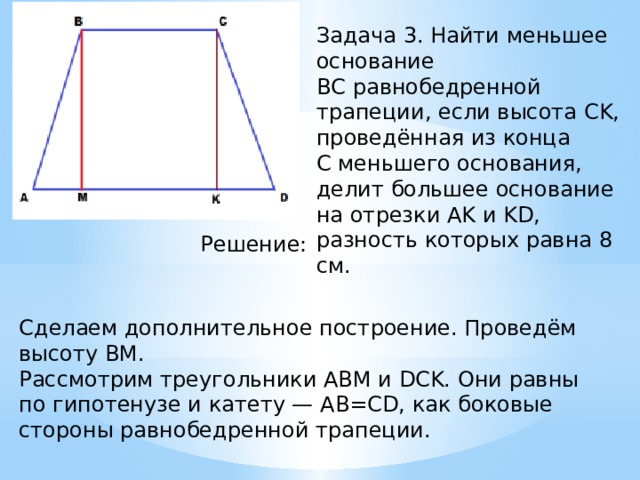
Задача 3. Найти меньшее основание ВС равнобедренной трапеции, если высота СK, проведённая из конца C меньшего основания, делит большее основание на отрезки AK и KD, разность которых равна 8 см.

Решение: 

Сделаем дополнительное построение. Проведём высоту ВМ. Рассмотрим треугольники ABM и DCK. Они равны по гипотенузе и катету — AB=CD, как боковые стороны равнобедренной трапеции.

Высоты трапеции BM и CK тоже равны, как перпендикуляры, расположенные между двумя параллельными прямыми. Следовательно, AM=KD. Получается, что разность между AK и KD равна разности между AK и AM. А это есть отрезок MK. Но MK равен ВС, поскольку BCKM — прямоугольник. Отсюда меньшее основание трапеции равно 8 см.

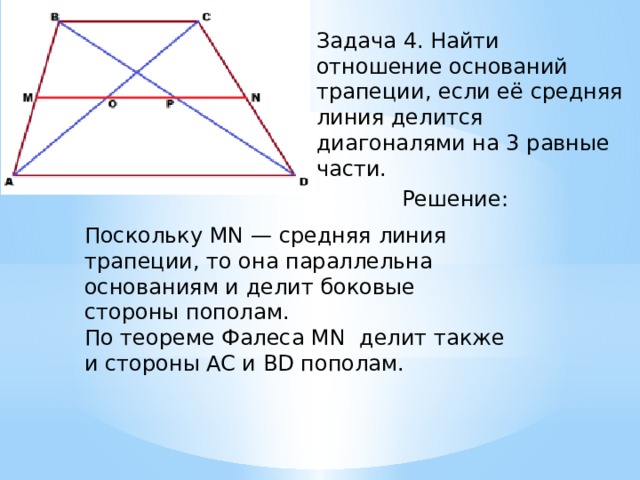
Задача 4. Найти отношение оснований трапеции, если её средняя линия делится диагоналями на 3 равные части.

Решение:  

Поскольку MN — средняя линия трапеции, то она параллельна основаниям и делит боковые стороны пополам. По теореме Фалеса MN  делит также и стороны AC и BD пополам.

Рассматривая треугольник АВС можно видеть, что MO в нём — средняя линия. А средняя линия треугольника параллельна  основанию и равна его половине. Т.е. если MO=Х, то ВС=2Х. Из треугольника ACD имеем ON — средняя линия. Она тоже параллельна основанию и равна его половине. Но, поскольку OP+PN= Х+Х=2Х, тогда AD=4Х. Получается, что верхнее основание трапеции равно 2Х, а нижнее — 4Х. Ответ: отношение оснований трапеции равно 1:2