Презентация : "Сфера и Шар"

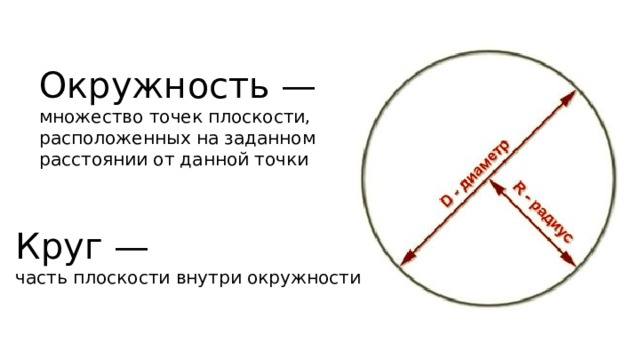
Окружность —

множество точек плоскости, расположенных на заданном расстоянии от данной точки

Круг —

часть плоскости внутри окружности

Сфера —

поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки

C

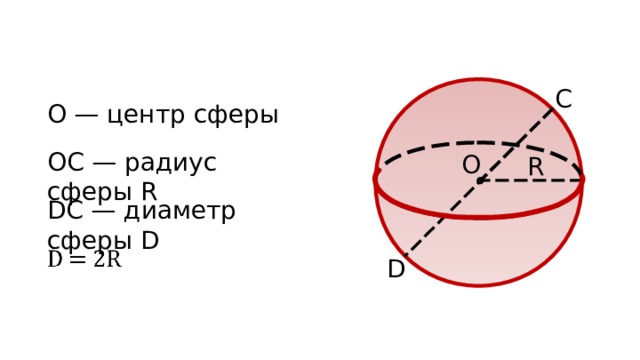
О — центр сферы

ОС — радиус сферы R

O

R

DC — диаметр сферы D

D

Шар —

тело, ограниченное сферой

O

Шар радиуса R с центром в точке О —

тело, содержащее все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О) , и не содержит других точек

Центр, радиус, диаметр сферы — центр, радиус, диаметр шара

A

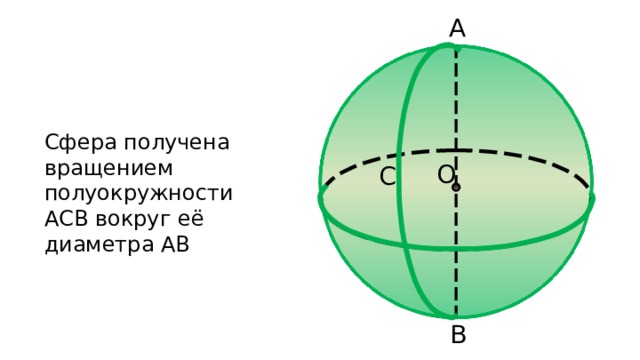
Сфера получена вращением полуокружности АСВ вокруг её диаметра АВ

O

C

B

Задача 1

B

M

Доказательство:

A

O

△ АОВ — равнобедренный

Что требовалось доказать

Задача 2

M

A

B

Найти: расстояние от центра сферы до АВ

Решение:

1) Д.п. проведём плоскость АВО

R

R

Сечение — окружность радиуса r

Д.п. ОМ — высота, медиана

O

ОМ — расстояние от точки О до прямой АВ

по теореме Пифагора:

4) △ АОМ — прямоугольный,