Презентация: "Сочетания"

Сочетания без повторений

Авторы проекта

2010

Сочетания без повторений

• к-элементные подмножества n- элементного множества X называются сочетаниями без повторений из элементов этого множества по к. Их число обозначают

Пример

,

c

c

c

b

b

a

}

e

d

d

e

c

a

,

b

a

c

,

,

a

b

{

можно составить 10 сочетаний по 3 элемента в каждом

e

d

c

c

d

b

c

e

b

e

d

b

c

a

d

a

e

c

a

e

d

{a, b, c, d, e}

Из предыдущего примера видно, что число размещений без повторений из 5 элементов по 3 равно

что согласуется с формулой

Найдем число сочетаний без повторений из n элементов по k

Из каждого сочетания без повторений из n по k путем упорядочиваний получаются k! различных размещений без повторений из n элементов по k .

Отсюда следует, что число размещений без повторений из n элементов по k в k! раз больше, чем число сочетаний без повторений из n элементов по k .

Иными словами, мы доказали, что

Но тогда

Подставляя для

Пример 1

• Сколькими способами можно поставить на шахматную доску восемь ладей? Не налагается условие, что ладьи не могут бить друг друга. Поэтому нам надо просто выбрать из 64 клеток шахматной доски любые восемь клеток. А это может быть сделано

способами.

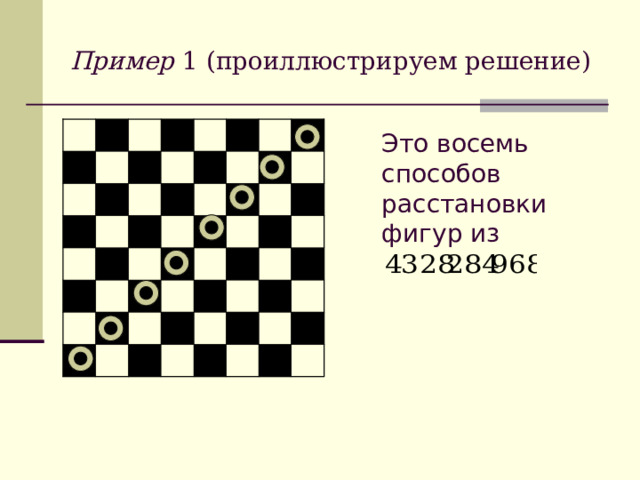
Пример 1 ( проиллюстрируем решение )

Это восемь способов расстановки фигур из

Пример 2

• Точно также доказывается, что на доске из m горизонталей и n вертикалей k ладей можно поставить

способами.

• Если же ставить не k одинаковых ладей, а k различных фигур, то уже важно, какая фигура куда поставлена. Поэтому в этом случае имеем не сочетание , а размещения, и ответ дается формулой

Многие комбинаторные задачи сводятся к подсчету числа сочетаний без повторений из n элементов по k .

Пример 3

• Сколькими способами можно выбрать 5 делегатов из состава конференции, на которой присутствует 15 человек?

Число способов выбора делегатов равно: