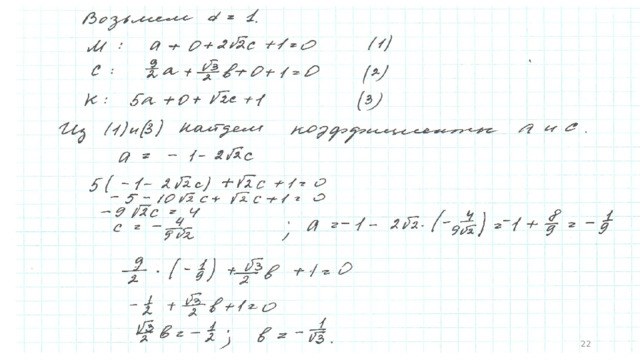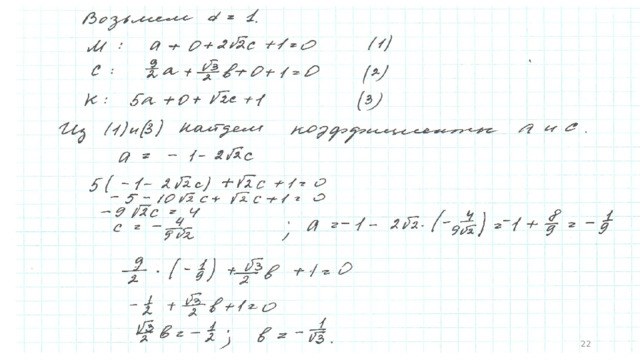Презентация "Стереометрия: координатно-векторный метод", задание № 14 ЕГЭ по математике, профильный уровень

Задание №14 ЕГЭ по математике,

профильный уровень

Стереометрия:

координатно-векторный метод

1. Точки 𝑁 и 𝑀 — середины рёбер 𝐴𝐷 и 𝐶𝐶 1 куба 𝐴𝐵𝐶𝐷𝐴 1 𝐵 1 𝐶 1 𝐷 1 соответственно. Доказать, что 𝐵𝑀 ⊥ 𝐵 1 𝑁

2. В основании четырёхугольной пирамиды 𝑆𝐴𝐵𝐶𝐷 лежит прямоугольник 𝐴𝐵𝐶𝐷 со сторонами 𝐴𝐵 = 12 и 𝐵𝐶 = 5√3. Длины боковых рёбер пирамиды 𝑆𝐴=5, 𝑆𝐵 = 13 , 𝑆𝐷 = 10. а) Докажите, что 𝑆𝐴 — высота пирамиды. б) Найдите расстояние от вершины 𝐴 до плоскости 𝑆𝐵𝐶.

3. Боковое ребро правильной треугольной пирамиды 𝑆𝐴𝐵𝐶 равно 10, а косинус угла 𝐴𝑆𝐵 равен 17/25 . Точка 𝑀 — середина ребра 𝑆𝐶. а) Докажите, что 𝐵𝑆 ⊥ 𝐴𝐶. б) Найдите угол между прямыми 𝐵𝑀 и 𝑆𝐴.

4. В кубе 𝐴𝐵𝐶𝐷𝐴 1 𝐵 1 𝐶 1 𝐷 1 точки 𝑀 и 𝑁 являются серединами рёбер 𝐴𝐵 и 𝐴𝐷 соответственно. a) Докажите, что прямые 𝐵 1 𝑁и 𝐶𝑀 перпендикулярны. б) Плоскость 𝛼 проходит через точки 𝑁 и 𝐵 1 параллельно прямой 𝐶𝑀. Найдите расстояние от точки 𝐶 до плоскости 𝛼, если 𝐵 1 𝑁 = 6 .

5. В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷𝐴 1 𝐵 1 𝐶 1 𝐷 1 на диагонали 𝐵𝐷 1 отмечена точка 𝑁 так, что 𝐵𝑁 : 𝑁𝐷 1 = 1 : 2. Точка 𝑂 – середина отрезка 𝐶𝐵 1 . a) Докажите, что прямая 𝑁𝑂 проходит через точку А.

6. Дана правильная четырехугольная призма 𝐴𝐵𝐶𝐷𝐴 1 𝐵 1 𝐶 1 𝐷 1 . На ребре 𝐴𝐴 1 отмечена точка 𝐾 так, что 𝐴𝐾 : 𝐾𝐴 1 = 1 : 2. Плоскость 𝛼 проходит через точки 𝐵 и 𝐾 параллельно прямой 𝐴𝐶. Эта плоскость пересекает ребро 𝐷𝐷 1 в точке 𝑀. а) Докажите, что 𝑀𝐷 : 𝑀𝐷 1 = 2 : 1.

7. Дана прямая призма, в основании которой равнобедренная трапеция с основаниями 𝐴𝐷 = 5 и 𝐵𝐶 = 4. Точка 𝑀 делит ребро 𝐴 1 𝐷 1 в отношении 𝐴 1 𝑀 : 𝑀𝐷 1 = 1 : 4, точка 𝐾 – середина 𝐷𝐷 1 . б) Найти тангенс угла между плоскостью 𝑀𝐾𝐶 и плоскостью основания, если ∠𝐵𝐴𝐷 = 60∘ , a ∠𝐶𝐾М=90∘.