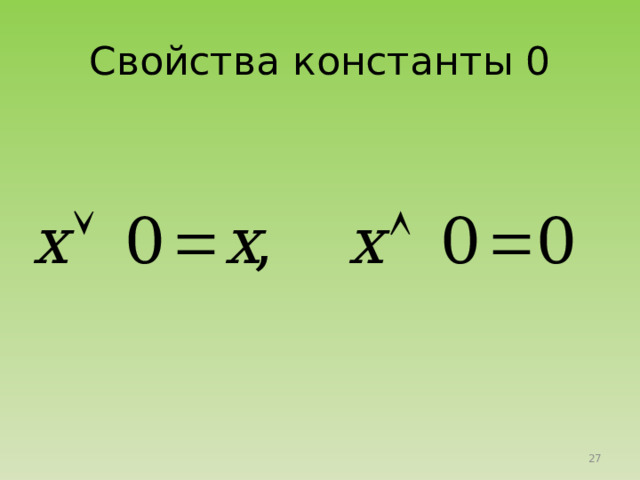Презентация: Упрощение булевых функций

Булевы функции

План:

• Упрощение булевых функций

Способы задания булевых функций

• табличный;
• графический;
• аналитический.

• Элементарными конъюнкциями называются….

• Дизъюнктивной нормальной формой (ДНФ) называется формула, имеющая …..

• Элементарными дизъюнкциями называются …..

• Конъюнктивной нормальной формой (КНФ) называется формула, имеющая вид …..

ДНФ (КНФ) представляет формулу неоднозначно. Частным случаем ДНФ является совершенная ДНФ (СДНФ) – однозначное представление формул логики высказываний.

Совершенная ДНФ (СДНФ) – ДНФ, в которой нет одинаковых элементарных конъюнкций и все конъюнкции состоят из одного и того же набора переменных, в который каждая переменная входит только один раз (возможно с отрицанием).

Пример записи формулы с СДНФ: (А&B&С) ∨(A&B& ┐C).

Совершенная КНФ (СКНФ) – КНФ, в которой нет одинаковых элементарных дизъюнкций и все дизъюнкции состоят из одного и того же набора переменных, в который каждая переменная входит только один раз (возможно с отрицанием).

Пример записи формулы с СКНФ: (A ∨B∨ ┐C) &(A ∨C∨B)

Методика представления булевой функции в нормальной форме и совершенной нормальной форме.

• Если булева функция задана таблицей истинности, то она может быть представлена в аналитической форме с использованием операций конъюнкции, дизъюнкции и инверсии с помощью следующих правил:

Алгоритм получения СДНФ по таблице истинности:

Шаг 1: Отметить те строки таблицы истинности, в которых формула принимает значение «истина» (λ(F) = 1).

Шаг 2: Выписать для каждой отмеченной строки конъюнкцию всех переменных следующим образом: если значение некоторой переменной в данной строке равно «истине», то в конъюнкцию включают саму эту переменную, иначе – ее отрицание.

Шаг 3: Все полученные конъюнкции связать в дизъюнкцию.

– каждой единице в таблице истинности сопоставляется конъюнкция ранга n , где n – число аргументов функции; рангом конъюнкции называют число аргументов, входящих в конъюнкцию, причем в эту конъюнкцию аргумент входит без инверсии, если в соответствующем наборе он принимает значение 1, и с инверсией, если принимает значение 0;

– все полученные конъюнкции объединяются знаками дизъюнкции.

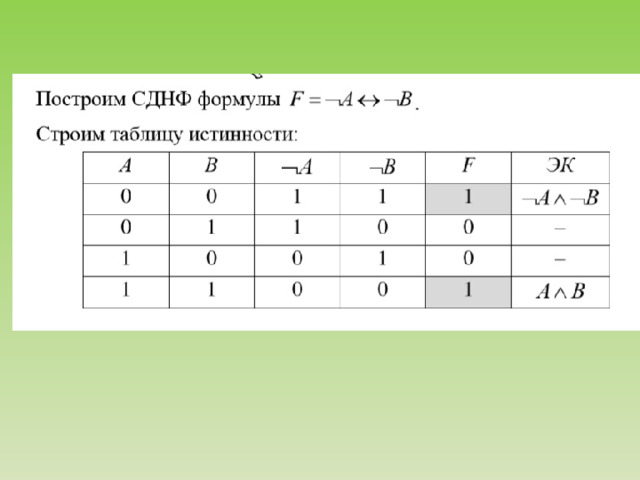
Такое аналитическое выражение функции называют совершенной дизъюнктивной нормальной формой (СДНФ) функции, при этом под нормальной формой понимают выражение, в котором инверсии применяются только к отдельным аргументам, под совершенной формой понимают аналитическое выражение функции, когда во все конъюнкции входят все аргументы, т. е. все конъюнкции имеют ранг n .

Если в таблице истинности число нулей существенно меньше числа единиц, используют аналитическую запись в виде совершенной конъюнктивной нормальной формы (СКНФ).

Алгоритм получения СКНФ по таблице истинности:

Шаг 1: Отметить те строки таблицы истинности, в которых формула принимает значение «ложь» (λ(F) = 0).

Шаг 2: Выписать для каждой отмеченной строки дизъюнкцию всех переменных следующим образом: если значение некоторой переменной в данной строке равно «ложь», то в дизъюнкцию включают саму эту переменную, иначе – ее отрицание.

Шаг 3: Все полученные дизъюнкции связать в конъюнкцию.

Она строится по следующим правилам:

– каждому нулю в таблице истинности сопоставляется дизъюнкция ранга n , где n –число аргументов функции; рангом дизъюнкции называют число аргументов, входящих в дизъюнкцию, причем в эту дизъюнкцию аргумент входит без инверсии, если в соответствующем наборе он принимает значение 0, и с инверсией, если принимает значение 1;

– все полученные дизъюнкции объединяются знаками конъюнкции.

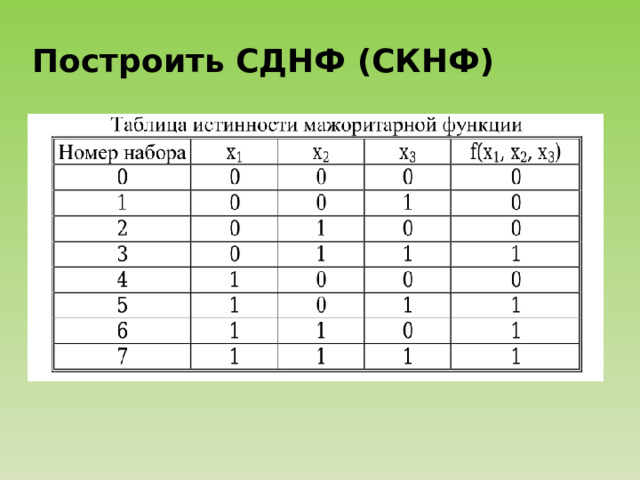
Построить СДНФ (СКНФ)

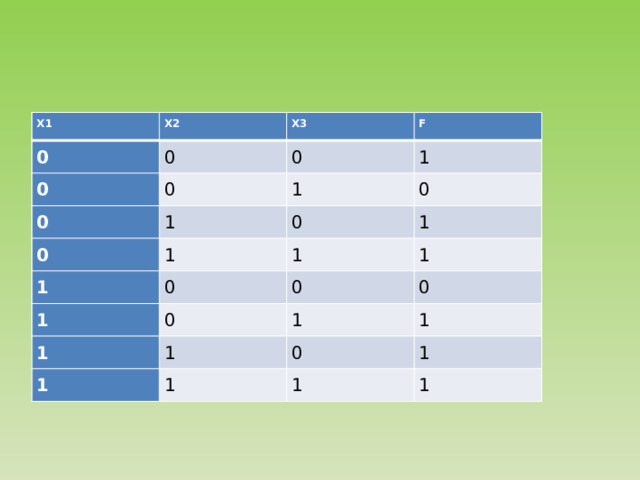
X1

X1

X2

0

0

X2

0

0

X3

0

0

X3

0

F

0

0

F

0

0

0

1

1

1

1

0

1

1

0

0

0

0

0

1

1

1

1

1

1

0

0

1

1

1

1

1

0

0

1

1

0

0

1

1

1

0

0

1

1

1

1

1

0

1

1

0

1

1

1

1

1

1

1

Минимизация булевых функций – представление булевых функций в самом экономичном коротком виде.

Дизъюнктивная нормальная форма называется минимальной, если она содержит наименьшее число вхождений переменных по сравнению со всеми равносильными ей ДНФ.

2. Упрощение булевых функций

Cвойства булевых функций

Идемпотентность

(Повторение)

Коммутативность (Переместительный закон)

Ассоциативность

(Сочетательный закон)

Законы поглощения

Дистрибутивность (Распределительный закон)

Свойства константы 1

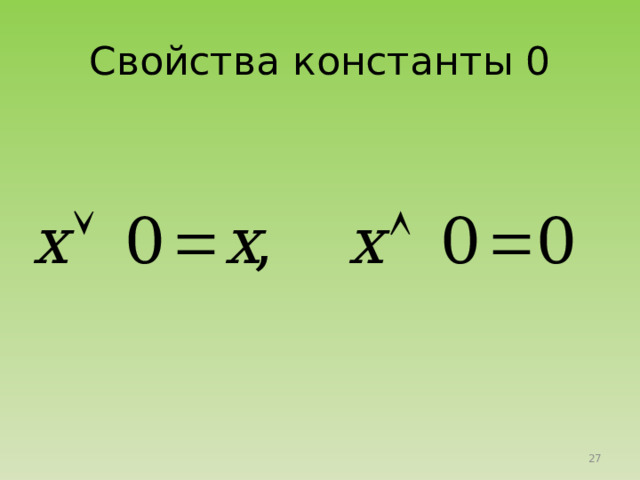
Свойства константы 0

Двойное отрицание

Закон де Моргана

Правило исключения третьего

(Закон непротиворечия)

Булевы функции n элементов

• Мажоритарная функция

1. Универсальные :

xV1 = 1;

xV 0 = х ;

х 1 = х ;

х 0 = 0.

Ассоциативность конъюнкции и дизъюнкции:

x ( yz ) = ( xy ) z ; xV ( y V z ) = ( x V y )V z .

Это свойство означает, что в конъюнкции или дизъюнкции нескольких переменных можно как угодно расставлять скобки (а значит, можно вообще их не ставить).

Поглощение (“целое поглощает часть”)

х V ху = х (1V у ) = х

Два распределительных закона

х ( yV z ) = x y V x z ;

хV ( y z) = ( xV y )( xV z )

оба свойства могут быть доказаны простым рассуждением (например, если х = 0, тогда по свойству 1 справа выражение равно 0 и слева тоже 0, если х = 1, то справа стоит y Ú z и слева будет то же самое)

Правила де Моргана

оба эти правила обобщаются на любое число переменных:

Правило Блейка

Пусть К 1 и К 2 – какие-то логические функции, тогда:

что легко доказывается справа налево :

Всякую формулу можно преобразовать так, что в ней не будет отрицаний сложных высказываний - все отрицания будут применяться только к простым высказываниям.

Замена эквиваленции и импликации на конъюнкцию, дизъюнкцию и отрицание.

Имеют место следующие равносильности:

 (1)

 (2)

Основные теоремы

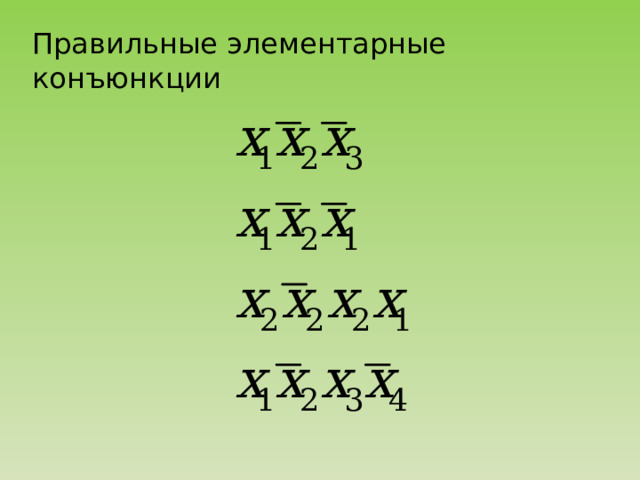
Правильные элементарные конъюнкции

Преобразовать до ДНФ

Задания

Докажите тождество

Преобразовать

Найти СДНФ

Найти СКНФ