Презентация занятия межшкольного факультатива по математике в 11 классах по теме Отработка навыков решения задания №7 ЕГЭ профильного уровня

I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

Отработка навыков решения задания №7 ЕГЭ профильного уровня.

«Мечтать – легко

и приятно, но думать трудно.

Умственный труд едва ли

не самый тяжёлый труд

для человека».

К.Д.Ушинский

Тема:

«Физический и геометрический смысл производной и касательная.

Применение производной к исследованию функций.»

Нужна ли производная в будущей профессии?

Решать задачи связанные с производной в наше время приходится представителям разных специальностей:

• Инженеры технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции;

• Конструкторы пытаются разработать прибор космического корабля так, чтобы масса прибора была наименьшей;

• Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными.

Составь пару

1

х

6

2

2х

11

3

7

a

1

Sinх

-3

4

8

16

12

2

cosx

-sinx

17

13

5

9

14

10

18

0

ax

15

19

20

Ответ.

Составь пару

1 -9

5 -

2 -

6 -

3 -

10 -

4 -

7 -

11 -

16 -

17 -

8 -

12 -

15 -

Ответ.

Составь пару

1 -9

5 -19

2 -4

6 -10

3 -5

10 -20

4 -19

7 -18

11 -14

16 -19

17 -13

8 -17

12 -19

15 -16

Вспомните!!!

• Каков физический смысл производной

функции?

2. Что является графиком линейной функции?

• Что называют угловым коэффициентом прямой?

• Каков геометрический смысл

производной функции?

• Какие промежутки называются

промежутками монотонности?

6. На каких промежутках функция возрастает?

Вспомните!!!

7.На каких промежутках функция

убывает?

8. Какая точка называется точкой максимума ?

9. Какая точка называется точкой минимума ?

10. Какие точки называются точками экстремума?

11. Когда точка х о является точкой максимума?

12. Когда точка х о является точкой минимума?

13. Необходимое условие экстремума?

Интересные и сторические факты

• Кто из учёных первым сформулировал геометрический смысл производной?

Готфрид Вильгельм Лейбниц - немецкий учёный математик и философ.

Интересные и сторические факты

о наибольшем и наименьшем значении.

• Латинские слова «maximum» u «minimum»

означают соответственно «наибольшее» и

«наименьшее» значение.

- Некоторыми вопросами отыскания наибольших и наименьших значений величин занимались ещё древнегреческие математики в III веке до н.э., например, Евклид и Архимед. Кеплер в 1615г,

Ферма в 1642 – 1644гг., голландец Гудде в 1658г,

Ньютон в 1671г, Лейбниц в 1684г, Эйлер в 1755г.

• Ньютон сформулировал так называемый принцип остановки: «Когда величина есть наибольшая или наименьшая из всех возможных, то она в этот момент не течёт ни вперёд, ни назад».

Отсюда он вывел своё правило: приравнять к нулю производную . Этим правилом мы и пользуемся.

Решения задач на физический смысл производной.

Задание 1. Материальная точка движется прямолинейно по закону  

(где  x - расстояние от точки отсчета в метрах,  t  — время в секундах, измеренное с начала движения).

В какой момент времени (в секундах) ее скорость была равна 2 м/с?

Решения задач на физический смысл производной.

Задание 1. Материальная точка движется прямолинейно по закону  

(где  x - расстояние от точки отсчета в метрах,  t  — время в секундах, измеренное с начала движения).

В какой момент времени (в секундах) ее скорость была равна

2 м/с?

Решение.

м/с.

Найдём закон изменения скорости: 

Чтобы найти, в какой момент времени  скорость была равна 2 м/с, решим уравнение:

с. 

Ответ: 7 .

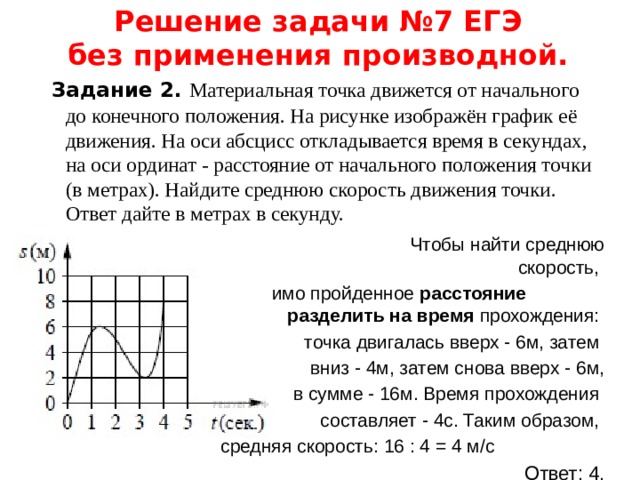
Решение задачи №7 ЕГЭ без применения производной.

Задание 2. Материальная точка движется от начального до конечного положения. На рисунке изображён график её движения. На оси абсцисс откладывается время в секундах, на оси ординат - расстояние от начального положения точки (в метрах). Найдите среднюю скорость движения точки. Ответ дайте в метрах в секунду.

Решение. Чтобы найти среднюю скорость,

необходимо пройденное расстояние разделить на время прохождения:

точка двигалась вверх - 6м, затем

вниз - 4м, затем снова вверх - 6м,

в сумме - 16м. Время прохождения

составляет - 4с. Таким образом,

средняя скорость: 16 : 4 = 4 м/с

Ответ: 4.

Решение устных задач на геометрический смысл производной и касательную.

• Задание 4.  На рисунке изображён график функции 

y=f(x)  и касательная к нему

в точке с абсциссой  x 0 .

Найдите значение

производной функции  f(x)  

в точке  x 0 .

Решение устных задач на геометрический смысл производной и касательную.

Задание 4.   Решение:

Значение производной в точке

касания равно угловому

коэффициенту касательной, который

в свою очередь равен тангенсу угла

наклона данной касательной

к оси абсцисс.

Построим треугольник с вершинами

в точках A (1; 2), B (1; −4), C(−2; −4).

Угол наклона касательной к оси

абсцисс будет равен углу  ACB :

Ответ: 2.

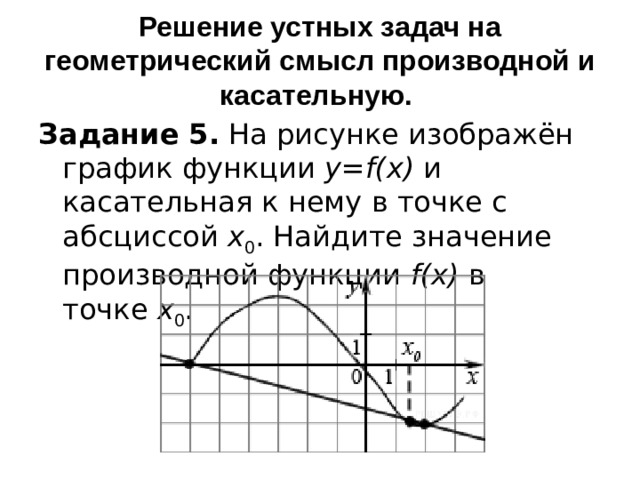
Решение устных задач на геометрический смысл производной и касательную.

Задание 5.  На рисунке изображён график функции  y=f(x)  и касательная к нему в точке с абсциссой  x 0 . Найдите значение производной функции f(x)  в точке  x 0 .

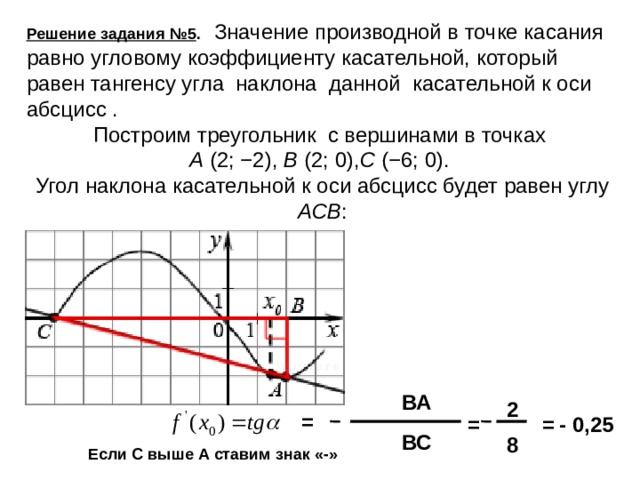
Решение задания №5 . Значение производной в точке касания равно угловому коэффициенту касательной, который равен тангенсу угла наклона данной касательной к оси абсцисс .

Построим треугольник с вершинами в точках 

A  (2; −2),  B  (2; 0), C  (−6; 0).

Угол наклона касательной к оси абсцисс будет равен углу ACB :

ВА

2

=

= - 0,25

=

ВС

8

Если С выше А ставим знак «-»

Задание №6. На рисунке изображён график функции                  и

касательная к нему в точке с абсциссой     .

Найдите значение производной функции           в точке     .

Если А ниже В

знак «+»

В

А

2

= 0,5

4

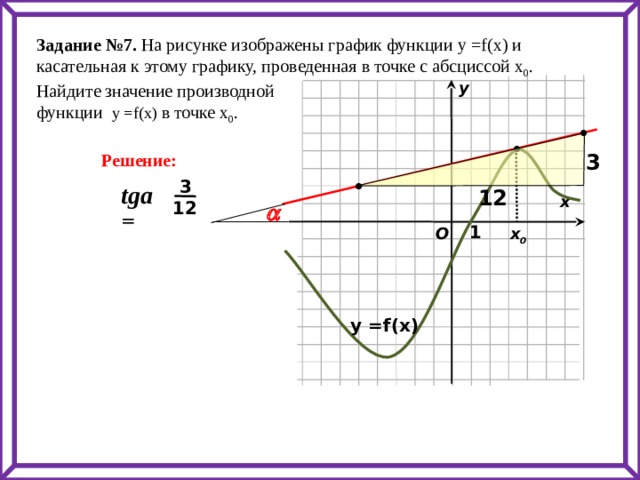
Задание №7. На рисунке изображены график функции у =f(x) и касательная к этому графику, проведенная в точке с абсциссой х 0 .

Найдите значение производной

функции у =f(x) в точке х 0 .

у

Решение:

3

3

tga =

12

х

12

a

a

1

х 0

O

у =f(x)

Решение задач на геометрический смысл производной и касательную.

Задание 8. На рисунке изображён график функции  y=f(x)  и касательная к нему в точке с абсциссой  x 0 . Найдите значение производной функции  f(x)

  в точке  x 0 .

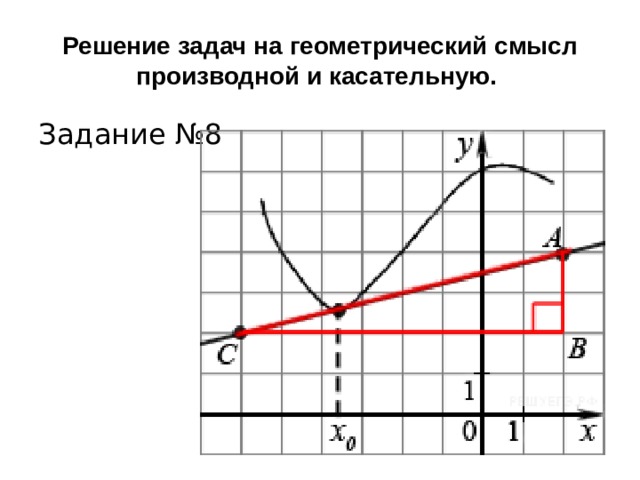
Решение задач на геометрический смысл производной и касательную.

Задание №8

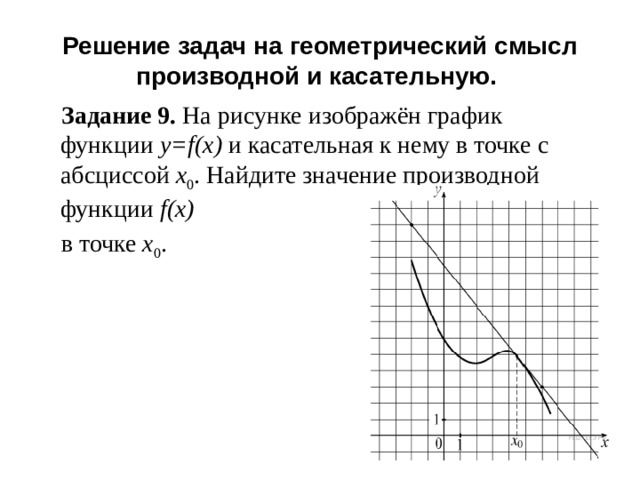
Решение задач на геометрический смысл производной и касательную.

Задание 9. На рисунке изображён график функции  y=f(x)  и касательная к нему в точке с абсциссой  x 0 . Найдите значение производной функции  f(x)

  в точке  x 0 .

Решение задач на геометрический смысл производной и касательную.

Задание №9

Решение задач на геометрический смысл производной и касательную.

Задание 10. На рисунке изображён график функции  y=f(x)  и касательная к нему в точке с абсциссой  x 0 . Найдите

значение производной

функции  f(x)  в точке  x 0 .

Решение устных задач на геометрический смысл производной и касательную.

Задание №10

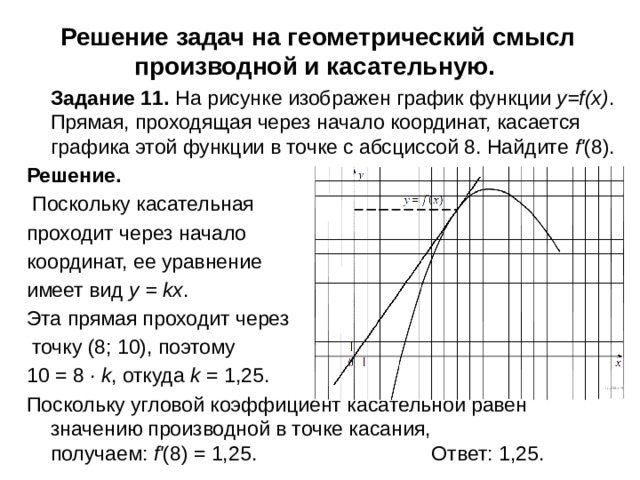
Решение задач на геометрический смысл производной и касательную.

Задание 11.  На рисунке изображен график функции  y=f(x) . Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите  f' (8).

Решение.

Поскольку касательная

проходит через начало

координат, ее уравнение

имеет вид  y = kx .

Эта прямая проходит через

точку (8; 10), поэтому

10 = 8 ·  k , откуда  k  = 1,25.

Поскольку угловой коэффициент касательной равен значению производной в точке касания, получаем:  f' (8) = 1,25. Ответ: 1,25.

Решение задач на геометрический смысл производной и касательную.

Задание 12. Прямая    является касательной к графику функции . Найдите абсциссу точки касания.

Решение. Условие касания графика функции    и прямой    задаётся системой требований:

В нашем случае имеем:

Проверка подстановкой показывает, что первый корень не удовлетворяет, а второй удовлетворяет уравнению (*). Поэтому искомая абсцисса точки касания −1.

Ответ: −1.

Задание 13. Прямая параллельна касательной к графику функции . Найдите абсциссу точки касания.

f’(x) = к

Две прямые параллельны или совпадают, тогда и только тогда, когда угловые коэффициенты равны.

Решение задач на геометрический смысл производной и касательную.

Задание 14. Прямая    параллельна касательной

к графику функции   .

Найдите абсциссу точки касания.

Решение задач на геометрический смысл производной и касательную.

Задание 15.

Прямая  y = 3 x  + 1 является касательной к графику функции  y = ax 2  + 2 x  + 3. Найдите  a .

Решение.

Прямая  является касательной к графику функции     в точке    тогда и только тогда, когда одновременно    и  .

Имеем:

Искомое значение  а  равно 0,125.

Ответ: 0,125.

Решение задач на геометрический смысл производной и касательную.

Задание 16. Прямая    является касательной к графику функции у = . Найдите  с .

Задание 17 . Прямая   является касательной к графику функции у = . Найдите  b, учитывая, что абсцисса точки касания больше 0.

Решение задач на применение производной к исследованию функций.

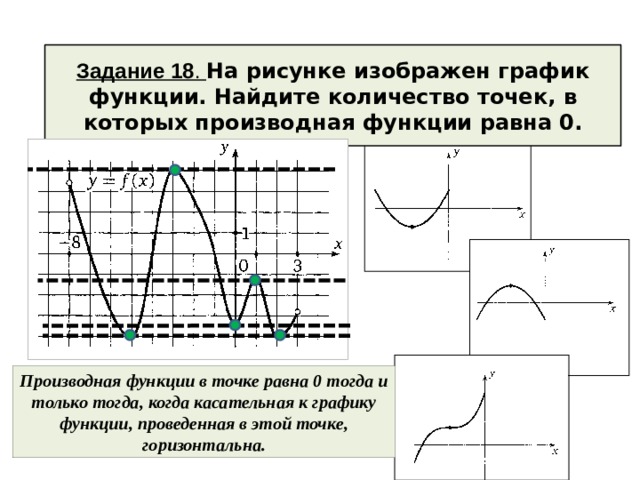
Задание 18 . На рисунке изображен график функции. Найдите количество точек, в которых производная функции равна 0.

Производная функции в точке равна 0 тогда и только тогда, когда касательная к графику функции, проведенная в этой точке, горизонтальна.

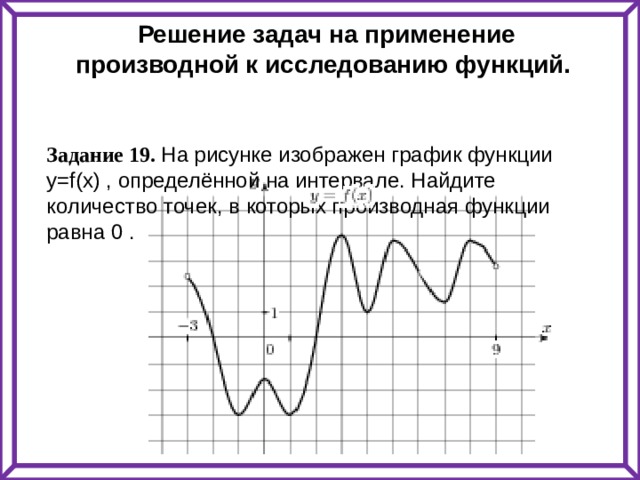
Решение задач на применение производной к исследованию функций.

Задание 19. На рисунке изображен график функции y=f(x) , определённой на интервале. Найдите количество точек, в которых производная функции равна 0 .

0, значит, функция возрастает. Найдем эти участки графика. Решение: 2. Найдем все целые точки на этих отрезках. y y = f (x) 5 4 3 2 1 x -9 -8 -7 -6 -5 - 4 -3 -2 -1 0 1 2 3 4 5 6 7 8 -1 -2 -3 -4 Ответ: 8 " width="640"

Задание 20. На рисунке изображен график функции у = f(x), определенной на интервале (-9; 8). Определите количество целых точек, в которых производная функции  положительна.

1. f / (x) 0, значит, функция возрастает. Найдем эти участки графика.

Решение:

2. Найдем все целые точки на этих отрезках.

y

y = f (x)

5

4

3

2

1

x

-9 -8 -7 -6 -5 - 4 -3 -2 -1

0 1 2 3 4 5 6 7 8

-1

-2

-3

-4

Ответ: 8

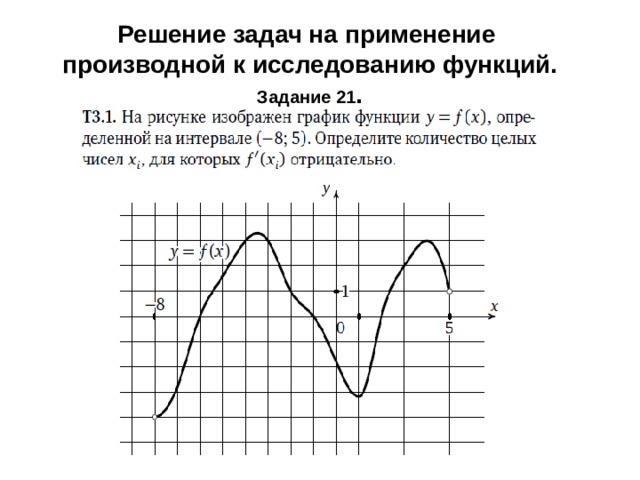
Решение задач на применение производной к исследованию функций.

Задание 21 .

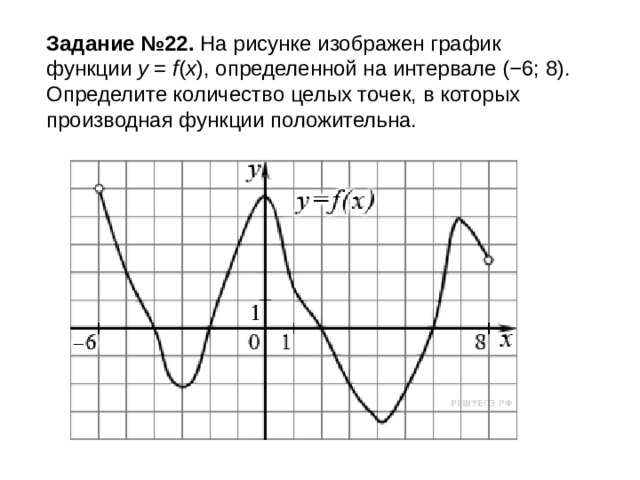
Задание №22.  На рисунке изображен график функции  y  =  f ( x ), определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.

Задание 22.  На рисунке изображён график функции    и восемь точек на оси абсцисс:  ,  ,  ,...,  . В скольких из этих точек производная функции    положительна ?

Задание 23

На рисунке изображен график производной функции. Найдите количество таких чисел , что касательная к графику в точке параллельна прямой y=3x-11 или совпадает с ней.

Две прямые параллельны или совпадают, тогда и только тогда, когда угловые коэффициенты равны.

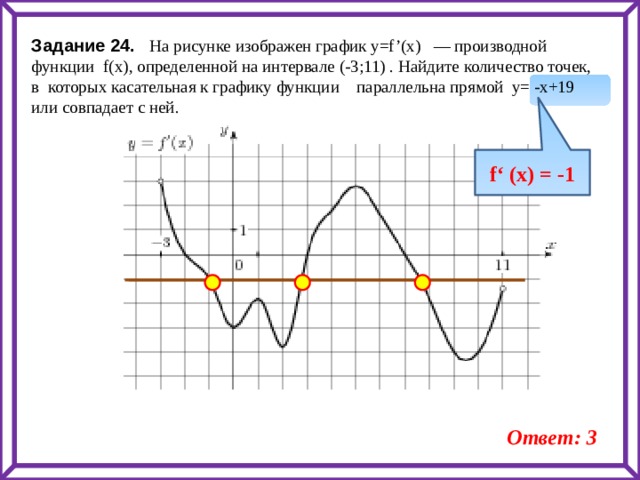
Задание 24. На рисунке изображен график y=f’(x)  — производной функции f(x), определенной на интервале (-3;11) . Найдите количество точек, в которых касательная к графику функции параллельна прямой y= -x+19 или совпадает с ней.

f‘ (x) = -1

Ответ: 3

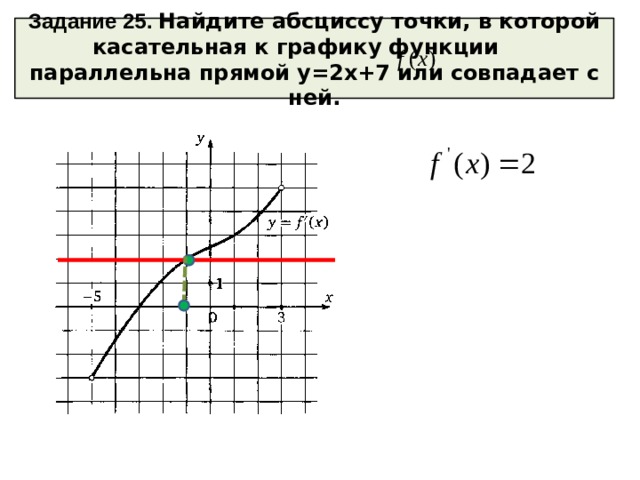
Задание 25. Найдите абсциссу точки, в которой касательная к графику функции параллельна прямой y=2x+7 или совпадает с ней.

Задание 26. На рисунке изображен график производной функции. Найдите промежутки убывания функции. В ответе укажите сумму целых чисел, входящих в эти промежутки .

Производная непрерывно дифференцируемой функции на промежутке убывания (возрастания) отрицательна (положительна)

-1 1 2 3 4 7

-1+0+1+2+3+4+7=16

Задание 27. На рисунке изображен график производной функции. Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек минимума.

y

y = f / (x)

4

3

2

1

4 точки экстремума

-7 -6 -5 -4 -3 -2 -1

x

1 2 3 4 5 6 7 8

-1

-2

-3

-4

-5

+

f / (x)

-8

–

8

–

+

+

x

6

3

0

-5

f(x)

Ответ:2

Задание 28. Найдите точку экстремума функции у =f (x) на отрезке [– 6; –1]

y

y = f / (x)

4

3

2

1

-7 -6 -5 -4 -3 -2 -1

x

1 2 3 4 5 6 7 8

-1

-2

-3

-4

-5

+

f / (x)

–

+

–

+

-8

8

x

6

3

0

-5

f(x)

Ответ:– 5

Задание 29. Найдите количество точек экстремума функции у =f (x)

на отрезке [– 3; 7]

y

y = f / (x)

4

3

2

1

-7 -6 -5 -4 -3 -2 -1

x

1 2 3 4 5 6 7 8

-1

-2

-3

-4

-5

+

f / (x)

8

-8

+

–

–

+

x

6

3

0

-5

f(x)

Ответ: 3

Задание 29. На рисунке изображен график y=f '(x)   — производной функции f(x) , определенной на интервале (-7;4) . Найдите точку экстремума функции f(x) , принадлежащую данному промежутку .

Ответ: -3

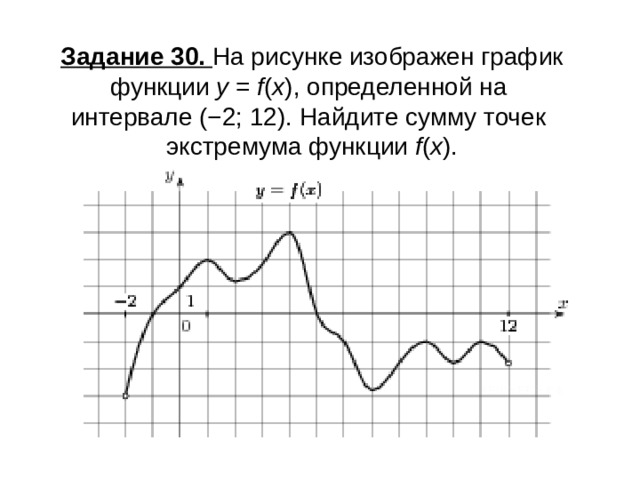
Задание 30. На рисунке изображен график функции  y  =  f ( x ), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции  f ( x ).

Задание 31.  На рисунке изображён график производной функции  f ( x ), определённой на интервале (−18; 6). Найдите количество точек минимума функции  f ( x ) на отрезке [−13;1].

Задание 32 .  На рисунке изображен график производной функции  f(x) , определенной на интервале (−7; 14). Найдите количество точек максимума функции  f(x)  на отрезке [−6; 9].

Задание 33. На рисунке изображен график y=f'(x)  — производной функции f(x) , определенной на интервале (-6;8) . Найдите промежутки возрастания функции f(x) . В ответе укажите длину наибольшего из них.

Ответ: 6

Задание 34. На рисунке изображен график y=f'(x) — производной функции f(x), определенной на интервале (-8;6). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.

Ответ: 3

Задание 35.   На рисунке изображен график производной функции  f(x) , определенной на интервале (−11; 3). Найдите промежутки возрастания функции  f(x) . В ответе укажите длину наибольшего из них.

Задание 36.  На рисунке изображен график производной функции  f(x) , определенной на интервале (−2; 12). Найдите промежутки убывания функции  f(x) . В ответе укажите длину наибольшего из них.

Задание 37. На рисунке изображен график y=f'(x)  - производной функции f(x) , определенной на интервале (-8:5). В какой точке отрезка [-3;2] функция принимает наибольшее значение?

у

х

Ответ:-3

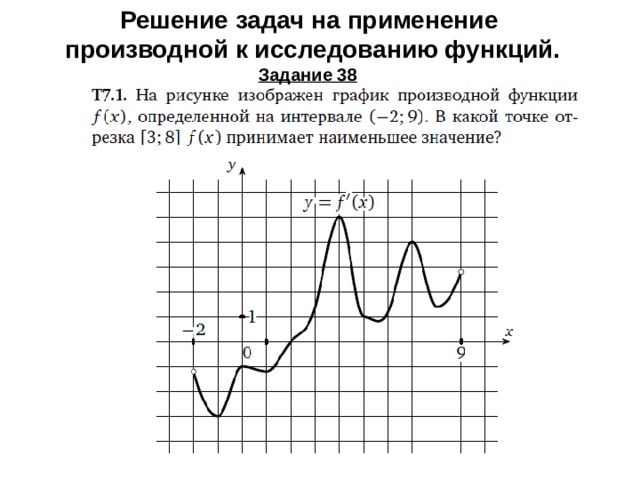
Решение задач на применение производной к исследованию функций. Задание 38

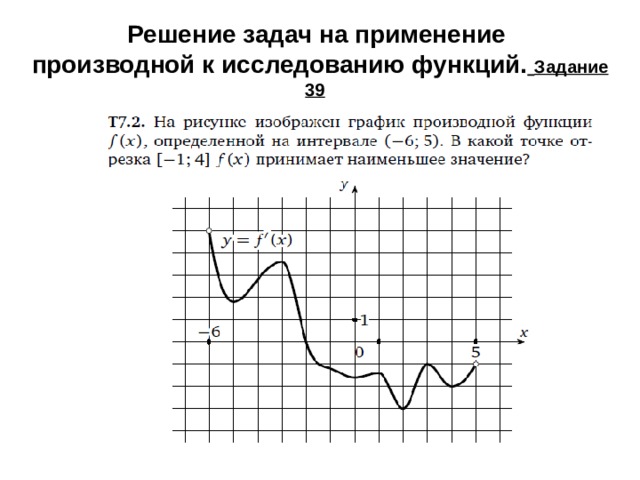
Решение задач на применение производной к исследованию функций. Задание 39

Решение задач на применение производной к исследованию функций. Задание 40

-4

Задание 41. На рисунке изображен график y=f‘(x) — производной функции f(x), определенной на интервале (-3;8) . Найдите промежутки возрастания функции. В ответе укажите сумму целых точек, входящих в эти промежутки.

-2

-1

0

1

2

6

7

-2+(-1)+0+1+2+6+7= 13

Ответ: 13

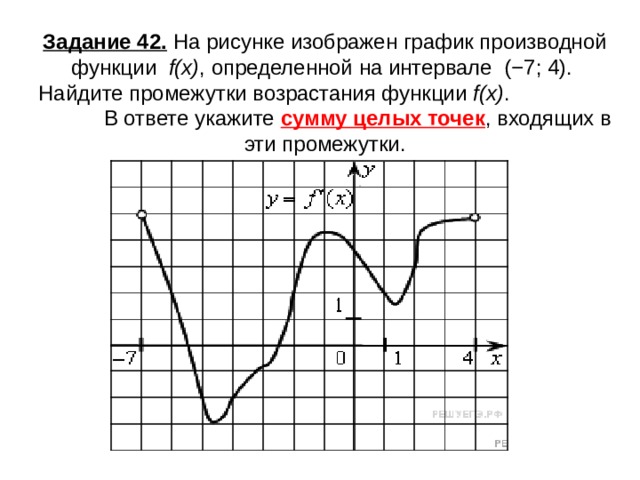
Задание 42.  На рисунке изображен график производной функции   f(x) , определенной на интервале (−7; 4). Найдите промежутки возрастания функции  f(x) . В ответе укажите сумму целых точек , входящих в эти промежутки.

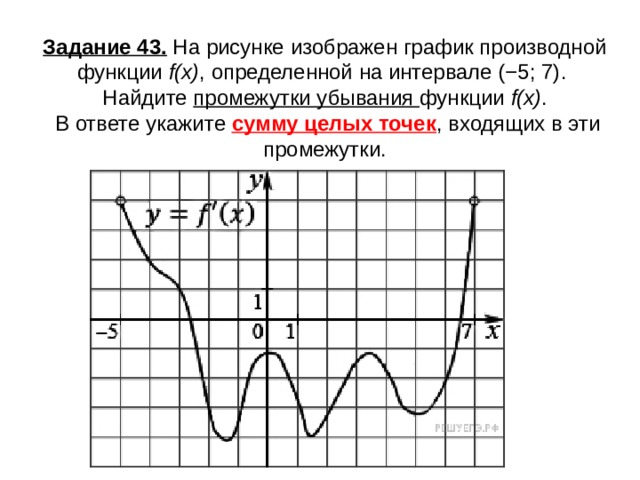
Задание 43.  На рисунке изображен график производной функции  f(x) , определенной на интервале (−5; 7). Найдите промежутки убывания функции  f(x) . В ответе укажите сумму целых точек , входящих в эти промежутки.

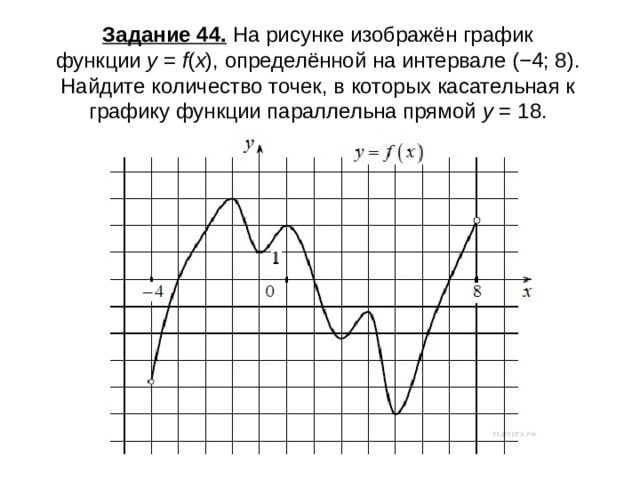
Задание 44.  На рисунке изображён график функции  y  =  f ( x ), определённой на интервале (−4; 8). Найдите количество точек, в которых касательная к графику функции параллельна прямой  y  = 18.

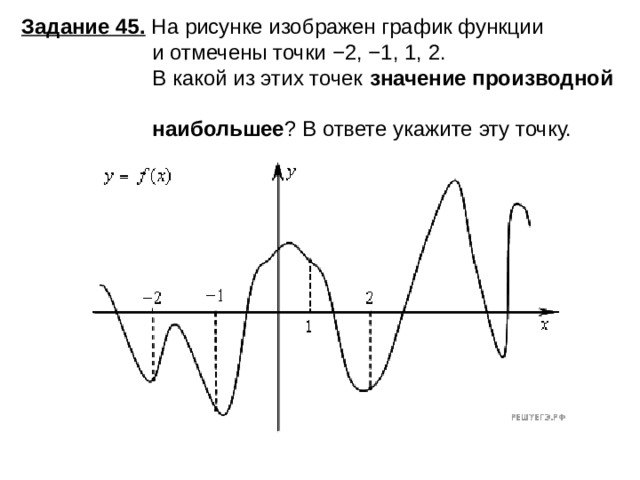
Задание 45.  На рисунке изображен график функции    и отмечены точки −2, −1, 1, 2. В какой из этих точек значение производной наибольшее ? В ответе укажите эту точку.

Самостоятельная работа по теме "Применение производной к исследованию функций. Геометрический смысл производной, касательная"

Ответы к самостоятельной работе

1

1вариант

2вариант

2

4

3

4,5

4

4

5

9

5

-24

0,75

6

2

0,25

7

2

-17

4

8

9

4

3

7

Домашнее задание

20 задач с одним рисунком

(задания №7 ЕГЭ профильного уровня)

Ну кто придумал эту математику !

Надо решить ещё пару примеров.

У меня всё получилось!!!

Материал с открытого банка заданий mathege.ru

Спасибо за работу!