Презентация "Четырехугольники.Подготовка к ОГЭ"

Четырёхугольники

Работу выполнила:

Пирожкова Марина Валентиновна ,

у читель математики

МОУ «Жилинская СОШ» (группа № 031)

Преподаватель:

Е.А. Никитин

Четырёхугольники

Справочник

Задачник

Проверь себя

Выход

Справочник

Четырёхугольники

Параллелограмм

Трапеция

Ромб

Прямоугольник

Квадрат

Четырёхугольник – это геометрическая фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков.

A

A

D

D

B

B

C

C

Параллелограмм – четырёхугольник, у которого противоположные стороны попарно параллельны

B

C

AB || CD

BC || AD

A

D

• Свойства параллелограмма
• Признаки параллелограмма
• Площадь параллелограмма
• Частные виды параллелограмма: прямоугольник и ромб

Свойства параллелограмма

• В параллелограмме противоположные стороны равны и противоположные углы равны.

2. Диагонали параллелограмма точкой пересечения делятся пополам.

C

B

AB = CD

BC = AD

A

D

B

C

A О = О C

B О = О D

О

D

A

Признаки параллелограмма

• Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
• Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм.

3. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.

B

C

BC || AD

BC = AD

A

D

B

C

BC = AD

А B = С D

A

D

C

B

A О = О C

B О = О D

О

A

D

Площадь параллелограмма

C

B

ВН – высота параллелограмма

AD - основание

A

S = BH ∙ AD

D

Н

B

C

S = AB ∙ AD ∙ sin α

α

A

D

Н

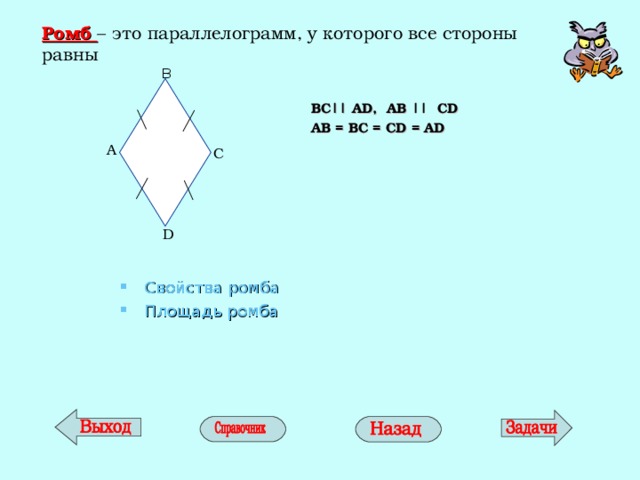
Ромб – это параллелограмм, у которого все стороны равны

B

BC|| AD , AB || CD

AB = BC = CD = AD

A

C

D

• Свойства ромба
• Площадь ромба

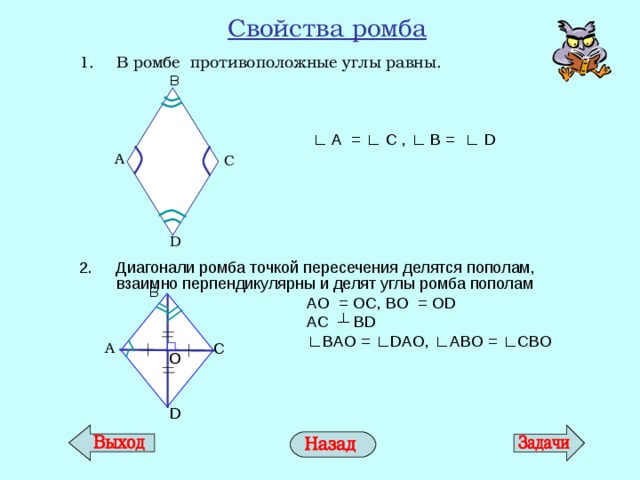
Свойства ромба

• В ромбе противоположные углы равны.

2. Диагонали ромба точкой пересечения делятся пополам, взаимно перпендикулярны и делят углы ромба пополам

B

∟ А = ∟ С , ∟ В = ∟ D

A

C

D

B

A О = О C , B О = О D

AC ┴ BD

∟ BAO = ∟ DAO, ∟ ABO = ∟ CBO

C

A

О

D

Площадь ромба

B

В

АН – высота ромба

D С - основание

А

C

A

С

O

S = А H ∙ D С

Н

D

D

В

S = 1/2∙ А C BD

α

S = АВ ∙ sin α

A

С

D

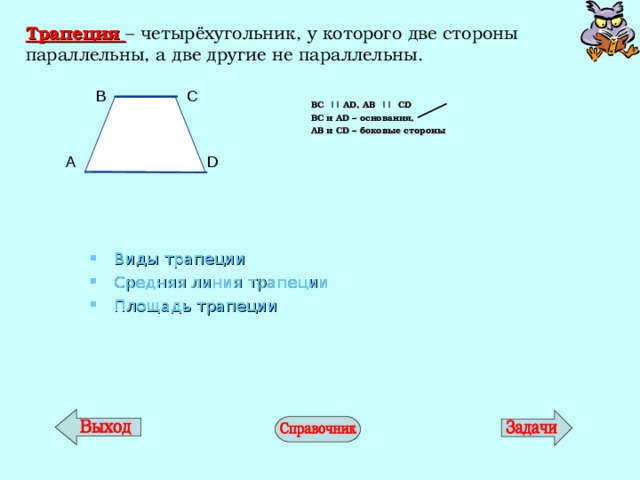
Трапеция – четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.

B

C

BC || AD , AB || CD

BC и AD – основания,

AB и CD – боковые стороны

A

D

• Виды трапеции
• Средняя линия трапеции
• Площадь трапеции

Виды трапеции

Равнобедренная - Прямоугольная - Произвольная

боковые стороны равны один из углов прямой

Средняя линия трапеции

C

B

Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон.

MN - средняя линия

М

N

A

D

Средняя линия трапеции параллельна основаниям и равна их полусумме

MN || AD , MN || AD ,

MN = ( BC + AD) / 2

Площадь трапеции

B

C

ВН – высота трапеции

ВС и AD - основания

D

A

H

S = 1/2 ∙ BH ∙ (ВС + AD )

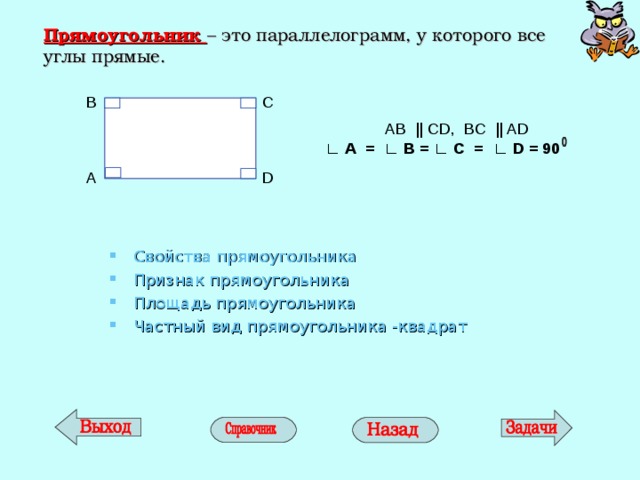
Прямоугольник – это параллелограмм, у которого все углы прямые.

С

В

AB || CD , BC || AD

∟ А = ∟ В = ∟ С = ∟ D = 90

A

D

• Свойства прямоугольника
• Признак прямоугольника
• Площадь прямоугольника
• Частный вид прямоугольника -квадрат

Свойства прямоугольника

• В прямоугольнике противоположные стороны равны и противоположные углы равны.

2. Диагонали прямоугольника равны и точкой пересечения делятся пополам.

B

C

AB = CD

BC = AD

A

D

C

B

BD = AC

A О = О C

B О = О D

О

D

A

Признак прямоугольника

C

B

BD = AC

О

D

A

Если в параллелограмме диагонали равны, то этот параллелограмм - прямоугольник

Площадь прямоугольника

С

В

A

D

S = А B ∙ AD

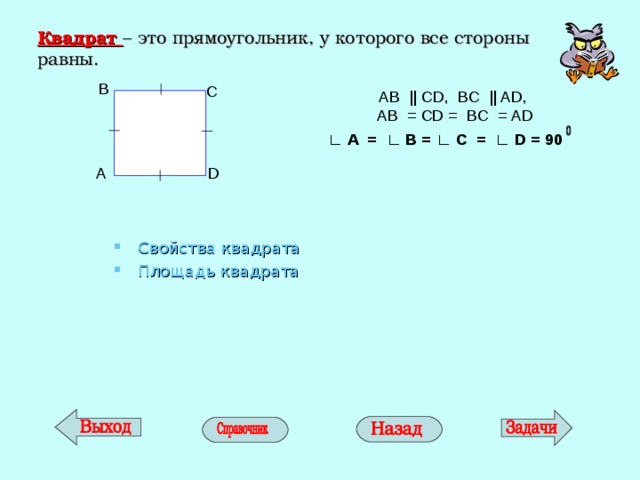
Квадрат – это прямоугольник, у которого все стороны равны.

В

С

AB || CD , BC || AD , ,

AB = CD = BC = AD

∟ А = ∟ В = ∟ С = ∟ D = 90

A

D

• Свойства квадрата
• Площадь квадрата

Свойства квадрата

• У квадрата все стороны равны и все углы равны.

2. Диагонали квадрата взаимно перпендикулярны, равны, точкой пересечения делятся пополам и делят углы квадрата пополам.

В

С

AB = CD = BC = AD

∟ А = ∟ В = ∟ С = ∟ D = 90

A

D

В

С

AC ┴ BD

BD = AC

A О = О C , B О = О D

∟ BAO = ∟ DAO, ∟ ABO = ∟ CBO

О

A

D

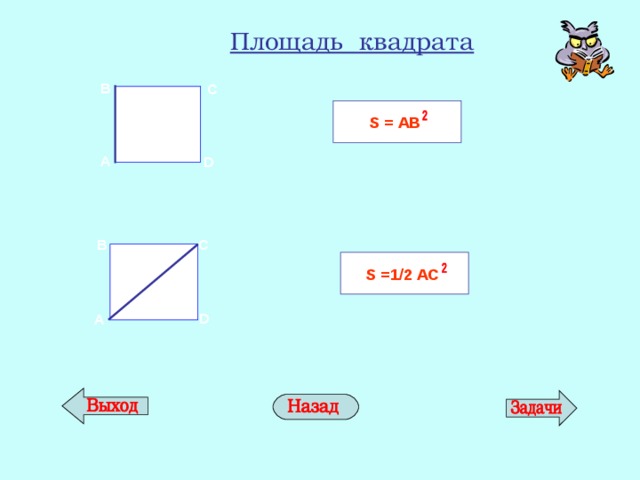
Площадь квадрата

В

С

S = АВ

А

D

В

С

S = 1/2 АС

D

А

задачник

Четырёхугольники

Параллелограмм

Трапеция

Ромб

Прямоугольник

Квадрат

Четырёхугольник

• Найдите углы выпуклого четырёхугольника, если они равны друг другу.
• Найдите углы выпуклого четырёхугольника, если они пропорциональны числам 1,2,4,5.
• Найдите стороны четырёхугольника, если его периметр равен 8 см, а одна сторона больше каждой из других сторон соответственно на 3 мм, 4мм и 5мм.
• Найдите стороны четырёхугольника, если его периметр равен 66 см, первая сторона больше второй на 8 см и на столько же меньше третьей стороны, а четвёртая в три раза больше второй.
• Докажите, что если не все углы выпуклого четырёхугольника равны друг другу, то хотя бы один из них тупой.

Параллелограмм

• Периметр параллелограмма равен 48 см. Найдите стороны параллелограмма, если разность двух сторон равна 7 см.
• Найдите углы параллелограмма, если сумма противолежащих углов равна 142.
• Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см.
• На диагонали BD параллелограмма ABCD отмечены точки P и Q так, что PB = QD . Докажите, что четырёхугольник APCQ – параллелограмм.
• В параллелограмме, смежные стороны которого не равны, проведены биссектрисы углов. Докажите, что при их пересечении образуется прямоугольник.

Ромб

• Найдите периметр ромба ABCD , в котором ∟ В = 60, АС= 10,5 см.
• Найдите углы ромба, если основание перпендикуляра, опущенного из вершины тупого угла, делит сторону ромба пополам.
• Найдите диагонали ромба, если одна из них в 1,5 раза больше другой, а площадь ромба равна 27 кв. см.
• Сторона ромба равна 24 см, а один из его углов 150 . Найдите расстояние между его противолежащими сторонами
• Из вершины В ромба ABCD , проведены перпендикуляры ВК и ВМ к прямым AD и DC . Докажите, что луч BD является биссектрисой ∟КВМ.

Прямоугольник

• Диагонали прямоугольника ABCD пересекаются в точке О. Докажите, что

треугольники АОВ и АО D равнобедренные.

• Биссектриса одного из углов прямоугольника делит большую сторону пополам. Найдите периметр прямоугольника, если его меньшая сторона 12 см.
• Стороны прямоугольника относятся как 2 : 7. Найдите стороны прямоугольника, если его площадь равна 108 кв.см.
• Сторона прямоугольника равна 4 см и образует с диагональю угол 60. Найдите эту диагональ.
• Пол комнаты, имеющий форму прямоугольника со сторонами 5,5 м и 6 м, нужно покрыть паркетом прямоугольной формы. Длина каждой дощечки паркета равна 30 см, а ширина – 5 см. Сколько потребуется таких дощечек для покрытия пола?

Квадрат

• Является ли четырёхугольник квадратом, если его диагонали:

а) равны и взаимно перпендикулярны;

б) взаимно перпендикулярны и имеют общую середину;

в) равны, взаимно перпендикулярны и имеют общую середину.

2. Диагональ квадрата 24 см. Найдите периметр четырёхугольника,

образованного отрезками, последовательно соединяющими

середины сторон данного квадрата.

• Сторону квадрата увеличили в 3 раза. Во сколько раз увеличилась его площадь?
• Площадь квадрата равна 18 кв.см. Найдите диагональ квадрата.
• В равнобедренный прямоугольный треугольник вписан квадрат так,

что две его вершины находятся на гипотенузе, а другие две – на катетах.

Найдите сторону квадрата, если известно, что гипотенуза равна 12 см.

Трапеция

• Найдите углы B и D трапеции ABCD с основаниями AD и BC , если ∟А = 36 ,∟С= 117 .
• Докажите, что трапеция равнобедренная, если её диагонали равны.
• Основания прямоугольной трапеции равны 10 см, 15 см, а один из углов – 45 .Найдите меньшую боковую сторону трапеции.
• Найдите площадь равнобедренной трапеции. Если её основания равны 16 см и 30 см, а диагонали взаимно перпендикулярны.
• Боковые стороны трапеции равны 13 см и 15 см, а периметр равен 48 см. Найдите среднюю линию трапеции

Проверь себя

Задание № 1

Какое из утверждений неверное:

• квадрат является одновременно параллелограммом и прямоугольником;
• угол между стороной и диагональю квадрата равен 45 ;
• существует квадрат, который не является ромбом;
• диагонали квадрата взаимно перпендикулярны.

Задание № 2

Найдите площадь ромба, диагонали которого равны 26 см и 8 см:

• 208 кв.см ;

• 104 кв.см;
• 52 кв.см;
• 68 кв.см

Задание № 3

В каком случае нельзя утверждать, что данная фигура – параллелограмм?

а) б)

в) г)

Задание № 4

Диагонали прямоугольника ABCD пересекаются в точке О. Определите периметр треугольника АВО, если АВ = 6 см, а диагональ прямоугольника равна 14 см:

• 19 см ;
• 26 см;
• 20 см;
• 18 см

Задание № 5

Какое из утверждений неверное?

• у прямоугольника углы прямые, а у ромба не обязательно;
• у ромба диагонали взаимно перпендикулярны, а у прямоугольника не обязательно;
• у ромба диагонали являются биссектрисами его углов, а у параллелограмма не обязательно;
• у ромба диагонали равны, а у прямоугольника не обязательно;

Задание № 6

Какая из фигур не является прямоугольником?

а) б)

в) г)

Задание № 7

В прямоугольнике ABCD проведена биссектриса АМ. ВМ= 5см,

МС =4 см. Найдите площадь прямоугольника:

• 36 кв. см
• 45 кв. см
• 28 кв. см
• 56 кв.см

Задание № 8

Найти площадь трапеции ABCD с основаниями AB и CD , если BC перпендикулярна AB , AB = 5 см, BC = 8 см, CD = 13 см.

• 144 кв.см;
• 36 кв.см;
• 72 кв.см;
• 70 кв.см

Задание № 9

Какое из утверждений неверное?

• параллелограмм, у которого диагонали взаимно перпендикулярны, является квадратом;
• прямоугольник, у которого все стороны равны, является квадратом;
• ромб у которого один угол прямой, является квадратом;
• ромб, у которого диагонали равны, является квадратом

Задание № 10

Найдите высоту параллелограмма, если его площадь

равна 75,6 кв. см, а основание - 14 см.

• 23,8 см ;
• 5,4 см;
• 61,6 см;
• 16 см.

Ещё!

Ещё!

Ending Style

Ending Style