Презентация для факультатива в 10кл.

Задачи к семинару по теме "Многогранники" 10кл.

Задачи к семинару по теме:  Многогранники.

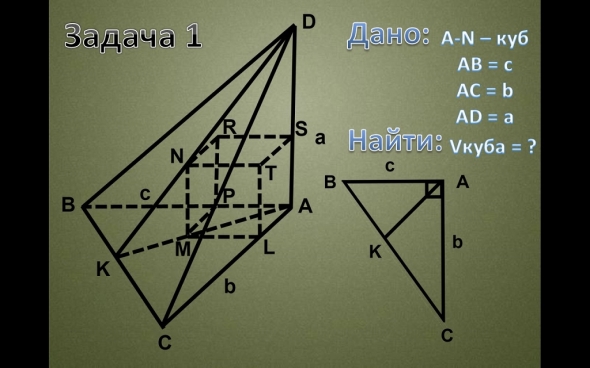
1.Рёбра треугольной пирамиды исходящие из вершины А попарно перпендикулярны, а их длины равны а; в и с. Найдите объём куба, вписанного в пирамиду так, что одна из его вершин совпадает с А.

2. Дана призма ABCDEFA₁B₁C₁D₁E₁F₁, в основании которой лежит правильный 6-угольник, а боковые рёбра наклонены к плоскости основания под углом 45°. Отрезок F₁A перпендикулярен (АВС). Найдите длину этого отрезка, если S бок.  призмы равна 50(1+Ö7).

3. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки Е, F - середины ребер соответственно SB и SC. Найдите косинус угла между прямыми АЕ и ВF.

4. Высота правильной призмы АВСАВС равна стороне её основания. На рёбрах ВВ₁ и А₁С₁ отмечены середины Д и Е соответственно. Найти S сечения (СДЕ), если АВ=а.

5. Боковое ребро SC пирамиды SАВC перпендикулярно плоскости основания (АВС). SC=а; ВС=2а; АС=а. Треугольник АВС-прямоугольный (С=90). М-середина SA. Найти S сечения, проходящего через точку С перпендикулярно ВМ.

6. Дана правильная четырехугольная пирамида SABCD.Боковое ребро SA=sqrt5, сторона основания равна 2.Найдиет расстояние от точки S до плоскости ADM, где M - середина ребра SC.

7. Угол между боковыми ребрами правильной четырехугольной пирамиды, не ле-

жащими в одной грани, равен 120°. Найдите плоский угол при вершине пирамиды.

8. Угол между боковыми ребрами правильной четырехугольной пирамиды, не ле-

жащими в одной грани, равен 120°. Найдите плоский угол при вершине пирамиды.

 9. Основание пирамиды DABC - равнобедренный треугольник АВС, в котором

AB = BC = 13, AC = 24. Ребро DB перпендикулярно плоскости основания и равно 20. Найдите тангенс двугранного угла при ребре АС.

 10. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите косинус угла между плоскостями АВС и BCS.

11. Точка E –середина ребра CC₁ куба ABCDA₁B₁C₁D₁. Найдите площадь сечения куба плоскостью A₁BE, если ребра куба равны 2.

12. В правильной четырехугольной призме ABCDA₁B₁C₁D₁ известно, что точка E лежит на ребре AA₁ так, что AE:A₁E=1:2. Найдите угол между плоскостями BD₁E и ABD, если сторона основания равна 2, а боковое ребро равно 3.

13. В правильной треугольной призме ABCA₁B₁C₁ все ребра которой равны 1, найдите расстояние между прямыми  AA₁ и BC₁ .

14. В правильной четырехугольной призме ABCDA₁B₁C₁D₁, стороны основания которого  равны 3, а боковые ребра равны 4, найдите угол между прямыми AC  и BC_1. 

15. В основании пирамиды лежит треугольник со сторонами 11, 24 и 31. Высота пирамиды равна 2. Все двугранные углы при ребрах основания равны. Найдите эти углы.

16. Дан куб ABCDA₁B₁C₁D₁ с ребром длиной . Найдите расстояние от середины ребра  B₁C₁ до прямой MT, где точки M и T- середины ребер  AD и A₁B₁.  

17. Найти площадь сечения куба ABCDA₁B₁C₁D₁ плоскостью, проходящей через вершину A и середину ребер C₁B₁ и С₁D₁, если сторона ребра равна 1.

18. Дан куб ABCDA'B'C'D' с ребром 5. Точка P лежит на A'D', так что A'P = 2. Найдите угол между плоскостью ABD и плоскостью PMB', где М - середина СС'.