Презентация "Функция"

ФУНКЦИЯ

y

0

х

1

1. Зависимость.

Множество А

Множество В

-элемент множества В.

-элемент множества А.

Зависимость между двумя множествами задана , если установлено правило , по которому элементам множества А ставятся в соответствие элементы множества В.

Зависимость

• Функция

• Произвольная

А

В

В

А

Каждому элементу множества А соответствует или ровно один или ни

одного элемента

множества B .

Каждому элементу множества А может соответствовать более одного элемента множества В.

2. Функция.

• Способы задания функции.

1.Описание.

Каждому целому числу соответствует его квадрат.

-5

-4

2.Таблица.

3.График .

25

…

16

4. Формула.

Y=3x+5 ;

у=х ² -4 x+9.

3

6

-5

0

8

-5

2

3

-1

0

y

b

x

a

0

Является ли данная линия графиком некоторой функции?

a)

y

Y 1

y

x 1

в)

0

x

у

у 2

б)

0

x

у 1

x

х 1

0

у 3

Исследование функций.

Пусть задана функция y = f(x) ,

где х - независимая переменная или аргумент,

Y – зависимая переменная или значение функции.

1.Область определения функции .

D(y) или D(f) -

Множество всех значений, которые может принимать переменная х

или все возможные

значения аргумента.

Пример:

1) y= 5x-7

D(y)=R ;

2) Y=√x

D(y)=[0 ; + ∞)

3) Y=1/(x-4)

D(y)=(- ∞ ;4) U (4; + ∞ )

или

D(y) : х ≠ 4.

0 х 0 " width="640"

2. Область значения функции

E(y) или E(f) -

Множество значений, которые может принимать зависимая переменная Y .

Примеры:

1) y = 2 - 5x

2) y = x²

3) y =-6/x

4) y = √x

E(y) = R

E(y) =[0 ; +∞)

E(y) = (- ∞ ; 0) U (0; +∞ )

E(y) =[0 ; +∞)

5) Найдите область определения и область значения функции у = 1 /x² , определите расположение графика этой функции в системе координат.

у

1) D(y)

: х ≠ 0

Ι

ΙΙ

2) E(y)

: у 0

х

0

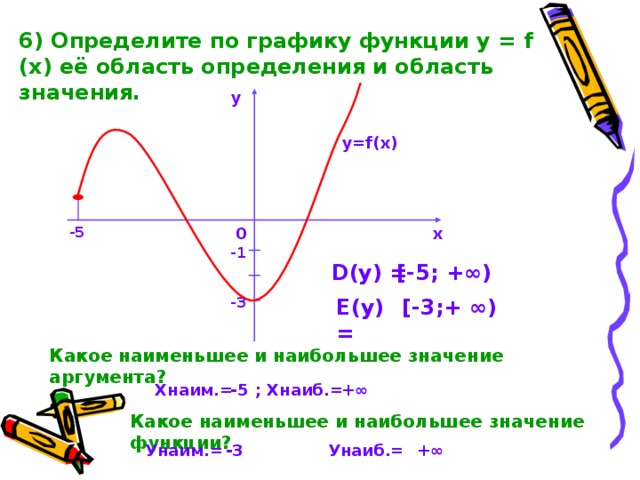
6) Определите по графику функции у = f (x) её область определения и область значения.

y

у= f(x)

-5

0

x

-1

D(y) =

[-5 ; +∞)

-3

E(y) =

[-3 ;+ ∞ )

Какое наименьшее и наибольшее значение аргумента?

Хнаим.= ; Хнаиб.=

-5

+∞

Какое наименьшее и наибольшее значение функции?

Унаим.= Унаиб.=

-3

+∞

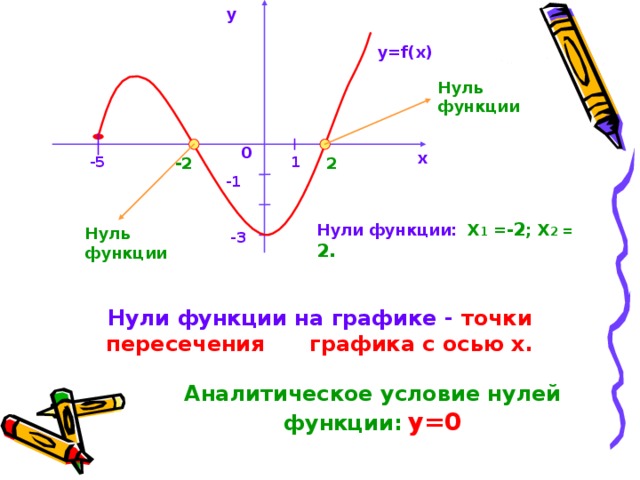
y

у= f(x)

Нуль функции

0

x

-5

1

2

-2

-1

Нули функции: Х 1 =- 2 ; Х 2 = 2.

Нуль функции

-3

Нули функции на графике - точки пересечения графика с осью х.

Аналитическое условие нулей функции: у=0

0 при x Є( X 1 ; X 2 ) U ( X 3 ; X 4 ) U ( X 5 ; +∞) Множества значений переменной х, при которых значения функции (у) либо положительные либо отрицательные, называется промежутками знакопостоянства данной функции. " width="640"

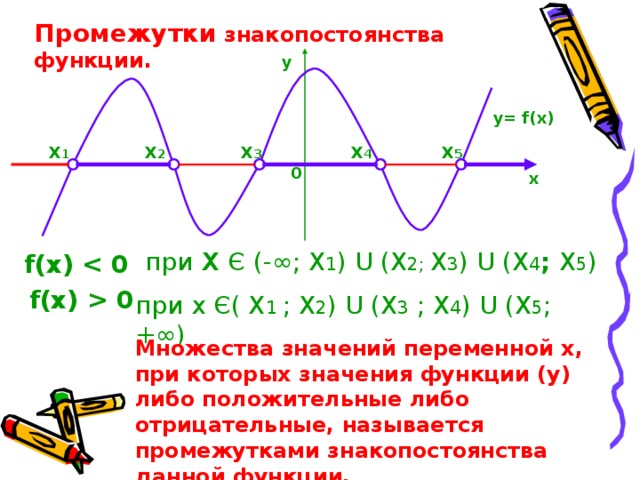
Промежутки знакопостоянства функции.

y

y= f(x)

X 4

X 5

X 3

X 1

X 2

0

x

при x Є (-∞ ; X 1 ) U ( X 2; X 3 ) U ( X 4 ; X 5 )

f(x)

f(x) 0

при x Є( X 1 ; X 2 ) U ( X 3 ; X 4 ) U ( X 5 ; +∞)

Множества значений переменной х, при которых значения функции (у) либо положительные либо отрицательные, называется промежутками знакопостоянства данной функции.

0 при х Є (-∞;0) U (2;+∞) f(x) при х Є (0;2) " width="640"

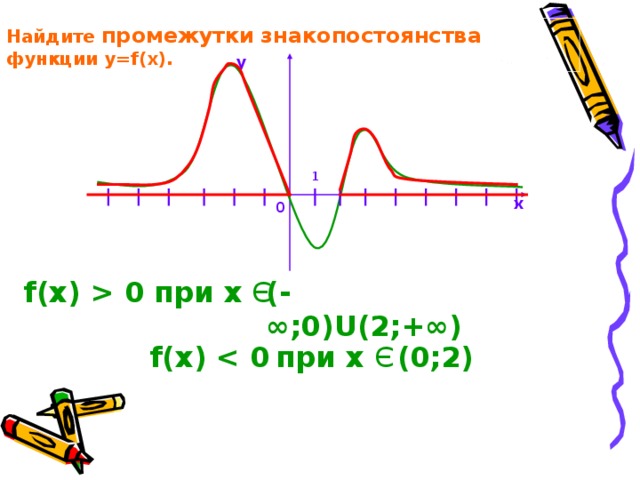
Найдите промежутки знакопостоянства функции y=f(x).

y

1

x

0

f(x) 0 при х Є

(-∞;0) U (2;+∞)

f(x) при х Є

(0;2)

0 при x Є (-5 ;2) U (6;+∞) y Y=f(x) x 6 0 -5 2 " width="640"

Изобразите график функции,

удовлетворяющий условиям:

f(x) 0 при x Є (-∞ ; -5) U (2;6)

f(x) 0 при x Є (-5 ;2) U (6;+∞)

y

Y=f(x)

x

6

0

-5

2

Промежутки возрастания и убывания функции.

у

У 2

У 1

0

а

х

Х 1

Х 2

У= f(x)

У1 У2

Х 2 Є (-∞; а ]

Х 1 Х 2

Х 1 Є (-∞; а ] ;

На промежутке (-∞; а ] большему значению х соответствует большее значение у

или большему значению аргумента соответствует большее значение функции.

Функция

возрастает на промежутке (-∞; а ]

У4. На промежутке [ а; +∞) меньшему значению х соответствует большее значение у или меньшему значению аргумента соответствует большее значение функции. Функция убывает на промежутке [ а; +∞). " width="640"

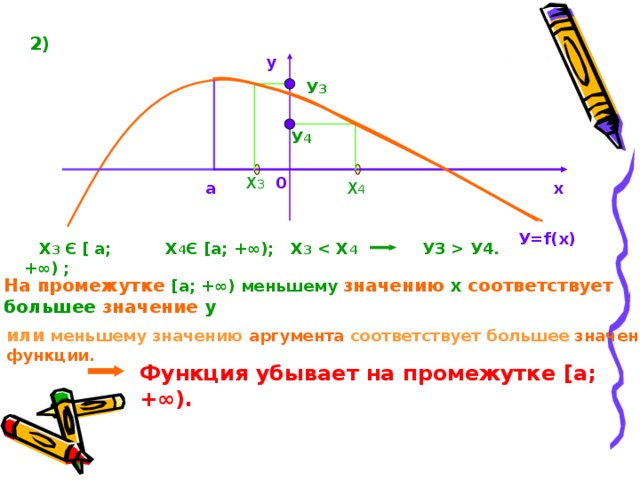
2)

у

У 3

У 4

0

Х 3

х

Х 4

а

У= f(x)

Х 4 Є [ а; +∞);

Х 3 Х 4

Х 3 Є [ а; +∞) ;

У3 У4.

На промежутке [ а; +∞) меньшему значению х соответствует большее значение у

или меньшему значению аргумента соответствует большее значение функции.

Функция убывает на промежутке [ а; +∞).

Определите по графику функции y=f(x) промежутки возрастания и убывания функции.

у

-8

0

х

-4

-10

5

[ 0;5 ]

Функция y = f (x) убывает на (-∞;-8 ] ;

[ 5;+∞)

Функция y = f(x) возрастает на [ -8;0 ] ;

Функция y = f(x) имеет и промежутки возрастания и промежутки убывания

является

немонотонной функцией.

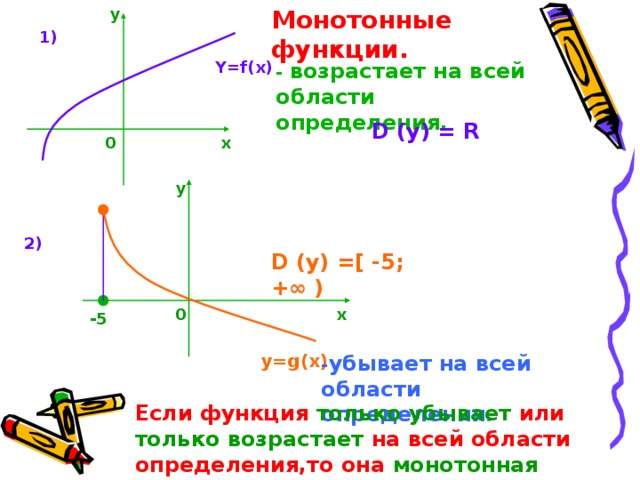
Монотонные функции.

у

1)

Y=f(x)

- возрастает на всей области определения.

D (y) = R

х

0

у

2)

D (y) =[ -5 ; +∞ )

х

0

-5

y=g(x)

- убывает на всей области определения .

Если функция только убывает или только возрастает на всей области определения,то она монотонная функция .

y

Точки экстремума.

Y 0

Функция y=f(x) возрастает на ( - ∞; Х 0 ]

Функция y=f(x) убывает на [ Х 0 ;+∞ )

x

0

X 0

Y=f (x)

Точка Х 0 -точка экстремума,

т.к. в этой точке промежуток возрастания меняется на промежуток убывания,

т.е.в точке Х 0 меняется характер монотонности функции y=f(x) .

f (х)

х

Х 0

X 0 - точка максимума.

Х m ах = Х 0

Y 0 – значение функции в точке максимума.

Y max = Y 0

Y 0 – экстремум функции у = f (x) .

у

Y= f(x)

X 1

0

х

Функция Y= f(x) убывает на (-∞; X 1 ]

Функция Y= f(x) возрастает на [ Х 1 ;+∞)

У 1

В точке Х 1 функция меняет характер монотонности от убывания к возрастанию,

Х 1 – точка экстремума.

f(x)

х

Х 1

Х 1 - точка минимума ,

Х min = Х 1

У 1 – значение функции Y= f(x) в точке минимума,

У min = Y 1 .

У 1 – экстремум функции .

0; у 0) 5.Промежутки возрастания и убывания функции. 6.Точки экстремума. 7. Экстремумы функции. -2 [ -2 ; 5 ] Х = 0; Х = 2. У 0 при Х Є (-∞;0) U (2;+ ∞); У 0 при Х Є (0 ; 2) f(x) возр. на (-∞;-2 ] ; [ 1;3 ] , f(x) убыв. на [ -2; 1 ] ; [ 3 ;+∞) Х min=1 . Х max =-2 ; У min = -2 . У max = 3 ; У max =5 ; Х max =3 ; " width="640"

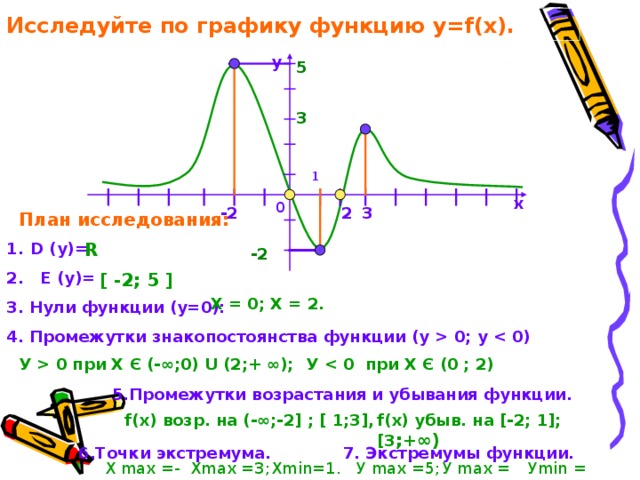
Исследуйте по графику функцию y=f(x).

y

5

3

1

x

0

2

3

-2

План исследования:

• D (y)=

R

2. E (y)=

3. Нули функции (у=0):

4. Промежутки знакопостоянства функции (у 0; у 0)

5.Промежутки возрастания и убывания функции.

6.Точки экстремума. 7. Экстремумы функции.

-2

[ -2 ; 5 ]

Х = 0; Х = 2.

У 0 при Х Є (-∞;0) U (2;+ ∞);

У 0 при Х Є (0 ; 2)

f(x) возр. на (-∞;-2 ] ; [ 1;3 ] ,

f(x) убыв. на [ -2; 1 ] ; [ 3 ;+∞)

Х min=1 .

Х max =-2 ;

У min = -2 .

У max = 3 ;

У max =5 ;

Х max =3 ;

Проведите исследование функции по графику:

у

1

0

х

1

У = f (x)