Презентация "И в танце есть математический расчет"

И В ТАНЦЕ ЕСТЬ МАТЕМАТИЧЕСКИЙ РАСЧЁТ

Выполнила ученица 7 «а»

Ушакова Александра

Руководитель:

Морозова С.В.

«Чем дольше живет математика, тем более абстрактной и, возможно, как раз, поэтому тем более практичной она становится. »

Эрик Темпл Белл

Цель работы:

• выявить математическую составляющую в танце

Задачи:

• проанализировать литературу по данной теме ;
• изучить танец планет и пчёл с точки зрения математики;
• выявить математический расчёт в современном танце.

Танец пчёл

Виды танцев:

• круговые
• виляющие

Круговой танец

Исполняется в том случае, когда источник питания находится менее, чем в 100 метрах от улья

Виляющий танец пчёл

• Исполняется, когда расстояние до источника питания более 100 метров

От летка до медоноса

• Пчелы, окружающие танцовщицу, запоминают угол между направлением на цель, показанным у летка, и солнцем на небе и летят за взятком, сохраняя этот угол.

Танец планет

• Планеты в небе двигаются в изящных орбитальных моделях, танцуя под музыку космоса. В этих движениях существует больше математической и геометрической гармонии, чем мы думаем.

Уникальный ритм танца планет

• Поскольку планета, двигающаяся по внутренней орбите, двигается более быстро, чем двигающаяся по внешней орбите, то образуются интересные модели.
• Каждая планетарная пара имеет свой собственный уникальный ритм танца.

Танец Земли и Венеры

Земля:

8 лет * 365.256 дней

в году = 2 922.05 дня

Венера:

13 лет * 224.701 дня в году = 2921.11 дня

(то есть 99.9 %)

• Наблюдая за танцем Земли и Венеры в течение восьми лет создается этот красивый цветок с пятью лепестками и Солнцем в центре.

Танец

Марса и Венеры

Марса и Земли

Танец

Сатурна и

Юпитера

Юпитера и Земли

Танец

Земли и Меркурия

Урана и Сатурна

Современные танцы

• Танец – искусство пластических и ритмических движений тела.
• Движения - это изменение плоскости, при котором сохраняются размеры и форма объектов.

Симметрия в математике

1) Осевая симметрия

Две точки А и А 1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА 1 и перпендикулярна к нему.

2) Центральная симметрия

АА 1 а, АО = ОА 1

Две точки А и A 1 называются симметричными относительно точки О, если О – середина отрезка АА 1 .

3) Зеркальная симметрия

AO=A 1 O

Отображение пространства на себя, при котором любая точка Р переходит в симметричную ей относительно этой плоскости  точку Р 1 .

Симметрия в танце

1) Симметрия балетных позиций ног, рук, тела, головы

2) Симметрия рисунка танца

(формирование на сцене однородной структуры в линии и рисунки - круг, клин, квадрат и др.)

3) Симметрия исполняемых движений

Параллельность прямых и плоскостей

1) Параллельность прямых на плоскости

2) Параллельность прямых в пространстве

3) Параллельность прямой и плоскости

4) Параллельность плоскостей

Параллельность в танце

1) Параллельность позиций

2) Параллельность партнёров

3) Параллельность полу

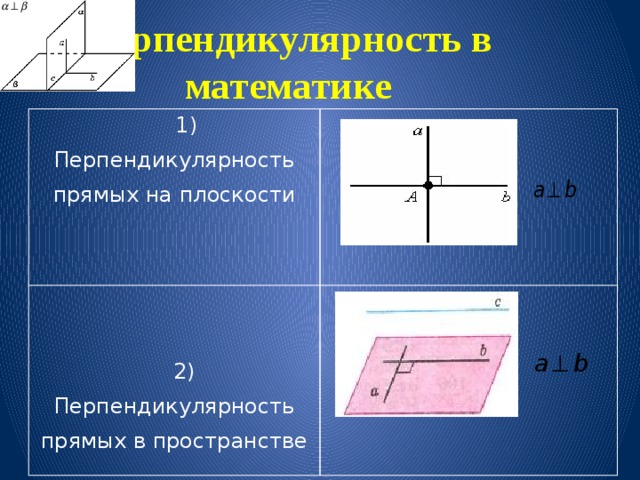
Перпендикулярность в математике

  1) Перпендикулярность прямых на плоскости

2) Перпендикулярность прямых в пространстве

3) Перпендикулярность прямой плоскости

4) Перпендикулярность плоскостей

Перпендикулярность в танце

1) Перпендикулярность полу

Элемент танца, при котором

2) Перпендикулярность частей тела

какая-либо часть тела перпендикулярна

Элемент танца, при котором части тела перпендикулярны друг другу

полу.

(например, гранд батман 8 ).

Основные геометрические

понятия в танце

Прямая (линия)

Точка (точка опоры)

Угол

Батман тандю 30 °

Батман жете 45 °

Батман девлопэ 90 °

Арабеск

120 °

Окружность

1) В рисунке танца

2) В позициях рук

3) В классическом экзерсисе

4) В движениях

Равновесие и баланс

Устойчивые фигуры

Неустойчивые фигуры

Графики функций в танце

Вывод:

• После исследования вышеперечисленных танцев я убедилась, что и в танцах несомненно есть математический расчёт .

Красота есть первое требование: в мире нет места некрасивой математике, ровно как и не найдется места некрасивому танцу.