Презентация к уроку: "Электромагнитные колебания", 11 класс.

Переменный электрический ток

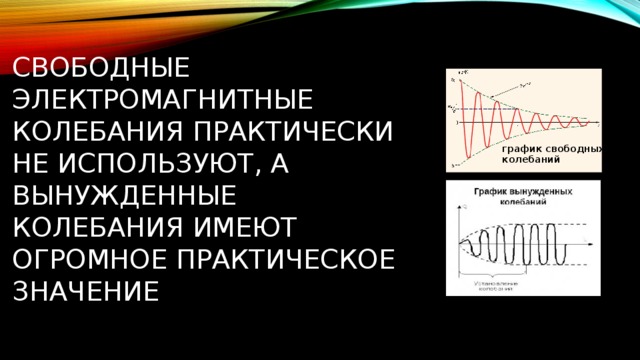
Свободные электромагнитные колебания практически не используют, а вынужденные колебания имеют огромное практическое значение

график свободных колебаний

Переменный электрический ток представляет собой вынужденные электромагнитные колебания

Под переменным током также подразумевают ток в обычных одно- и трёхфазных сетях. В этом случае мгновенные значения тока и напряжения изменяются по гармоническому закону.

примитивная установка для выработки переменного тока.

Осциллограф -

прибор, предназначенный для исследования (наблюдения, записи, измерения) амплитудных и временных параметров электрического сигнала, подаваемого на его вход, либо непосредственно на экране, либо записываемого на фотоленте

Проволочную рамку, вращающуюся в постоянном однородном магнитном поле, можно рассматривать как простейшую модель генератора переменного тока. Поток магнитной индукции Ф , пронизывающий проволочную рамку площадью S , пропорционален косинусу угла а между нормалью к рамке и вектором магнитной индукции:

Ф = BScos а

Вынужденные электрические колебания – это колебания, происходящие в цепях под действием напряжения, меняющегося с циклической частотой по закону синуса или косинуса

U m -амплитуда напряжения

Если напряжение меняется с циклической частотой , то и сила тока в цепи будет меняться с той же частотой. Но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае сила тока і определяется по формуле:

Активное сопротивление.

Действующие значения

силы тока и напряжения.

Сопротивление, включенное в цепь переменного тока, в котором происходит превращение электрической энергии в полезную работу

или в тепловую энергию, называется активным сопротивлением .

Мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому для нахождения мгновенного значения силы тока можно применить закон Ома

i=u/R=U m cos ωt/R = I m cos ωt

В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряжения, а амплитуда силы тока определяется равенством

I m = U m / R

• Мощность в цепи постоянного тока на участке с сопротивлением R определяется по формуле

• Мгновенная мощность в цепи переменного тока на участке с активным сопротивлением R, определяется формулой

• Средняя мощность равна

P=I 2 R

P=i 2 R

P ¯= i 2 R = I 2 R/2

Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы переменного тока. Действующее значение силы переменного тока обозначается через I:

Действующее значение переменного напряжения определяется аналогично действующему значению силы тока:

Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.

КАТУШКА ИНДУКТИВНОСТИ В ЦЕПИ ПЕРЕМЕННОГО ТОКА

Индуктивность в цепи влияет на силу переменного тока. Это можно доказать с помощью простого опыта.

Соберем цепь из катушки с большой индуктивностью и электрической лампы накаливания (рис. 4.16). С помощью переключателя можно подключить эту цепь либо к источнику постоянного напряжения, либо к источнику переменного напряжения. При этом постоянное напряжение и действующее значение переменного напряжения должны быть равны.

Опыт показывает, что лампа светится ярче при постоянном напряжении. Следовательно, действующее значение силы переменного тока в рассматриваемой цепи меньше силы постоянного

Объясняется это различие явлением самоиндукции.

Если напряжение быстро меняется, то сила тока не будет успевать достигнуть тех значений, которые она приобрела бы с течением времени при постоянном напряжении.

Следовательно, максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения .

i

- k

=

Из равенства

Определим силу тока в цепи, содержащей катушку, активным сопротивлением которой можно пренебречь (рис. 4.17). Для этого предварительно найдем связь между напряжением на катушке и ЭДС самоиндукции в ней.

следует, что удельная работа вихревого поля (т. е. ЭДС самоиндукции е і ) равна по модулю и противоположна по знаку удельной работе кулоновского поля. Учитывая, что удельная работа кулоновского поля равна напряжению на концах катушки, можно записать: е і = -u.

Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна быть равна нулю. Иначе сила тока, согласно закону Ома, была бы бесконечно большой. Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля

При изменении силы тока по гармоническому закону :

i =  I m   sin

t

ЭДС самоиндукции равна

l m cos

e і = - L i ' = - L

t.

порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля

Так как u = -е і , то напряжение на концах катушки оказывается равным

создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.

Следовательно, колебания напряжения на катушке опережают по фазе колебания силы тока на

Индуктивное сопротивление зависит от частоты

Постоянный ток вообще «не замечает» индуктивности катушки. При = 0

индуктивное сопротивление равно нулю (X L = 0).

или, что то же самое, колебания силы тока отстают по фазе от колебаний напряжения на (рис. 4.18)

Чем быстрее меняется напряжение, тем больше ЭДС самоиндукции и тем меньше амплитуда силы тока.

Амплитуда силы тока в катушке равна:

Катушка индуктивности оказывает сопротивление переменному току.

Это сопротивление, называемое индуктивным, равно произведению циклической частоты на индуктивность

и вместо амплитуд силы тока и напряжения использовать их действующие значения, то получим:

Колебания силы тока в цепи с индуктивностью отстают по фазе от колебаний напряжения на

Величину X L , равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.

Согласно формуле (4.35) действующее значение силы тока связано с действующим значением напряжения и индуктивным сопротивлением соотношением, подобным закону Ома для цепи постоянного тока.

Резонанс в электрической цепи

Мы рассмотрим что же такое резонанс в электрической цепи

Резонанс

Резонанс в электрической цепи это Резонанс в электрической цепи — явление резкого возрастания амплитуды ​вынужденных колебаний тока при приближении частоты внешнего ​напряжения (эдс) и собственной частоты колебательного контура.

Резонанс в электрическом колебательном контуре

резонанс токов возникает при параллельном соединении емкости и катушки, когда проводимости ветвей равны, а резонанс напряжений - когда равны напряжения на реактивных элементах, соединенных последовательно

Пример резонанса