Презентация к уроку геометрии по теме : "Призма". Вводный урок. 10 класс.

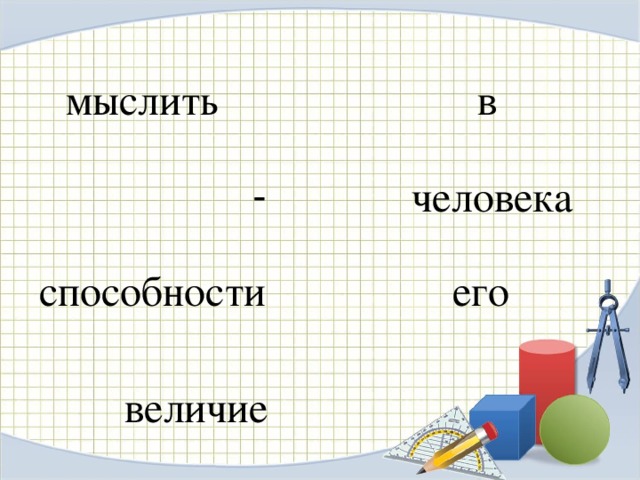
мыслить

в

человека

-

его

способности

величие

«Величие человека – в его способности мыслить».

квадрат

Игра крестики – нолики.

1

2

3

4

5

• Треугольник равносторонний, если равны все его углы.

2. У ромба диагонали пересекаются под прямым углом

3. У равнобедренного треугольника все стороны равны

4. Сумма углов любого четырехугольника равна 180 ◦ .

5. Площадь трапеции равна произведению суммы его оснований на высоту.

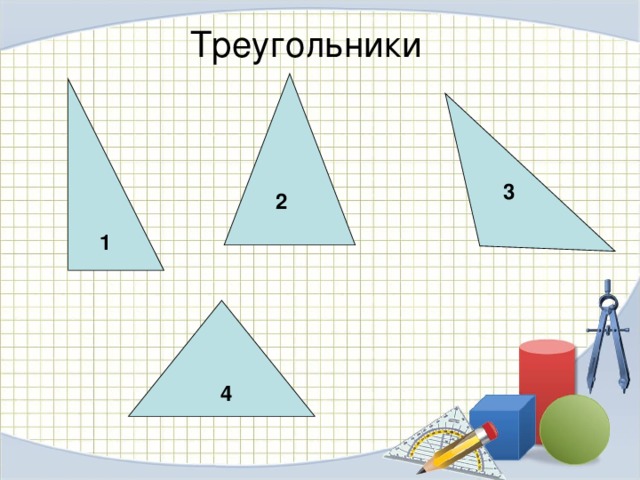
Треугольники

3

2

1

4

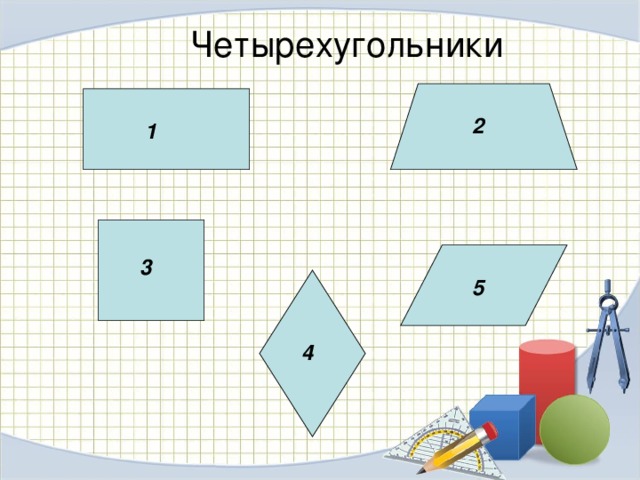
Четырехугольники

2

1

3

5

4

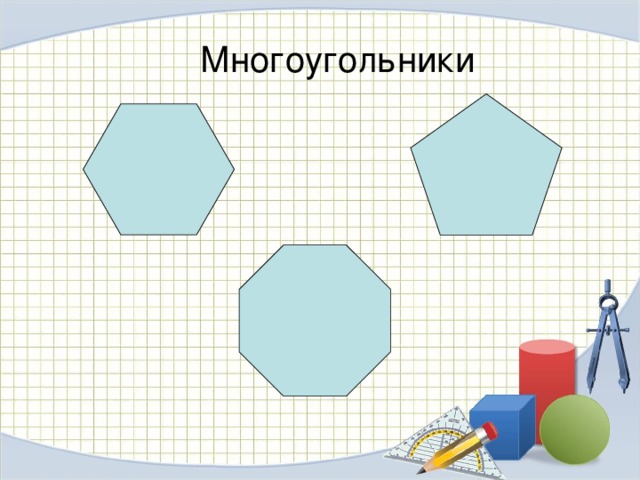
Многоугольники

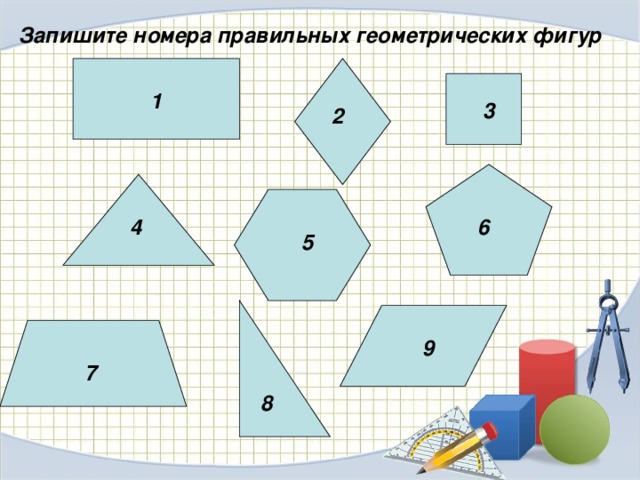
Запишите номера правильных геометрических фигур

1

3

2

4

6

5

9

7

8

V

Я это знаю

+

1.

2.

3.

4.

Новая информация для меня

-

1.

2.

3.

4.

Я думал по - другому

?

1.

2.

3.

4.

Нужны объяснения

1.

2.

3.

4.

Даны разные развертки геометрических фигур.

Задача – собрать пространственные фигуры и изучить из каких многоугольников состоит геометрическое тело.

пирамида

параллелепипед

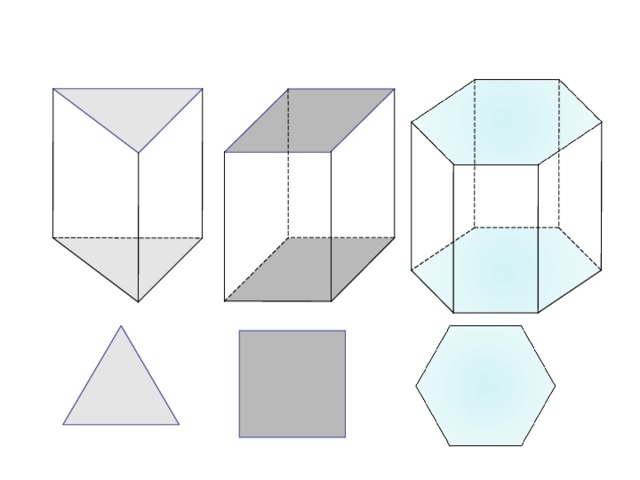
Тема урока:

«Призма»

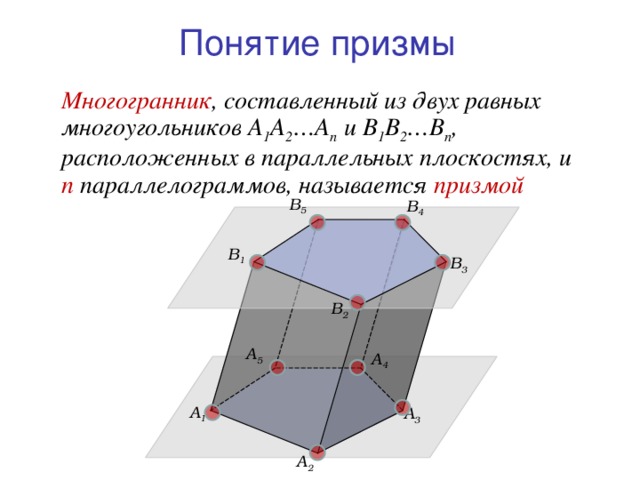
Понятие призмы

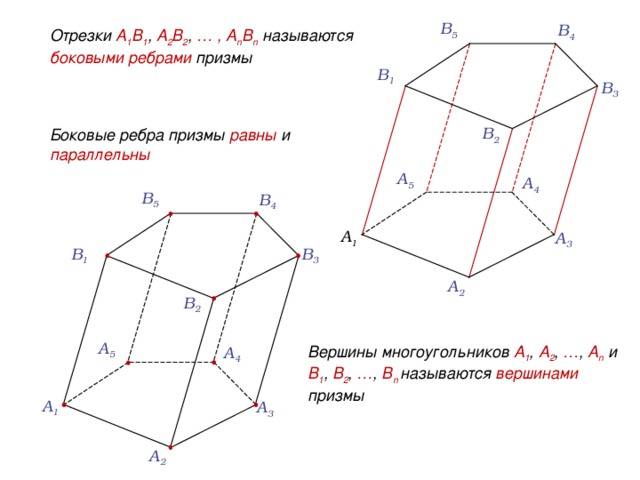
Многогранник , составленный из двух равных многоугольников A 1 A 2 …A n и B 1 B 2 …B n , расположенных в параллельных плоскостях, и n параллелограммов, называется призмой

В 5

В 4

В 1

В 3

В 2

A 5

A 4

A 1

A 3

A 2

В 5

В 4

Отрезки A 1 B 1 , A 2 B 2 , … , A n B n называются боковыми ребрами призмы

В 1

В 3

В 2

Боковые ребра призмы равны и параллельны

A 5

A 4

В 5

В 4

A 1

A 3

В 1

В 3

A 2

В 2

A 5

Вершины многоугольников A 1 , A 2 , … , A n и B 1 , B 2 , … , B n называются вершинами призмы

A 4

A 1

A 3

A 2

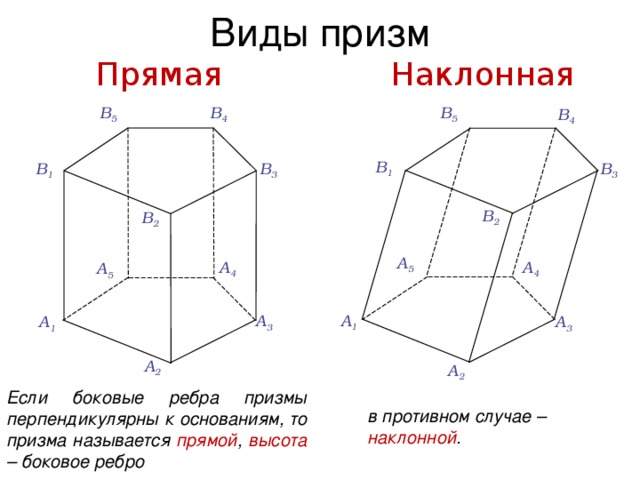
Виды призм

Прямая

Наклонная

В 4

В 5

В 5

В 4

В 1

В 3

В 3

В 1

В 2

В 2

A 5

A 4

A 4

A 5

A 1

A 3

A 1

A 3

A 2

A 2

Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой , высота – боковое ребро

в противном случае – наклонной .

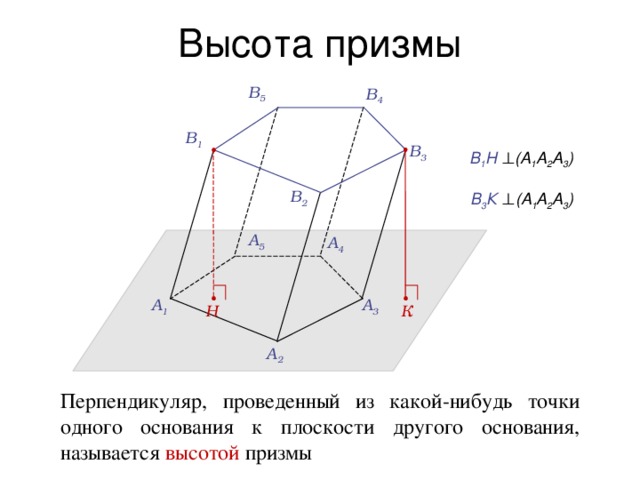
Высота призмы

В 5

В 4

В 1

В 3

В 1 Н (А 1 А 2 А 3 )

В 2

В 3 К (А 1 А 2 А 3 )

A 5

A 4

A 3

A 1

К

Н

A 2

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы

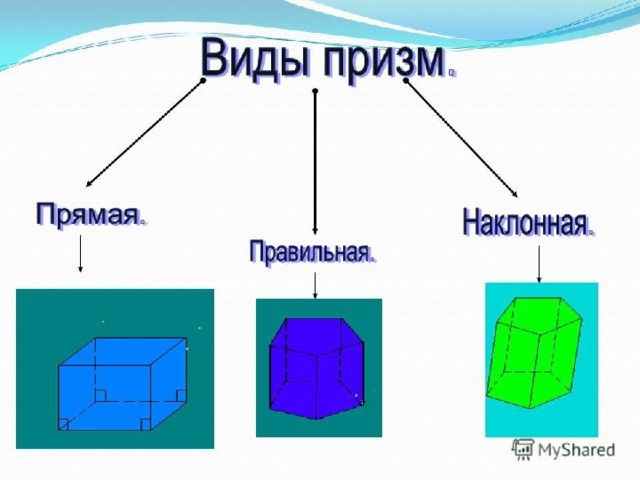
Правильная призма

В 5

В 4

В 3

В 1

В 2

A 5

A 4

A 3

A 1

A 2

Прямая призма называется правильной , если её основания – правильные многоугольники

У правильной призмы все боковые грани – равные прямоугольники

Использование призмы для творческих фотоэффектов

Оптика, электронная техника.

(очки, бинокли, объективы, телефоны)

Применение призм в лечении косоглазия

Принцип тренировки состоит в попеременном приставлении к тренируемым глазам на определенное время положительных сферо – призматических элементов различной сферической и призматической диоптрийности.

Графически это выглядит следующим образом:

Архитектура

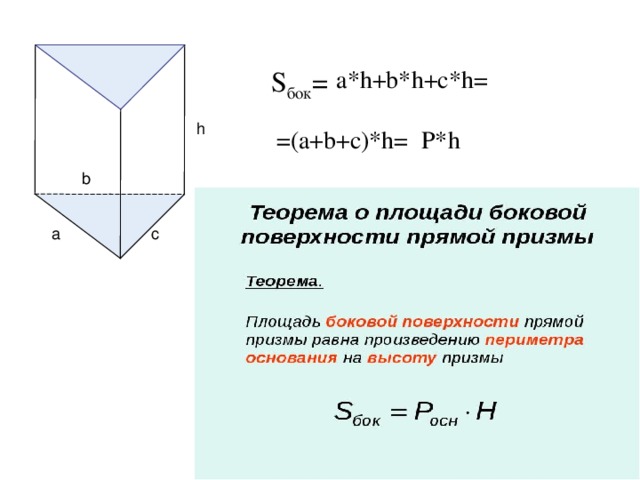
S бок =

a*h+b*h+c*h=

h

=(a+b+c)*h=

P*h

b

Интересные факты о призме

Задумывались ли вы над таким интересным фактом, что призмой может быть не только, геометрическое тело, но и другие окружающие нас предметы. Даже обычная снежинка в зависимости от температурного режима может превратиться в ледяную призму, приняв форму шестигранной фигуры.

А вот кристаллы кальцита обладают таким уникальным явлением, как распадаться на осколки и приобретать форму параллелепипеда. И что самое удивительное, на какие бы мелкие части не дробили кристаллы кальцита, результат всегда одинаковый, они превращаются в махонькие параллелепипеды.

Оказывается, призма получила популярность не только в математике, демонстрируя свое геометрическое тело, но и в области искусства, так как она является основой картин, созданных такими великими художниками, как П.Пикассо, Брак, Грисс и других.

Задание на дом:

• по учебнику п.30. ;

• на выбор несколько проектов на темы:

1. Связь призмы с другими науками.

2. Призма из букета Платона.

3. Интересные факты о призме.

V

Я это знаю

+

1.

2.

3.

4.

Новая информация для меня

-

1.

2.

3.

4.

Я думал по - другому

?

1.

2.

3.

4.

Нужны объяснения

1.

2.

3.

4.