Презентация к уроку геометрии "Признак перпендикулярности двух плоскостей"

Перпендикулярность плоскостей

Л.С. Атанасян. Геометрия 10-11.

Высшее проявление духа — это разум. Высшее проявление разума — это геометрия…

И. Ф. Шарыгин

ГЕОМЕТРИЯ и ГЕОГРАФИЯ

восхождение по отвесной стене недалеко от французского Гренобля.

Отвесная скала в Европе

В районе Ленских столбов

Меловые скалы в Англии

Удивительные отвесные  скалы  коммуны Этрета находятся на так называемом Известняковом  побережье  ( Па-де-Ко ).

Скала Прекестулен — известнейшая природная достопримечательность Норвегии

Самый высокий отвесный скальный обрыв в Крыму.

Удали лишнее высказывание и подумай, по какому принципу остальные можно разбить на две группы

Получим

• I группа:
• II группа:
• Какого высказывания не хватает?

• Плоскость β перпендикулярна плоскости γ

Поведём разговор о перпендикулярности двух плоскостей

Определение: Две плоскости называются перпендикулярными, если угол между ними прямой.

90°

Рассмотрим примеры строгого соблюдения перпендикулярности плоскостей в практической деятельности

Л.С. Атанасян «Геометрия 10-11»

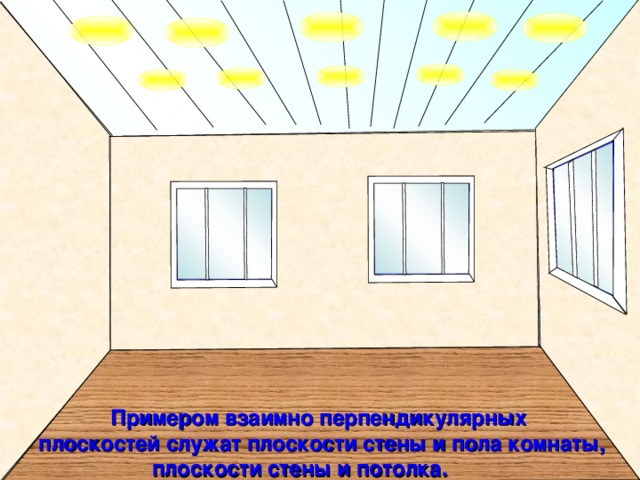
Примером взаимно перпендикулярных плоскостей служат плоскости стены и пола комнаты,

плоскости стены и потолка.

18

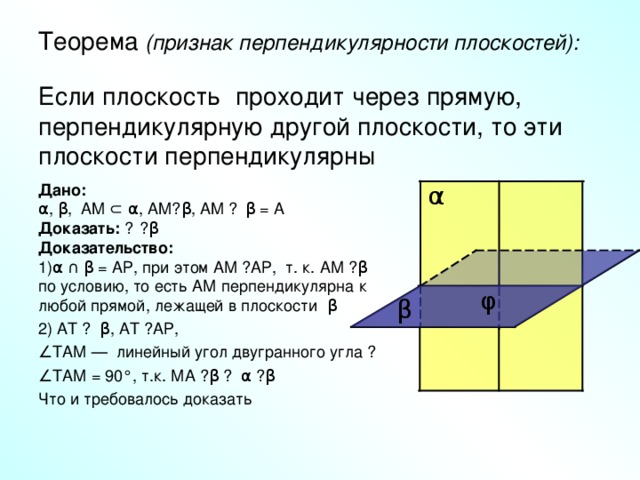
Теорема (признак перпендикулярности плоскостей): Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны

Дано:

α , β , AM ⊂ α , AM⏊ β , AM ∩ β = A

Доказать: α ⏊ β

Доказательство:

1)α ∩ β = АР, при этом АМ ⏊ АР, т. к. АМ ⏊ β

по условию, то есть АМ перпендикулярна к

любой прямой, лежащей в плоскости β

2) АТ ⊂ β, A Т ⏊ A Р,

∠ ТАМ — линейный угол двугранного угла ⇒

∠ ТАМ = 90°, т.к. МА ⏊ β ⇒ α ⏊ β

Что и требовалось доказать

α

φ

β

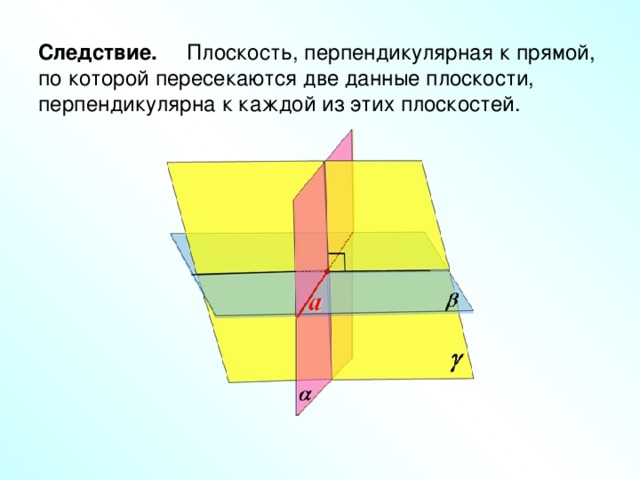
Следствие. Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.

Подумай и ответь:

• 1. Верно ли, что две плоскости, перпендикулярные третьей, параллельны?
• 2. Сколько плоскостей, перпендикулярных данной плоскости, можно провести через данную прямую?
• 3. Плоскость α перпендикулярна плоскости β . Будет ли всякая прямая плоскости α перпендикулярна плоскости β ?
• 4. Плоскость и прямая параллельны. Верно ли утверждение о том, что плоскость, перпендикулярная данной плоскости, перпендикулярна и данной прямой?
• 5. Плоскость и прямая параллельны. Будет ли верно утверждение о том, что плоскость, перпендикулярная прямой, перпендикулярна и данной плоскости?

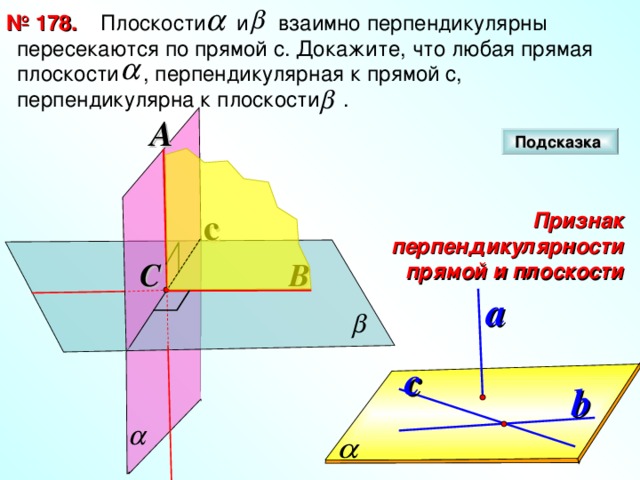
Плоскости и взаимно перпендикулярны пересекаются по прямой с. Докажите, что любая прямая плоскости , перпендикулярная к прямой с, перпендикулярна к плоскости .

№ 1 7 8.

A

Подсказка

c

Признак перпендикулярности прямой и плоскости

B

C

a

c

b

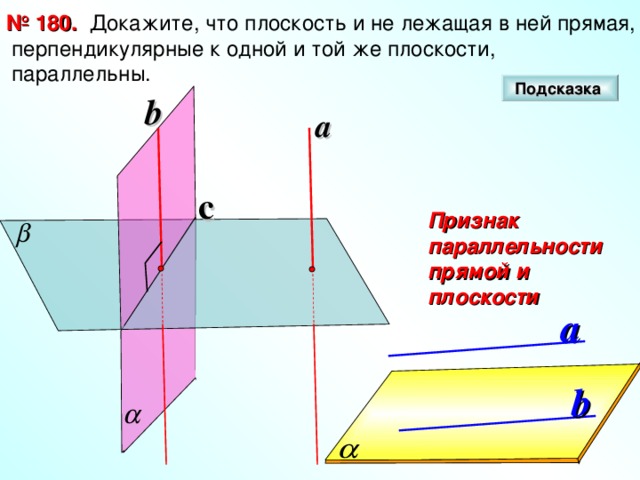
Докажите, что плоскость и не лежащая в ней прямая, перпендикулярные к одной и той же плоскости, параллельны.

№ 180.

Подсказка

b

a

c

Признак параллельности прямой и плоскости

a

b

№ 181.

Плоскости и пересекаются по прямой а. Из точки М проведены перпендикуляры МА и МВ соответственно к плоскостям и . Прямая а пересекает плоскость АМВ в точке С. Докажите, что МС а.

А

М

a

С

В

Плоскости и взаимно перпендикулярны пересекаются по прямой a . Из точки М проведены перпендикуляры МА и МВ к этим плоскостям. Прямая а пересекает плоскость АМВ в точке С. Докажите, что четырехугольник АСВМ – прямоугольник.

№ 18 2 .

М

А

a

С

В

№ 183.

Плоскости и пересекаются по прямой a и перпендикулярны к плоскости . Докажите, что прямая а перпендикулярна к плоскости .

a