Презентация к уроку геометрии "Теорема косинусов" 9 класс

Тема урока:

«Теорема

косинусов»

Выполнила : Усимова Дарья Юрьевна

База практики: МАОУ «Вадская СОШ»

2016 г.

Тест - разминка

1. sin( 90⁰ - α) =

1) cosα

2. cos(90⁰ - α) =

1) cosα

3. sin(180⁰- α) =

2) sinα

1) cosα

3) - cosα

4. cos(180⁰ - α) =

2) sinα

1) cosα

2) sinα

4) - sinα

3) - cosα

3) - cosα

4) - sinα

2) sinα

4) - sinα

3) - cosα

5. cos60⁰

4) - sinα

6. cos30⁰

7. cos45⁰

8. sin60⁰

9. sin30⁰

10. sin45⁰

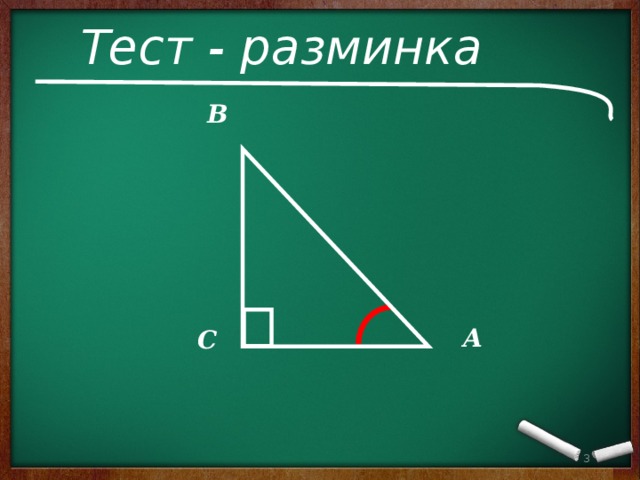
Тест - разминка

B

А

С

3

Эпиграф к уроку

«Мало знать, надо и применять.

Мало очень хотеть, надо и делать»

А. Кларк

3

3

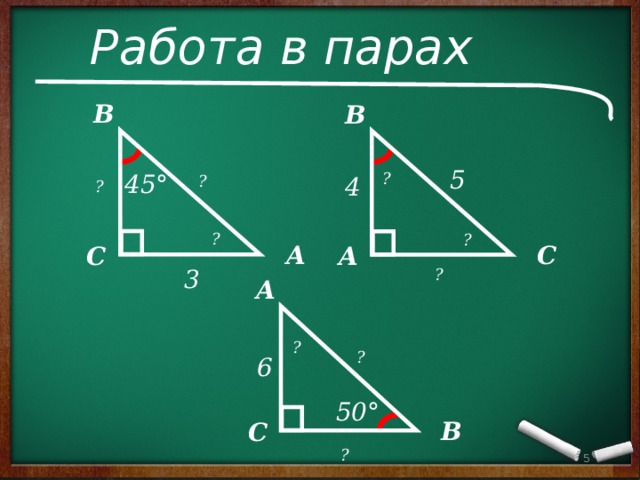
Работа в парах

B

B

5

45°

?

4

?

?

?

?

А

С

С

А

3

?

А

?

?

6

50°

В

С

?

3

5

Работа в парах

А

В

?

4

10

?

?

60°

40°

В

С

С

А

?

10

5

Цель урока

развить пространственное воображение и логическое мышление путем изучения теоремы косинусов и применения этих знаний при решении задач

Теорема косинусов

Теорема:  

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними

6

Теорема косинусов

В ( с*cosα;с*sinα )

AB = c,

AC = b,

CB = a,

∠ CAB = α

с

а

α

b

А (0;0) С ( b;0)

a 2 = (b – c*cosα) 2 +c 2 sin 2 α

a 2 = b 2 –2bc*cosα+ c 2 cos 2 α+ c 2

sin 2 α = b 2 –2bc*cosα+ c 2 (cos 2 α+ sin 2 α)

sin 2 α = b 2 –2bc*cosα+ c 2

a 2 = b 2 + c 2 –2b* cosα

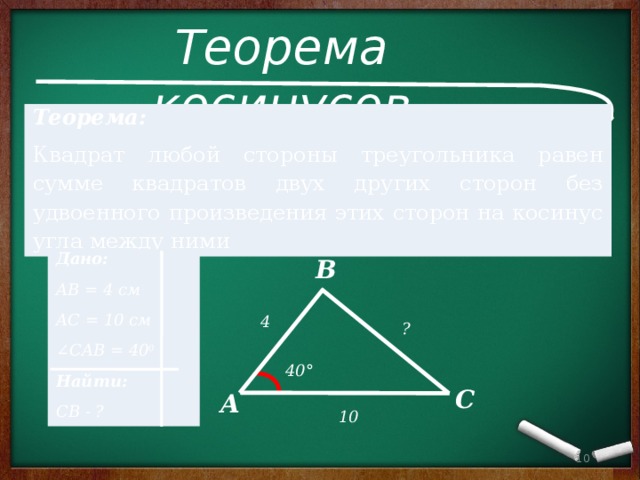
Теорема косинусов

Теорема:  

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними

Дано:

АВ = 4 см

АС = 10 см

∠ CAB = 40 0

Найти:

СВ - ?

В

4

?

40°

С

А

10

0, то треугольник остроугольный; Если cosα = 0, то треугольник прямоугольный; Если cosα " width="640"

Практическая работа

Вывод:

Для определения вида треугольника (остроугольный, прямоугольный, тупоугольный) необходимо:

1.Вычислить косинус угла, лежащего напротив большей стороны;

2. Если cosα 0, то треугольник остроугольный;

Если cosα = 0, то треугольник прямоугольный;

Если cosα

a 2  + b 2 , то треугольник тупоугольный. с b а а b b а с с " width="640"

Практическая работа

Пусть с – наибольшая сторона

1.если с 2   2  + b 2 , то треугольник остроугольный;  2.если с 2  = a 2  + b 2 , то треугольник прямоугольный;  3.если с 2   a 2  + b 2 , то треугольник тупоугольный.

с

b

а

а

b

b

а

с

с

Решение задач

№ 1025 (е)

С помощью теорем синусов и косинусов решите треугольник АВС,

если ∠С = 54 0 , а = 6,3, b = 6,3

В

6,3

54°

А

С

6,3

13

Самостоятельная работа

13

13

Подведение итогов

1. Сегодня на уроке

я изучил…

2. Я научился…

3. У меня возникли трудности с…

4. Мне хотелось бы…

13

13

Домашнее задание

• §1, п.98

Выучить теорему косинусов и ее доказательство

• Решить: № 1025 (ж, з)
• Творческое домашнее задание:

«Придумать жизненную задачу, при решении которой необходимо применить теорему косинусов»

• Реферат на тему: «Теорема косинусов в науках» (дополнительное домашнее задание, выполняется пожеланию учащихся)

13

13