Презентация к уроку математики 11 класса "Метод интервалов"

Подготовка

к ЕГЭ

Часть 2

№ 15

Часть 2

№ 15

Типовые тестовые задания ЕГЭ 2016

Вариант 1

Часть 2

№ 15

Типовые тестовые задания ЕГЭ 2016

Вариант 2

Спецификация

Спецификация КИМ ЕГЭ 2016 г. МАТЕМАТИКА, 11 класс

Федеральная служба по надзору в сфере образования и науки Российской Федерации

Обобщенный план варианта КИМ ЕГЭ 2016 года

по МАТЕМАТИКЕ

№

Проверяемые

15

Коды проверяемых требований

Уметь решать уравнения и

требования

Коды проверяемых элементов

2.3

(умений) (по КТ)

(умения)

неравенства

Уровень сложности задания

2.1, 2.2

содержания (по КЭС)

Максимальный балл

П

Примерное время выполнения

2

за выполнение задания

Примерное время выполнения

30

задания учащимся, изучавшим

задания учащимся, изучавшим

15

математику на базовом уровне,

математику на профильном

в минутах

уровне, в мин

Кодификатор

Кодификатор требований к уровню подготовки выпускников

образовательных организаций для проведения

единого государственного экзамена по МАТЕМАТИКЕ

Код раздела

Код контролируемого требования

2. Уметь решать уравнения и неравенства

(умения)

Требования (умения), проверяемые

2.3

заданиями экзаменационной работы

Решать рациональные, показательные и логарифмические

неравенства, их системы

Кодификатор элементов содержания по МАТЕМАТИКЕ

для составления контрольных измерительных материалов

для проведения единого государственного экзамена

Код раздела

Код контролируемого элемента

2.

Элементы содержания, проверяемые заданиями экзаменационной работы

Уравнения и неравенства

2.2

Неравенства

2.2.1 Квадратные неравенства

2.2.2 Рациональные неравенства

2.2.3 Показательные неравенства

2.2.4 Логарифмические неравенства

2.2.5 Системы линейных неравенств

2.2.6 Системы неравенств с одной переменной

2.2.7 Равносильность неравенств, систем неравенств

2.2.8 Использование свойств и графиков функций при решении неравенств

2.2.9 Метод интервалов

2.2.10 Изображение на координатной плоскости множества решений неравенств с двумя переменными и их систем

Экспресс подготовка

видео уроки

0; f (x) ≥ 0; f (x) Свойство непрерывной функции помогает обосновать метод интервалов для решения неравенств. «Корни непрерывной функции (f (х) = 0) разбивают ось х на промежутки, внутри которых функция сохраняет постоянный знак» " width="640"

Метод интервалов

для решения

неравенств вида

f (x) 0; f (x) ≥ 0; f (x)

Свойство непрерывной функции помогает обосновать метод интервалов для решения неравенств.

«Корни непрерывной функции (f (х) = 0) разбивают ось х на промежутки, внутри которых функция сохраняет постоянный знак»

Алгоритм решения неравенств

методом интервалов

На примере:

• Разложить на множители числитель и знаменатель функции.
• Найти точки разрыва функции и её нули.
• Нанести точки разрыва и нули на ось х.
• Выделить промежутки оси х, на которые разбилась область определения функции отмеченными точками.

• Найти знак функции на каждом из интервалов. Для этого надо определить знак функции в какой либо одной точке этого интервала . По свойству непрерывной функции в каждом из интервалов функция сохраняет постоянный знак.

• Выделить необходимые промежутки и записать ответ.

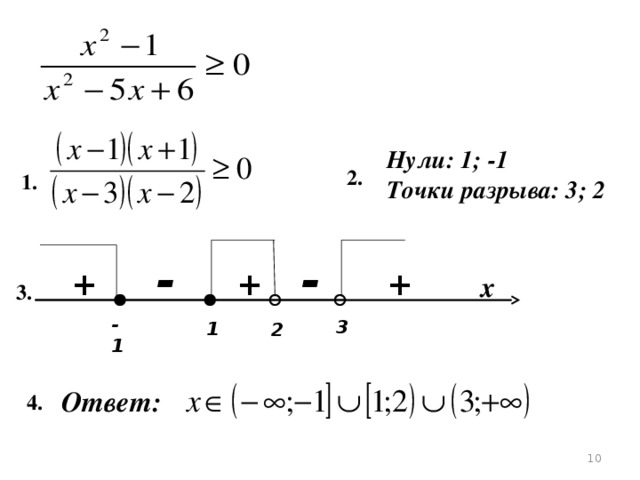
Нули: 1; -1

Точки разрыва: 3; 2

2.

1.

-

-

+

+

+

х

3.

-1

3

1

2

Ответ:

4.

Замечания,

позволяющие упростить решение неравенств методом интервалов и сэкономить время на выполнение заданий

Замечания:

1. Для решения неравенств f (х)≥≤0, где f (х) – непрерывная функция, методом интервалов, необходимо знать корни этой функции. Полезно начинать с разложения левой части на множители.

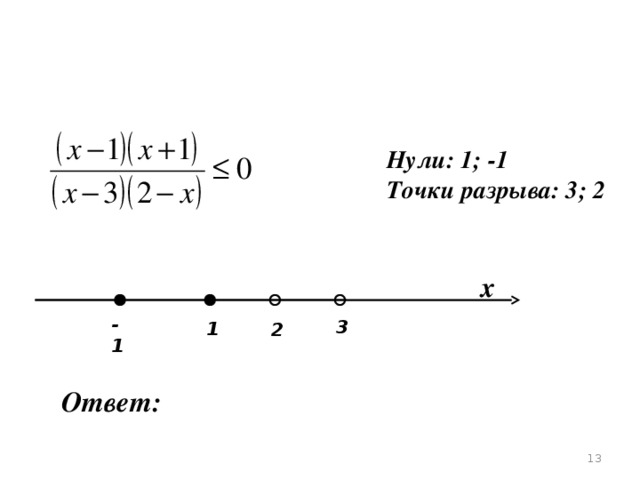
Нули: 1; -1

Точки разрыва: 3; 2

х

-1

3

1

2

Ответ:

Замечания:

2. Если в разложении остались лишь линейные двучлены, то нужно записать их в виде (х – а) (а не (а - х)). Отметить на оси х корни функции, поставить на крайнем правом промежутке знак «+» и, двигаясь справа налево, чередовать знаки .

Чтобы представить f (х) в виде (х – а 1 ) (х – а 2 )… (х – а n ) в случае необходимости умножить обе части неравенства на «- 1», изменив знак неравенства на противоположный.

Задания

Решить неравенство:

(1 – х 2 )(х 3 – 1)(х 4 – 1) ≤ 0

Замечания:

3. Если при этом в разложении окажутся квадратные трехчлены с D то их из разложения можно отбросить , т.к. они будут всюду положительны и не будут влиять на знак f (х).

Замечания:

4. Если в разложении линейные двучлены, стоят в чётной степени, то при «переходе» через нуль этого двучлена знак функция не меняет.

Замечания:

5. Если дано нестрогое неравенство, то следует не забыть включить в ответ те значения х из отброшенных, в которых f (х) = 0.

Задания

Решить неравенство:

Задания

Решить неравенство:

Замечания:

6. Если точка разрыва и нуль функции совпадают , то в полученный промежуток эта точка не включается , т.к. не входит в ОДЗ.