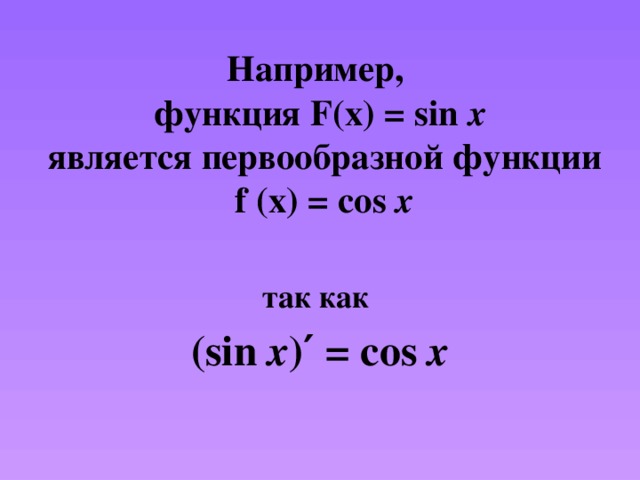Презентация к уроку по теме "Первообразная"

Первообразная

Разработала преподаватель математики высшей квалификационной категории Бердского политехнического колледжа

Кулинич Татьяна Андреевна

• «Сближение теории с практикой дает самые благотворные результаты, и не одна только практика от этого выигрывает, сами науки развиваются под влиянием ее, она открывает им новые предметы для исследования, или новые стороны в предметах давно известных.»

П.Л. Чебышёв

Цели урока

• Образовательная :  ввести определение первообразной; установить связь между производной и первообразной; сформировать умение проверять, является ли данная функция первообразной для другой, заданной на некотором числовом промежутке.
• Развивающая : формирование логических приемов мыслительной деятельности, познавательной активности и самостоятельности.
• Воспитательная : формирование интереса к изучению математики, развитие устойчивой мотивации к учебной деятельности, воспитание познавательной активности.

Актуальность темы

• Первообразная – одно из важнейших понятий математики, возникшее в связи с потребностью, с одной стороны, отыскивать функции по их производным (например, находить функцию, выражающую путь, пройденный движущейся точкой, по скорости этой точки), а с другой – измерять площади, объемы, длины дуг, работу сил за определенный промежуток времени и т. п.

Определение первообразной

Функция F называется первообразной для функции f на заданном промежутке, если для всех х из этого промежутка

F ′(х) = f(х)

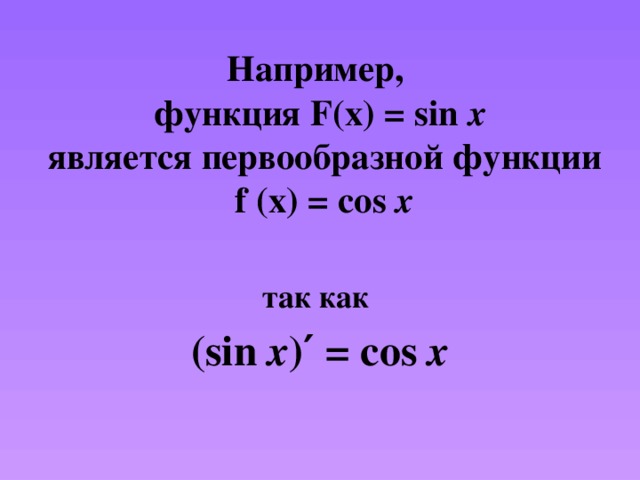
Например, функция F(х) = sin x является первообразной функции f (x) = cos x

так как

(sin x ) ′ = cos x

Функция F(x) = х ⁴ /4 +5 есть первообразная для функции f(x)=x³

так как

F ′(x) = (х⁴ /4 +5)′ = 4x³/4 = x³

• Если F(x) – первообразная для функции f(x) на некотором промежутке, то функция F(x)+C также является первообразной функции f(x) на этом промежутке, где C –произвольная постоянная.

Таблица первообразных

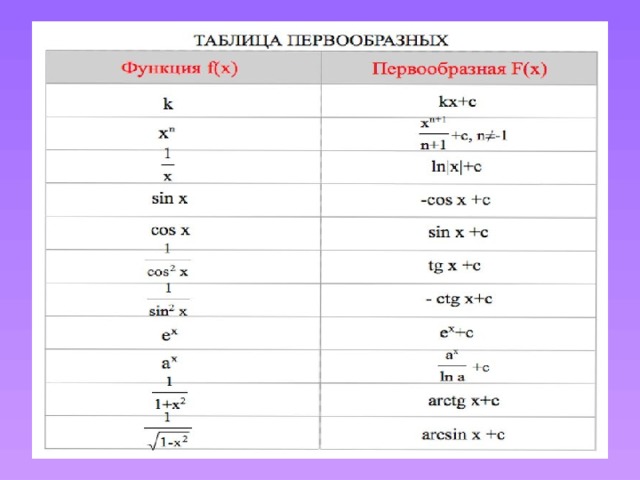
Правила нахождения первообразных

Правило 1

• Если F есть первообразная для f,

а G – первообразная для g,

то F + G есть первообразная для

f + g.

• Первообразная суммы равна сумме первообразных

Правило 2

• Если F есть первообразная для f,

а k – постоянная,

то kF есть первообразная для kf

Постоянный множитель можно выносить за знак первообразной

Правило 3

• Если F(x) есть первообразная для f(x), а k и b – постоянные, причем k ≠0, то

1/k • F(kx + b)

есть первообразная для функции

f(kx + b)

Образцы решения

Найдите общий вид первообразных для функций:

1. f(х) = х ³ - х⁴

Решение

F(х) =¼х⁴ - ⅕х⁵ + С

(Правило 1)

Найдите общий вид первообразных для функций:

2. f(х) = 5cos x

Решение

F(х) = 5sin x + C

(Правило 2)

Найдите общий вид первообразных для функций:

1. f(х) = sin4x

Решение

F(х) =¼(-cos4x) + C

(Правило 3)

Итоги урока

• Никто еще не воспевал В достойных рифмах интеграл, И даже дифференциал В стихи ни разу не попал. А синус! Сколько страсти в нем… Итак, попробуем, начнем. Тема урока целесообразная –  искали мы первообразную Задача была ясная – найти первообразную У доски стояли – интегрирование изучали Функция обратная простая и понятная Она такая разная – эта первообразная Для кого работа неподвластная найти первообразную?

Литература

• 1. Учебник «Алгебра и начала анализа» 10-11 классы. Автор А.Г. Мордкович, 2016 год
• Задачник «Алгебра и начала анализа» 10-11 классы. Авт.: А.Г. Мордкович, Л.О. Денищева, 2016 год
• Методическое пособие для учителя «Алгебра и начала анализа» 10-11 классы. Автор А.Г. Мордкович
• Математика. Алгебра и начала математического анализа, геометрия. УМК для старшей школы: 10 – 11 классы (ФГОС). Методическое пособие для учителя. Базовый уровень Авторы:  Шихова Н. А., Кузнецова М. В. Год издания:  2013
• Первообразная http://www.yaklass.ru/materiali