Презентация к уроку по теме "Площадь трапеции"

Урок геометрии 8 класс

Проверка домашнего задания

№ 476

Докажите, что площадь ромба равна половине произведения его диагоналей.

Дано: В Доказательство:

АВСD- ромб Диагональ делит ромб АВСD на

Доказать: два треугольника АВС и АСD

S ABCD = 1/2 ·AC·BD А С S ABC = 1/2·AC·BO , S ADC =1/2 ·AC·DO

S ABCD = S ABC + S ADC =

1/2·AC·BO + 1/2·AC·DO =

D 1/2·AC·(BO + DO) =1/2·AC·BD

Решение:

А) ½ · 32 см · 14 см = 224 см 2

Б) ½ · 4,6 дм · 2 дм = 4,6 дм 2

Проверка домашнего задания

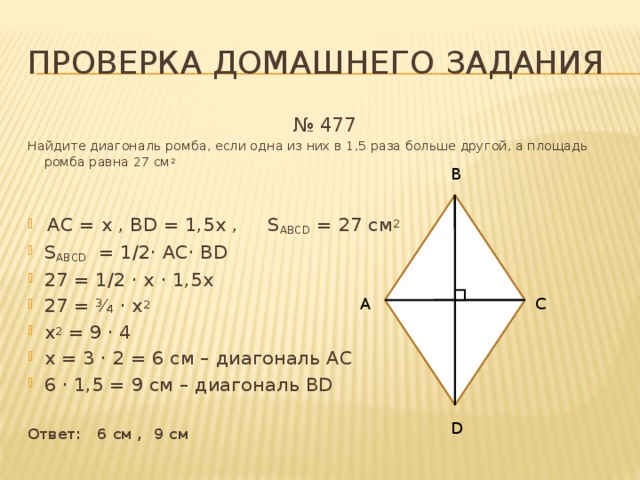
№ 477

Найдите диагональ ромба, если одна из них в 1,5 раза больше другой, а площадь ромба равна 27 см 2

• АС = х , ВD = 1,5х , S ABCD = 27 см 2
• S ABCD = 1/2· АС· ВD
• 27 = 1/2 · х · 1,5х
• 27 = ¾ · х 2
• х 2 = 9 · 4
• х = 3 · 2 = 6 см – диагональ АС
• 6 · 1,5 = 9 см – диагональ ВD

Ответ: 6 см , 9 см

В

А

С

D

Проверка домашнего задания

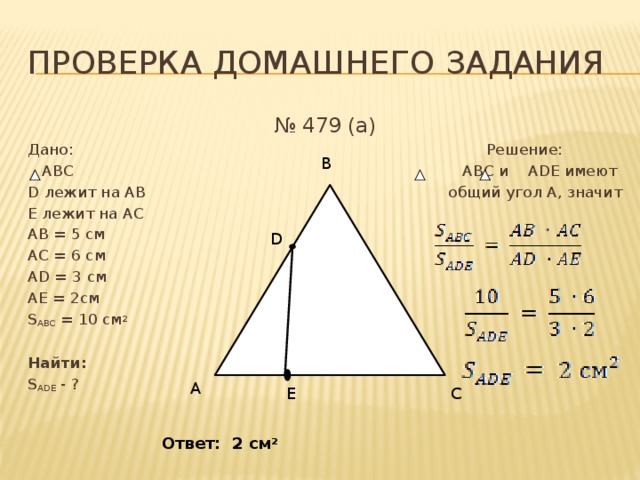
№ 479 (а)

Дано: Решение:

АВС АВС и АDЕ имеют

D лежит на АВ общий угол А, значит

Е лежит на АС

АВ = 5 см

АС = 6 см

АD = 3 см

АЕ = 2см

S ABC = 10 см 2

Найти:

S ADЕ - ?

В

D

А

E

С

Ответ: 2 см 2

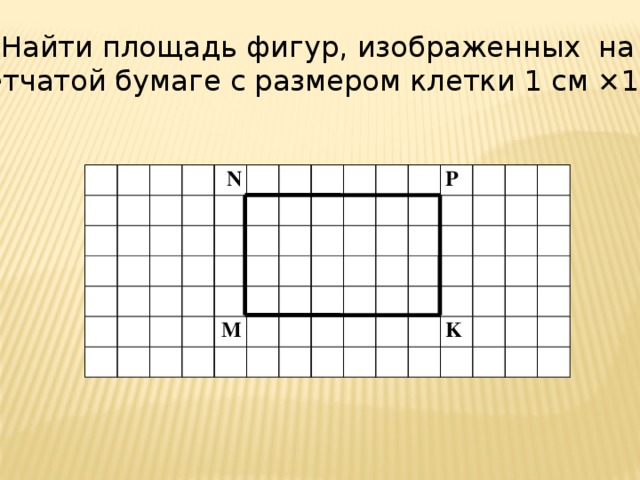
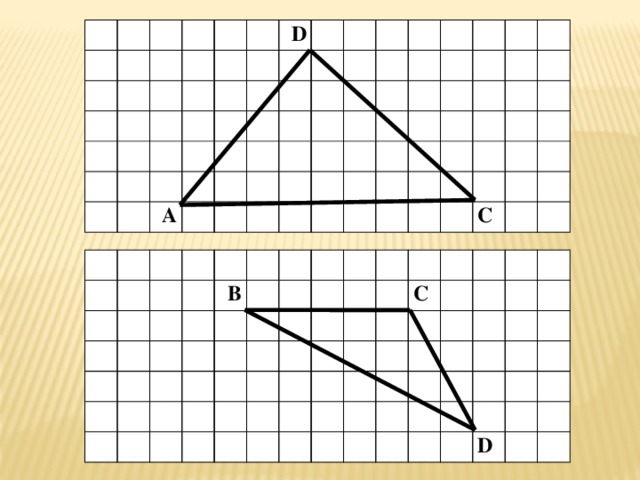
Найти площадь фигур, изображенных на

клетчатой бумаге с размером клетки 1 см ×1 см

N

M

P

K

В

А

С

D

T

S

R

O

D

A

C

B

C

D

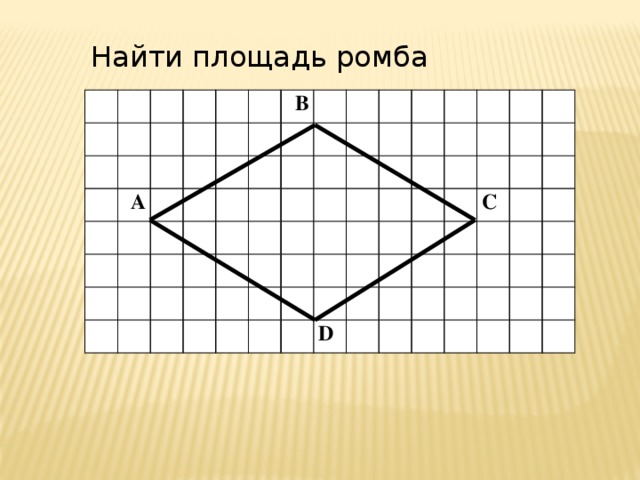
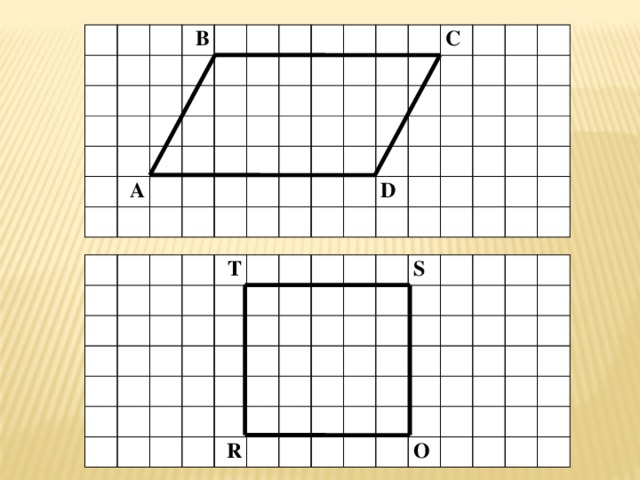
Найти площадь ромба

А

В

D

С

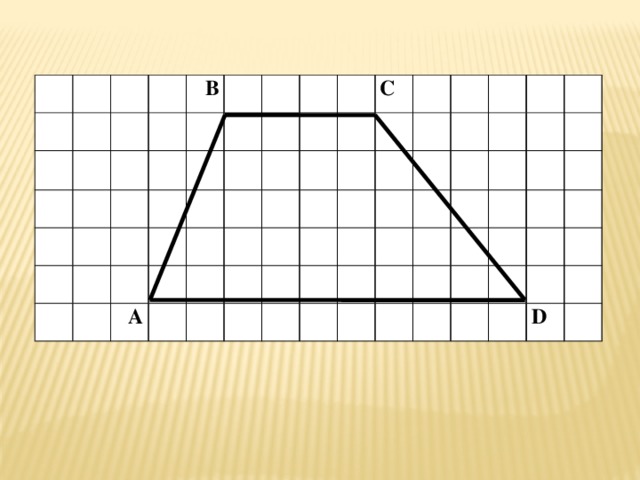
B

A

C

D

Цели урока

• Открыть теорему о площади трапеции и показать ее применение в процессе решения задач
• Совершенствовать навыки решения задач

B

A

C

H

O

D

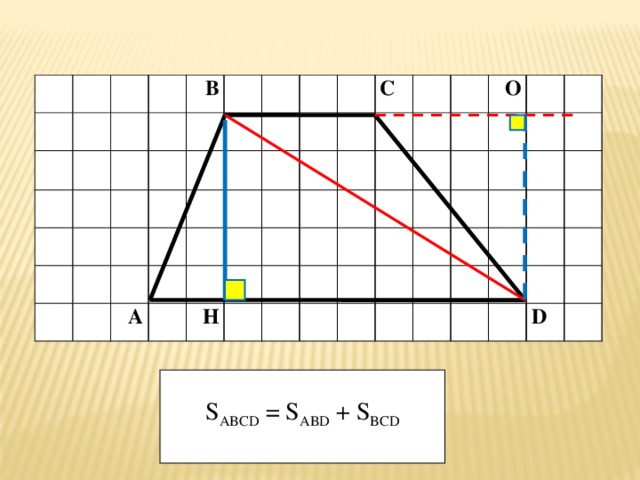
S ABCD = S ABD + S BCD

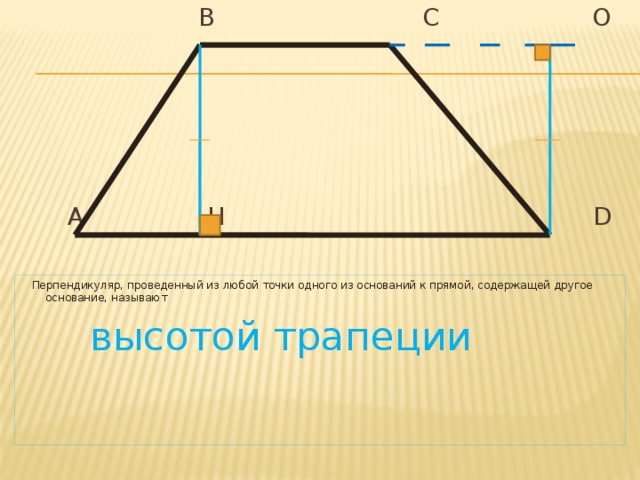
В С O

А Н D

Перпендикуляр, проведенный из любой точки одного из оснований к прямой, содержащей другое основание, называют

высотой трапеции

Задача: Найти площадь трапеции АВСD с основаниями ВC и

AD и высотой ВН.

Дано:

АВСD – трапеция

ВC и AD – основания

ВН – высота

Найти:

S ABCD - ?

Задача: Найти площадь трапеции АВСD с основаниями ВC и

Дано:

AD и высотой ВН.

АВСD – трапеция

ВC и AD – основания

ВН – высота

Найти:

B C O

S ABCD - ?

А H D

Решение:

• Проведем диагональ ВD и вторую высоту трапеции DO.
• S ABCD = S ABD + S BCD
• S ABD = 1/2 ·AD·BH , S BCD =1/2 ·BC ·DO
• HBOD- прямоугольник ,то BH=DO.
• S ABCD = 1/2 ·AD·BH + 1/2 ·BC ·DO

=1/2 ∙(AD+BC) ∙ BH.

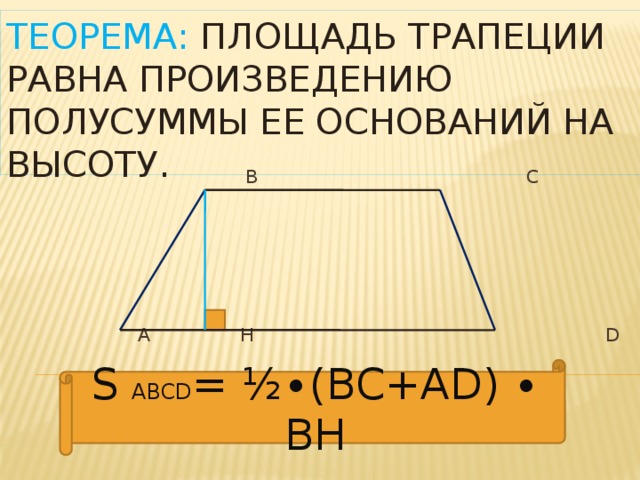
Теорема: Площадь трапеции равна произведению полусуммы ее оснований на высоту.

В С

А Н D

S ABCD = ½∙(BC+AD) ∙ ВН

S трапеции = ½ ∙ (а + b)∙ h,

где a и b – основания трапеции,

h - высота

B

A

C

D

Решите задачу

• Задача 1:

• Задача 2:

Найти площадь трапеции, если ее основания равны 5 см и 7 см, а высота 10 см.

Найти высоту трапеции, если ее основания равны 4 см и 8 см, а площадь 72 см 2 .

60 см 2

12 см

Учебник (письменно)

№ 480 (б)

Дано: АВСD-трапеция,

АВ и CD – основания,

Найти: S ABCD.

Решить самостоятельно

• 1 вариант - № 480 (а)

• 2 вариант - № 480 (в)

Найдите площадь трапеции

Найдите площадь трапеции

АВСD c основаниями АВ и CD, если:

АВСD c основаниями АВ и CD, если:

АВ=21 см, СD =17 см, высота BH =7 см.

АВ=5 см, СD =13 см,

• S=1/2∙(21+17) ∙ 7=

BC ⊥AB, BС =8 см.

• S=1/2∙(13+5) ∙ 8 =

133

72

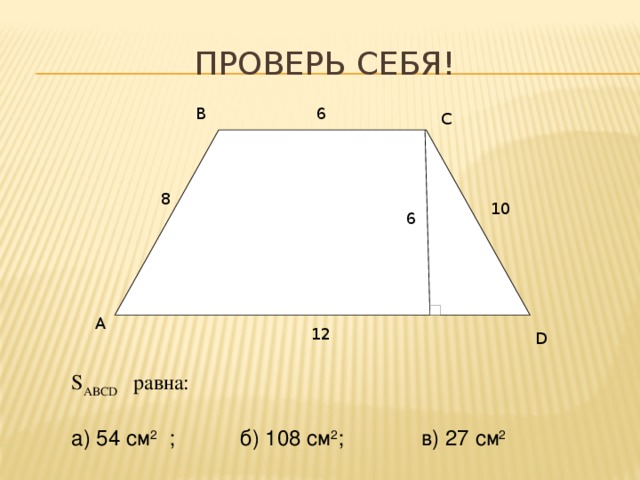
Проверь себя!

6

В

С

8

10

6

А

12

D

S ABCD равна:

а) 54 см 2 ; б) 108 см 2 ; в) 27 см 2

Итог урока

• Какая проблема возникла у нас в начале урока при решении задач по готовым чертежам?

• Как вы считаете, данную проблему мы решили на сегодняшнем уроке?

• Как найти площадь трапеции?

• Какие знания нам пригодились при выполнении заданий на уроке?

Домашнее задание

• П. 53
• № 482,
• № 518 (а)

Спасибо за внимание!

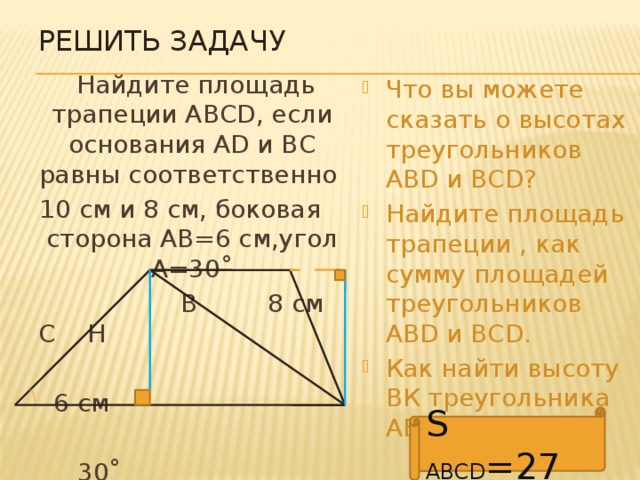
Решить задачу

Найдите площадь трапеции АВСD, если основания AD и ВС равны соответственно

10 см и 8 см, боковая сторона АВ=6 см,угол А=30˚

В 8 см С Н

6 см

30˚

А К 10 см D

• Что вы можете сказать о высотах треугольников АВD и BCD?
• Найдите площадь трапеции , как сумму площадей треугольников АВD и BCD.
• Как найти высоту ВК треугольника АВD?

S ABCD =27