Презентация к уроку по теме: Застосування похідної до дослідження функцій

« Застосування похідної до дослідження функцій »  

Мета урока:

• Систематизувати й узагальнити вміння та знання по знаходженню: а) проміжків монотонності функції; б) критичних точок; в) максимумів і мінімумів функції; г) найбільшого і найменшого значення функції. • Організувати діяльність з узагальнення застосування похідної до дослідження функцій. • Виробити вміння самостійно застосовувати знання, здійснюючи їх перенесення в нові умови. • Засвоєння знань і способів дії в комплексі .

Математичний диктант

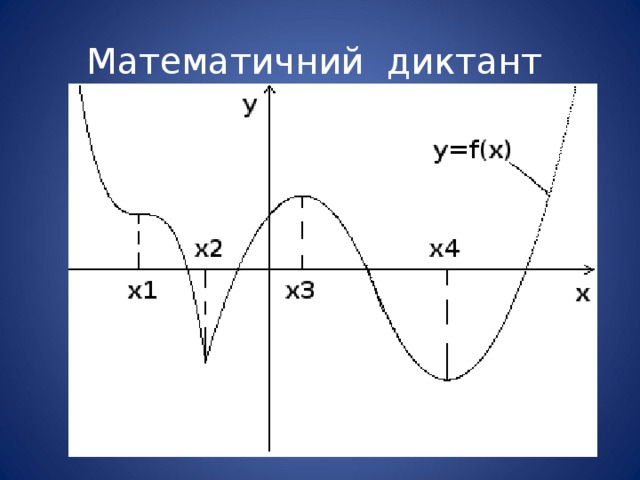
Відповіді:

• x 1 , x 2 , x 3 , x 4
• f '(x 2 ) не існує
• x 2 , x 3 , x 4
• f '(x) ≤0
• Функція зростає на [x 2 ; x 3 ] і на [x 4 ; + ∞)
• Функція спадає на і на (-∞; x 2 ] і [x 3 ; x 4 ]
• f '(x)≥ 0
• f '(x) ≤0
• х 2
• х min = x 3 , x max = x 4

Задача № 1.

При яких значеннях параметра а, рівняння x 3 -3x = a, має рівно два різних кореня?

Задача № 2.

• Знайдіть при якому значенні а, функція f (x) = - x 3 + 3x 2 +a, має max [1; 3] ⁡ f (x) = 3?