Презентация к уроку "Системы счисления"

"Мысль выражать все числа десятью знаками, придавая им кроме значения по форме еще значение по месту, настолько проста, что именно из-за этой простоты трудно понять, насколько она удивительна."

П.Лаплас

Наиболее известные нумерации мира

Древнеегипетская нумерация

Древнегреческая нумерация

Вавилонская нумерация

Нумерация индейцев Майя

Старо-Китайская нумерация

Славянская кириллическая нумерация

Славянская глаголическая нумерация

Латинская нумерация

Современная арабская нумерация

История чисел и систем счисления

«Все есть число»

Системы счисления

• Система счисления – это способ записи чисел с помощью специальных знаков – цифр .
• Числа: 123, 45678, 1010011, CXL
• Цифры(символы, участвующие в записи числа): 0, 1, 2, … I, V, X, L, …
• Алфавит – это набор цифр . {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
• Типы систем счисления:

• непозиционные – значение цифры не зависит от ее места (позиции) в записи числа; позиционные – значение цифры зависит от ее места (позиции) в записи числа;
• непозиционные – значение цифры не зависит от ее места (позиции) в записи числа;
• позиционные – значение цифры зависит от ее места (позиции) в записи числа;

СИСТЕМА СЧИСЛЕНИЯ - это способ изображения чисел и соответствующие ему правила действия над числами.

I, II, III, IV, V, VI, VII,….

1, 2, 3, 4, 5, 6, 7, 8, 9,0

Непозиционные системы счисления

Унарная система счисления

(10-11 тысяч лет до н.э.)

Унарная – одна цифра обозначает единицу (1 день, 1 камень, 1 баран, …)

На раскопках стоянок древних людей археологи находят изображения в виде засечек, черточек на твердых поверхностях: камне, глине, дереве- это так считали наши предки какие-то предметы, мешки, скот.

Древнеегипетская десятичная непозиционная система

Египетская нумерация

1. Как и большинство людей для счета небольшого количества предметов Египтяне использовали палочки.

Если палочек нужно изобразить несколько, то их изображали в два ряда, причем в нижнем должно быть столько же палочек сколько и в верхнем, или на одну больше.

10. Такими путами египтяне связывали коров

Если нужно изобразить несколько десятков, то иероглиф повторяли нужное количество раз. Тоже самое относится и к остальным иероглифам.

100. Это мерная веревка, которой измеряли земельные участки после разлива Нила.

Попробуйте узнать и прочитать это число?

2521

19*31

• 31

• 62

• 124

• 248

• 496

19=1+2+16

19*31=31+62+496=589

Нумерация индейцев Майя

1

2

3

4

5

11

12

13

14

15

6

7

8

9

10

0 или 20

Китайская нумерация

1

2

3

4

5

10

100

1000

6

7

8

9

0

°

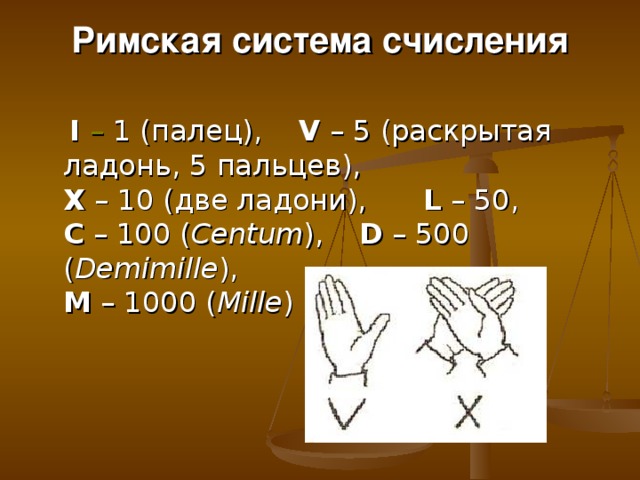
Римская система счисления

I – 1 (палец), V – 5 (раскрытая ладонь, 5 пальцев), X – 10 (две ладони), L – 50, C – 100 ( Centum ), D – 500 ( Demimille ), M – 1000 ( Mille )

Правила:

• (обычно) не ставят больше трех одинаковых цифр подряд если младшая цифра (только одна !) стоит слева от старшей, она вычитается из суммы ( частично непозиционная!)
• (обычно) не ставят больше трех одинаковых цифр подряд
• если младшая цифра (только одна !) стоит слева от старшей, она вычитается из суммы ( частично непозиционная!)

• Пример: 2381 = M M C C C L X X X I

• Записать 444 в римской системе счисления
• Записать 1986 в римской системе счисления
• Записать 2014 в римской системе счисления

• Какое число записано?
• MMIV
• LXV
• CMLXIV

Алфавитные системы счисления

Славянская глаголическая нумерация

1

2

3

4

5

6

7

8

9

100

200

300

400

500

600

700

800

900

10

20

30

40

50

60

70

80

90

1000

Вспомогательные символы для записи больших чисел

(Введены в конце XV века;

свойственны только славянам)

Тысяча – 1.000

Десятки тысяч – 10.000

Десятки тем – 100.000

Десятки легионов – 1.000.000

Десятки леодров – 10.000.000

Десятки вранов – 100.000.000

Древнерусская нумерация

«великое число»

до 10 49

«малое число»

Великое число – «коли прилучался великий счет и перечень»

• 10 6 - тьма – тысяча тысяч;
• 10 12 – легион – тьма тем;
• 10 24 – леодр – легион легионов;
• 10 48 – вран – леодр леодров;
• 10 49 – колода – десять вранов.

«И более сего несть человеческому уму разумети, токмо един бог весть»

Недостатки непозиционной системы счисления:

• Для записи больших чисел необходимо вводить новые цифры (буквы);
• Трудно записывать большие числа;
• Нельзя записывать дробные и отрицательные числа;
• Нет нуля;
• Очень сложно выполнять арифметические действия.

Позиционные системы счисления

Позиционные системы счисления

В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен. Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам; развита была такая нумерация индусами и имела неоценимые последствия в истории человеческой цивилизации.

Основные достоинства позиционной системы счисления:

• Ограниченное количество символов для записи чисел;
• Простота выполнения арифметических операций.

Основание позиционной системы счисления ( q ) – количество символов, используемых для записи числа.

Двенадцатеричная система

На Руси счет велся дюжинами, вспомните, чему равна ДЮЖИНА?

• Год – 12 месяцев, половина суток – 12 часов, сервизы и столовые приборы рассчитаны на 12 персон.

Вавилонская шестидесятеричная система

Числа в этой системе счисления составлялись из знаков двух видов:

прямой клин служил для обозначения единиц,

а лежачий клин — — для обозначения десятков.

Число 32, например, записывали так:

Знаки и служили цифрами в этой системе. Число 60 снова

обозначалось тем же знаком , что и 1, этим же знаком обозначались и числа 3600, 216000 и все другие степени 60. Поэтому вавилонская система счисления получила название шестидесятеричной .

Для определения значения числа надо было изображение числа разбить на разряды справа налево. Новый разряд начинался с появления прямого клина после лежачего, если рассматривать число справа налево.

Кто как считает

• На островах Океании используется одинадцатеричная система счисления.

• Японцы иногда используют пятеричную систему счисления.

Десятичная система

Появилась она в Индии в \/ в.н.э. и возникла она после появления цифры 0, которую придумали греческие астрономы для обозначения отсутствующей величины.

В последствии с этой системой счисления познакомились арабы. Они по достоинству оценили её, начали использовать и в ХII веке завезли в Европу. И с этого времени человечество пользуется этой системой счисления.

Десятичная 0,1,2,3,4,5,6,7,8,9

Почему именно десять?

Тот факт, что основанием используемой нами системой счисления является число 10, объясняется тем, что природа наделила нас десятью пальцами на руках и ногах.

Двоичная система

• С появлением информатики, вычислительной техники нашла свое применение 2-я система счисления, корни которой уходят в древний Китай.

Часы в двоичной системе счисления

Двоичная система счисления применяется в компьютерной технике и других технических устройствах. Используются две цифры – 0 (не сигнала)и 1 (есть сигнал).

1 0 1 1

В двоичной системе счисления для записи чисел используются всего две цифры: 0 и 1, q = 2 .

Позиционные системы счисления

Система счисления

Алфавит языка

Десятичная

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Двоичная

0, 1

Восьмеричная

0, 1, 2, 3, 4, 5, 6, 7

Шестнадцатеричная

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A (10) , B (11) , C (12) , D (13) , E (14) , F (15)

Правило.

Для перевода целого числа N в систему счисления с основанием q необходимо разделить N на q с остатком . Затем неполное частное , полученное от этого деления снова разделить на q с остатком и т.д., пока последнее частное не станет равным нулю . Получившиеся остатки выписать в обратном порядке.

Примеры:

Переведем числа 75 и 12 из десятичной системы счисления в двоичную.

• 2

1 37 2

1 18 2

0 9 2

1 4 2

0 2 2

0 1 2

1 0

12 2

0 6 2

0 3 2

1 1 2

1 0

Ответ: 12 10 = 1100 2

Ответ: 75 10 = 1001011 2

Задание.

Переведите десятичные числа в двоичную.

1 вариант - 25 и 42

2 вариант - 35 и 30

Ответы:

25 10 = 11001 2

35 10 = 100011 2

42 10 =101010 2

30 10 = 11110 2

Правило.

Для перевода правильной десятичной дроби N в систему счисления с основанием q необходимо умножить N на q, записанное в той же десятичной системе , затем дробную часть полученного произведения снова умножить на q , до тех пор пока дробная часть не станет равной нулю или не будет достигнута требуемая точность . Получившиеся результате произведения целые части дроби выписать сверху вниз .

Примеры:

Переведем число 0,1875 и 0,12 (с точностью до 6 знаков) из десятичной системы счисления в двоичную.

0 1875

0 375

0 75

1 5

1 0

0 12

0 24

0 48

0 96

1 92

1 84

1 68

… …

Ответ: 0,1875 10 = 0,0011 2

Ответ: 0,12 10 = 0,000111 2

Задание.

Переведите десятичные дробные числа в двоичную.

1 вариант - 0,25 и 0,3 (с точностью 4 знака)

2 вариант - 0,75 и 0,4 (с точностью 4 знака)

Ответы:

0,25 10 = 0,01 2

0,75 10 = 0,11 2

0,3 10 = 0,0100 2

0,4 10 = 0,0110 2

В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д.

Например:

1476 = 1000 + 400 + 70 + 6

Можно пойти еще дальше и разложить так:

1476 =1*10 3 +4 * 10 2 + 7 * 10 1 + 6 *10 0

Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:

10001001 = 1*2 7 + 0*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0

Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:

1*2 7 + 0*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137

Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:

10001001 2 = 137 10

Правило.

Для перевода числа х ( х q = а п а п-1 …а 0 ,а -1 а -2 …а -т ) из системы счисления с основанием q ( q = 2, 8 или 16 ) в десятичную систему счисления необходимо вычислить значение многочлена

х 10 = а п q п + а п-1 q п-1 + … + а 0 q 0 + а -1 q -1 + а -2 q -2 + … + а -т q -т .

Примеры:

Переведем число 111001,1 2 в десятичную систему счисления.

Решения:

111001,1 2 = 1 . 2 5 + 1 . 2 4 + 1 . 2 3 + 0 . 2 2 + 0 . 2 1 + 1 . 2 0 + 1 . 2 -1 = 57,5 10

Задание:

Переведите числа в десятичную систему счисления.

1 вариант - 1 111, 01 2

2 вариант - 10 000, 001 2

Ответы:

1 111, 01 2 = 15, 25 10

10 000, 001 2 = 16, 125 10

Домашнее задание.

• Переведите числа из десятичной системы счисления в двоичную:

100,45 99 0,8125

2. Переведите число в десятичную систему счисления:

110 000, 111 2

Ломаем голову.

Ей было 1100 лет.

Она в 101 класс ходила

В портфеле по 100 книг носила

Все это правда, а не бред.

Когда пыля десятком ног,

Она шагала по дороге,

За ней всегда бежал щенок

С одним хвостом, зато стоногий .

Она ловила каждый звук

Своими десятью ушами,

И 10 загорелых рук

Портфель и поводок держали.

И 10 темно-синих глаз

Оглядывали мир привычно.

Но станет все совсем обычным,

Когда поймете наш рассказ.

Домашнее задание:

1.Прочитать стр.96-100

В.2,3 письменно в тетрадях.

Дополнительное задание.

Переведите в двоичную.

2004 10 и 3004 10

Ответы:

2004 10 = 11 111 010 100 2

3004 10 = 101 110 111 100 2

5

2

1

7

3

4

8

6

9

к

л

а

в

и

а

т

у

р

а

д

ж

о

й

с

т

и

к

м

о

н

и

т

о

р

п

р

и

н

т

е

р

п

а

м

я

т

ь

т

ю

н

е

р

д

и

с

к

е

т

а

с

к

а

н

е

р

п

р

о

ц

е

с

с

о

р